备战蓝桥杯---动态规划的一些思想1
话不多说,直接看题:
目录
1.双线程DP
2.正难则反+多组DP
3.换个方向思考:
1.双线程DP

可能有人会说直接贪心:先选第1条的最优路径,再选第2条最优路径。
其实我们再选第1条时,我们怎么选会对第2条的路径产生影响,不满足无后效性。
我们选另一种思路:我们可以把问题看作A同时向B传2张纸条,我们令f[i][j][m][n]表示一张纸条在(i,j),另一个在(m,n)时的最优值,这样就满足了无后效性。
易得转移方程:
f[i][j][m][n]=a[i][j]+a[m][n]+max(f[i-1][j][m-1][n],f[i-1][j][m][n-1],f[i][j-1][m-1][n],f[i][j-1][m][n-1]).
同时,我们令f[i][j][i][j]为负无穷即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int m,n,a[60][60],dp[52][52][52][52];
int f(int i,int j,int x,int y){if(dp[i][j][x][y]!=-1){return dp[i][j][x][y];}if(i==x&&j==y) return dp[i][j][x][y]=-10000000;if(i-1>=1&&x-1>=1) dp[i][j][x][y]=max(dp[i][j][x][y],f(i-1,j,x-1,y));if(i-1>=1&&y-1>=1) dp[i][j][x][y]=max(dp[i][j][x][y],f(i-1,j,x,y-1));if(j-1>=1&&x-1>=1) dp[i][j][x][y]=max(dp[i][j][x][y],f(i,j-1,x-1,y));if(j-1>=1&&y-1>=1) dp[i][j][x][y]=max(dp[i][j][x][y],f(i,j-1,x,y-1));dp[i][j][x][y]+=a[i][j]+a[x][y];return dp[i][j][x][y];
}
int main(){cin>>m>>n;memset(dp,-1,sizeof(dp));dp[1][1][1][1]=0;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){cin>>a[i][j];}}cout<<f(m-1,n,m,n-1);
}接题:
2.正难则反+多组DP
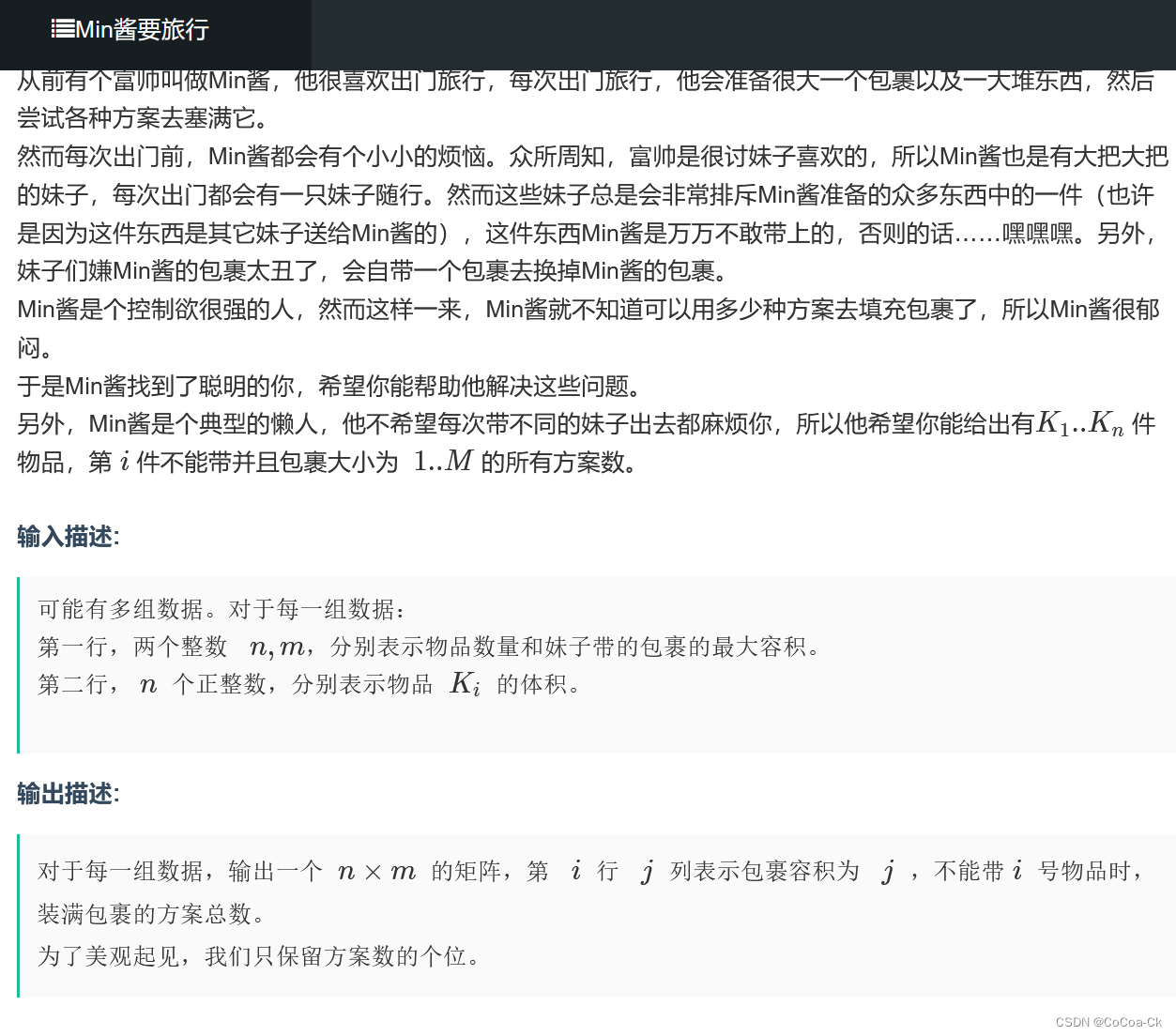
我们自然地想到用g[i][j]表示第i件物品不能带,背包大小为j的方案数。
直接求无从下手,我们考虑他其实就是背包大小为j的方案数-g[i][j-v[i]].
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
#define mod 10
int n,m,f[2350][2350],g[2350][2350],k[2350];
int main(){cin>>n>>m;for(int i=1;i<=n;i++) cin>>k[i];f[0][0]=1;for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){if(j<k[i]) f[i][j]=f[i-1][j]%mod;else{f[i][j]=(f[i-1][j]%mod+f[i-1][j-k[i]]%mod)%mod;}}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(j<k[i]) g[i][j]=f[n][j];else if(j==k[i]) g[i][j]=(f[n][j]-1+mod)%mod;else g[i][j]=(f[n][j]%mod-g[i][j-k[i]]%mod+mod)%mod;cout<<g[i][j]%mod;}cout<<endl;}
}接题:
3.换个方向思考:

如果我们一行一行看,不像互不侵犯可以枚举,于是我们换个角度,我们斜着看,即:

我们发现,在斜着的一列,要敲某一个则必须把他斜上方的都敲了,因此,我们一定是敲的靠上的斜着的某一段。
同时他靠右的一斜列至少要敲到他的层数-1.这样子就合法了。
我们令f[i][j][k]表示前i列共敲了j块,第i列敲了k块。
易得转移方程:
f[i][j][k]=max(f[i-1][j-k][0--(k+1)]+sum[i][k]]).
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,a[60][60],sum[60][60],dp[55][510][55];
int main(){cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=n-i+1;j++){cin>>a[i][j];}}for(int i=1;i<=n;i++){for(int j=1;j<=n-i+1;j++){sum[i][j]=sum[i-1][j]+a[i][j];}}int ans=0;memset(dp,-0x3f,sizeof(dp));dp[n][0][0]=0;dp[n][1][1]=a[1][n];for(int i=n-1;i>=1;i--){for(int j=0;j<=m;j++){for(int k=0;k<=min(n-i+1,j);k++){for(int w=max(k-1,0);w<=n-i;w++){dp[i][j][k]=max(sum[k][i]+dp[i+1][j-k][w],dp[i][j][k]);ans=max(ans,dp[i][j][k]);}}}}cout<<ans;
}