【MATLAB源码-第150期】基于matlab的开普勒优化算法(KOA)机器人栅格路径规划,输出做短路径图和适应度曲线。
操作环境:
MATLAB 2022a
1、算法描述
开普勒优化算法(Kepler Optimization Algorithm, KOA)是一个虚构的、灵感来自天文学的优化算法,它借鉴了开普勒行星运动定律的概念来设计。在这个构想中,算法模仿行星围绕太阳的轨道运动来探索解空间,以寻找最优解。此算法的设计灵感来源于自然界的规律,特别是开普勒定律对行星运动的描述。在详细介绍这个算法之前,先简要回顾一下开普勒的三大定律:
-
第一定律(椭圆轨道定律):每个行星绕太阳旋转的轨道都是椭圆形的,太阳位于椭圆的一个焦点上。
-
第二定律(等面积定律):连接行星和太阳的线段在相同时间内覆盖的面积相等。
-
第三定律(调和定律):行星绕太阳公转的周期的平方与其轨道半长轴的立方成正比。
基于上述定律,开普勒优化算法构建了一个模拟的太阳系,其中待优化问题的潜在解被视为行星,而当前最优解则是太阳。接下来,我们将详细探讨算法的主要组成部分、运作机制以及其在实际问题中的应用。
算法组成
初始化:在解空间内随机生成一组解,这些解代表行星,每个行星具有其位置和速度。同时,从这些解中选择一个当前最优解作为太阳。
迭代过程:
-
行星运动:每个行星根据其速度和与太阳的相对位置进行移动。行星的运动轨迹旨在模仿开普勒定律描述的天体运动,尤其是等面积定律,确保搜索过程既广泛又深入。
-
速度和位置更新:行星的速度和位置根据其与太阳的相对关系动态更新,以模拟行星绕太阳旋转的物理行为。
-
评估和更新太阳位置:在每次迭代中,所有行星的适应度(即解的质量)被评估,最优的行星可能成为新的太阳,即当前最优解。
终止条件:算法运行直到满足预定的停止条件,如达到最大迭代次数或解的质量不再显著改善。
算法特点
全局搜索能力:通过模拟行星的广泛运动,KOA具有在整个解空间内进行搜索的能力,有助于避免局部最优解。
自适应调整机制:行星的运动轨迹和速度根据与太阳的相对位置动态调整,使得算法能够根据当前搜索情况自适应地调整探索策略。
平衡探索与开发:等面积定律的应用有助于算法在新的搜索区域(探索)和已知的优秀区域(开发)之间保持平衡。
应用领域
开普勒优化算法由于其独特的搜索机制,适用于多种优化问题,包括但不限于:
-
工程设计优化:在工程设计中寻找最优参数配置。
-
机器学习和深度学习:自动调整模型参数以提高性能。
-
经济学模型:寻找最优的经济决策和资源分配方案。
-
物流优化:优化货物配送路线,减少成本和时间。
结论
开普勒优化算法将天文学原理与优化理论结合起来,提供了一种新颖的全局优化方法。通过模拟行星围绕太阳的运动,它能够有效地探索解空间,寻找到问题的最优解。虽然这里描述的KOA是一个理论上的构想,但它展示了自然现象与算法设计之间的交叉创新潜力,为解决复杂优化问题提供了新的思路和灵感。在未来,这种算法有可能被进一步研究和开发,以应对实际世界中的各种挑战。
2、仿真结果演示

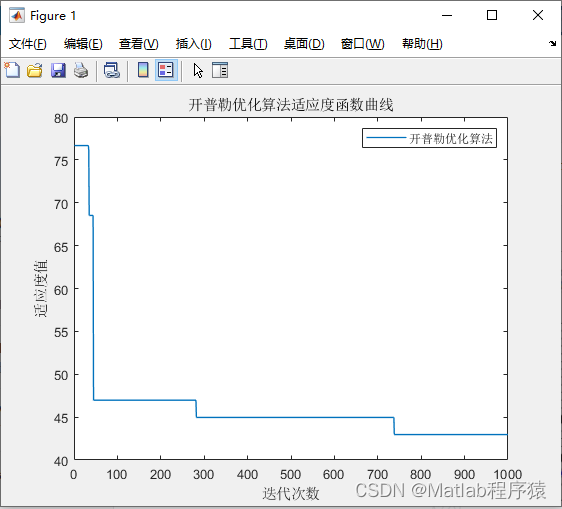
3、关键代码展示
略
4、MATLAB 源码获取
V
点击下方名片
