备战蓝桥杯---树形DP基础3
上一次我们讲了二叉苹果树,现在我们加一点难度,从二叉变成了多叉苹果树。
这样子我们就不可以直接按照上次的方法DP,我们其实可以发现,我们可以用类似背包的思想求解,这就是所谓的树上背包。
我们先加进第一个儿子来跟新1--m的解,然后再让第二个进来更新,这样子就求出来了。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,q,x,y,head[200],v[200],cnt,z,dp[110][110];
struct node{int dian,next,quan;
}edge[210];
void merge(int x,int y,int z){edge[++cnt].dian=y;edge[cnt].quan=z;edge[cnt].next=head[x];head[x]=cnt;
}
void dfsquan(int root,int fa){for(int i=head[root];i!=-1;i=edge[i].next){if(edge[i].dian==fa) continue;v[edge[i].dian]=edge[i].quan;dfsquan(edge[i].dian,root);}return;
}
void dfsdp(int root,int fa){for(int j=q+1;j>=1;j--){dp[root][j]=v[root];}dp[root][0]=0;for(int i=head[root];i!=-1;i=edge[i].next){if(fa==edge[i].dian) continue;int ckck=edge[i].dian;dfsdp(ckck,root);for(int j=q+1;j>=1;j--){for(int k=0;k<=j-1;k++){dp[root][j]=max(dp[ckck][k]+dp[root][j-k],dp[root][j]);}}}
}
int main(){cin>>n>>q;memset(head,-1,sizeof(head));for(int i=1;i<=n-1;i++){cin>>x>>y>>z;merge(x,y,z);merge(y,x,z);}dfsquan(1,-1);dfsdp(1,-1);cout<<dp[1][q+1];
}这里有两点注意:
1.v[root]操作不应该放在循环里面,否则会重复操作(若为边权可以)
2.转移方程中应为dp[root][j-k]而不是dp[root][j-k-1],因为root时已经把root点算进去了,不用为root留空间。
接题:

其实我们可以不用DP:
我们可以先选任意一点DFS求出权值最大的子链,我们可以证明权值最大的子链的端点之一一定是这个DFS后的端点。
下面进行证明:
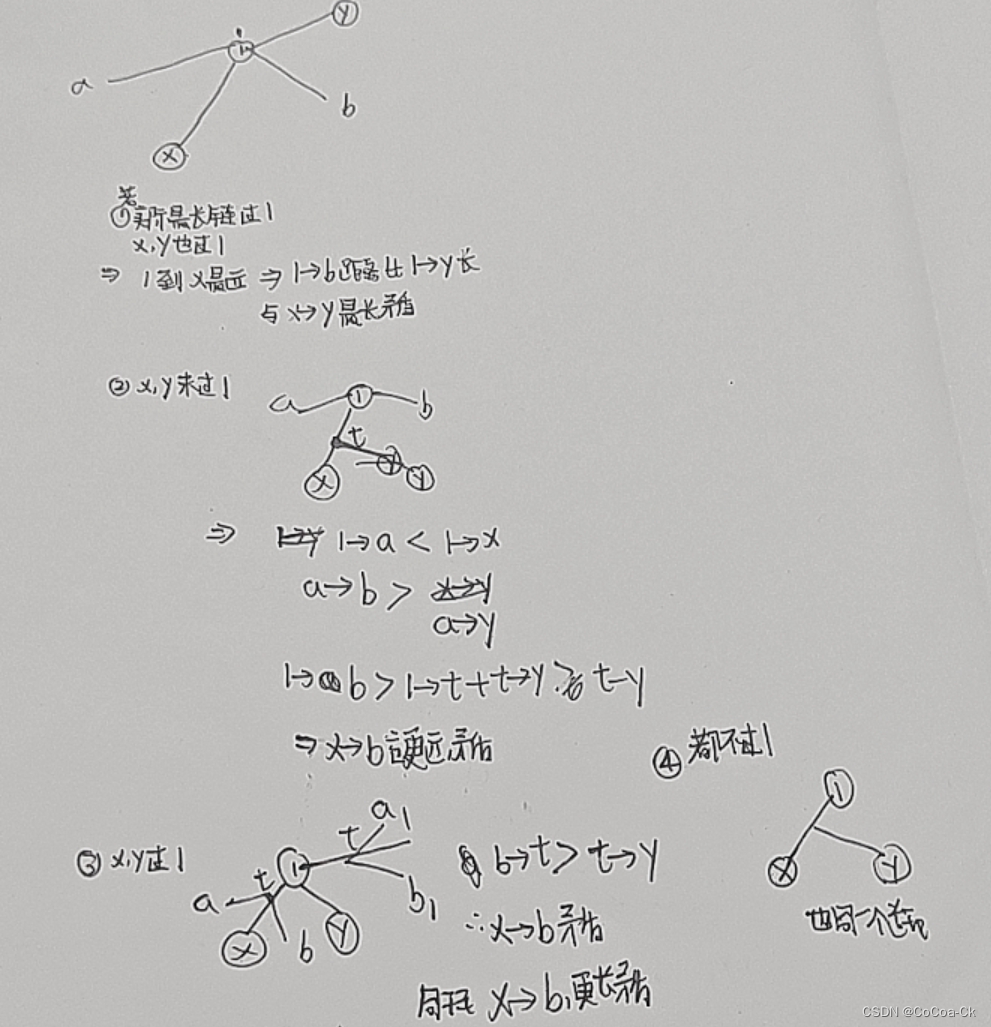
我们再来看看树形DP的解法:
我们令f[i]表示以i为根的子树的最大子链,有两种情况,1.它经过i 2.他没有经过
对于经过i,我们只要把以i为起点DFS的最大长度与第二大长度相加即可。
这里我们可以简化一下:
我们令ans为答案值,dp[i]为以i为起点的最大权值,我们在求dp[i]的同时维护ans即可。
其中相加操作dp[i]记录了到目前为止的最大值(有点类似背包),通过dp[i]+dp[v]就实现了最大值与次大值相加的操作,最后维护一下dp[i]即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
struct node1{int dian,next;
}edge[200010];
int head[100010],n,a[100010],cnt,u,v,dp[100010],ans=-10000000;
void merge(int x,int y){edge[++cnt].dian=y;edge[cnt].next=head[x];head[x]=cnt;
}
void dfsdp(int root,int fa){dp[root]=a[root];ans=max(ans,a[root]);for(int i=head[root];i!=-1;i=edge[i].next){if(edge[i].dian==fa) continue;dfsdp(edge[i].dian,root);ans=max(ans,dp[edge[i].dian]);ans=max(ans,dp[root]+dp[edge[i].dian]);dp[root]=max(dp[root],a[root]+dp[edge[i].dian]);}return;
}
signed main(){cin>>n;memset(head,-1,sizeof(head));for(int i=1;i<=n;i++){scanf("%lld",&a[i]);}for(int i=1;i<=n-1;i++){scanf("%lld%lld",&u,&v);merge(u,v);merge(v,u);}dfsdp(1,-1);cout<<ans;
}