当前位置：首页 > news >正文

数据结构与算法之堆排序

news 2025/7/28 21:21:47

堆排序概述

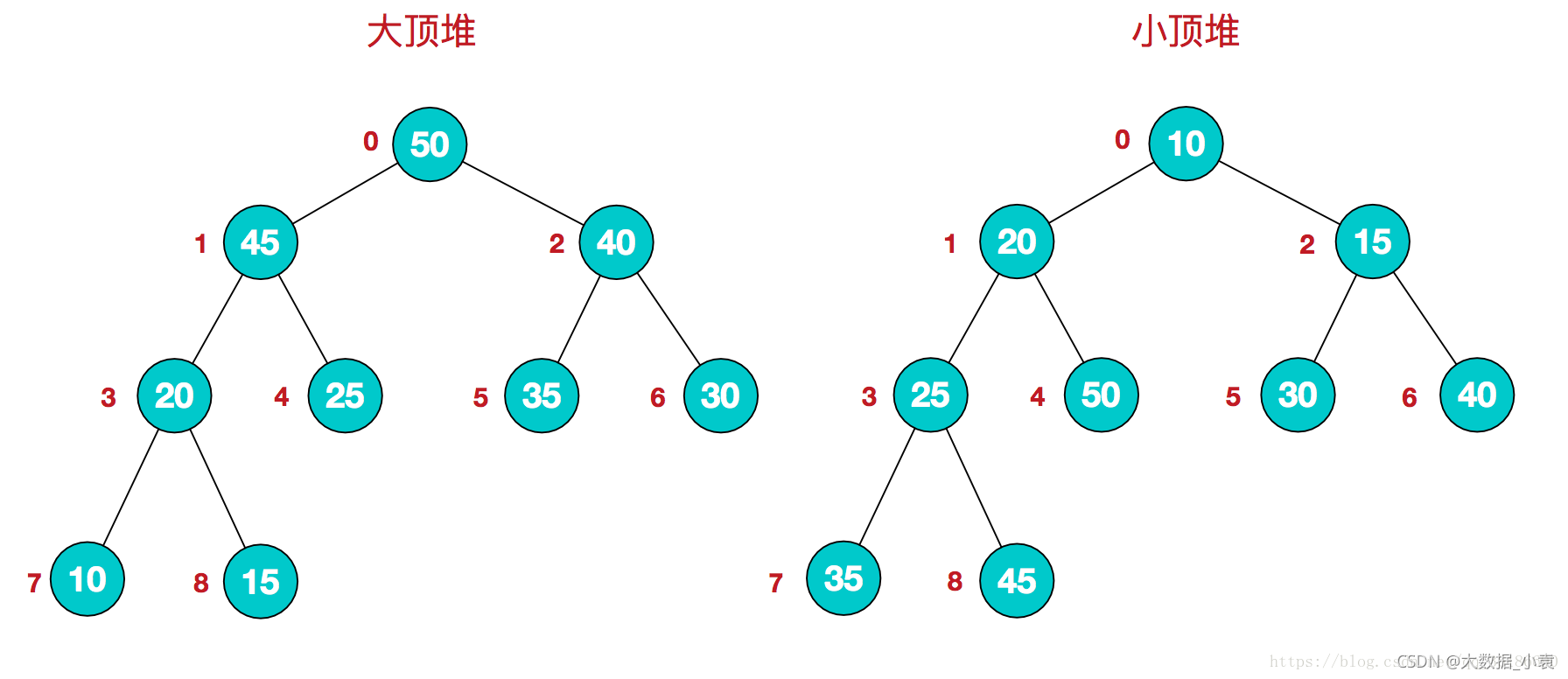
堆排序（Heap Sort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。如下图：

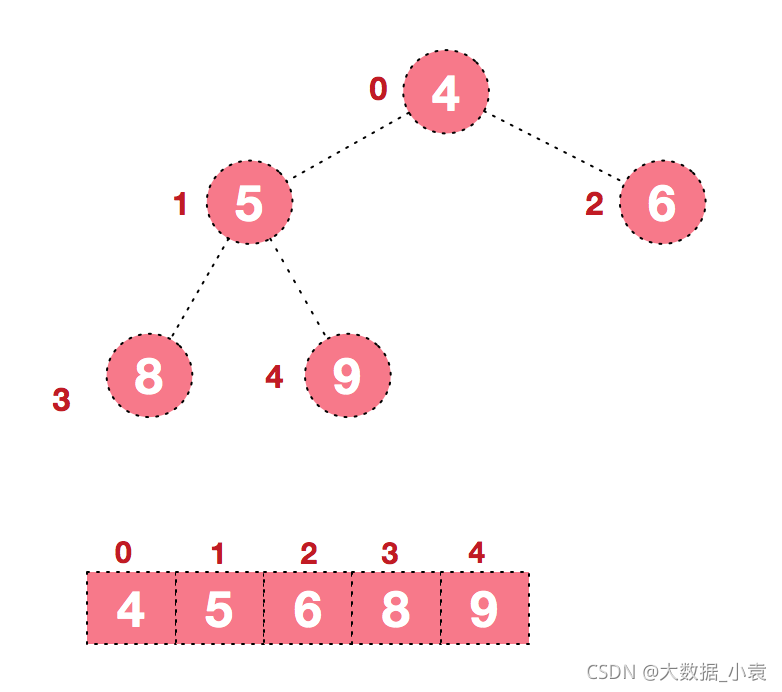
在这里插入图片描述同时，我们对堆中的结点按层进行编号，将这种逻辑结构映射到数组中就是下面这个样子
该数组从逻辑上讲就是一个堆结构，我们用简单的公式来描述一下堆的定义就是：

大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

步骤一构造初始堆。将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)

1）假设给定无序序列结构如下
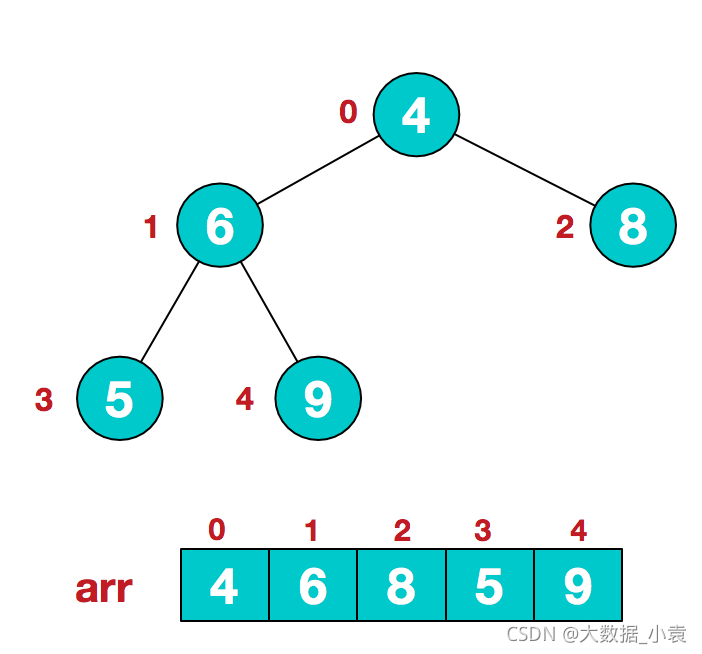
在这里插入图片描述
2）此时我们从最后一个非叶子结点开始（叶结点自然不用调整，第一个非叶子结点 arr.length/2-1=5/2-1=1，也就是下面的6结点），从左至右，从下至上进行调整

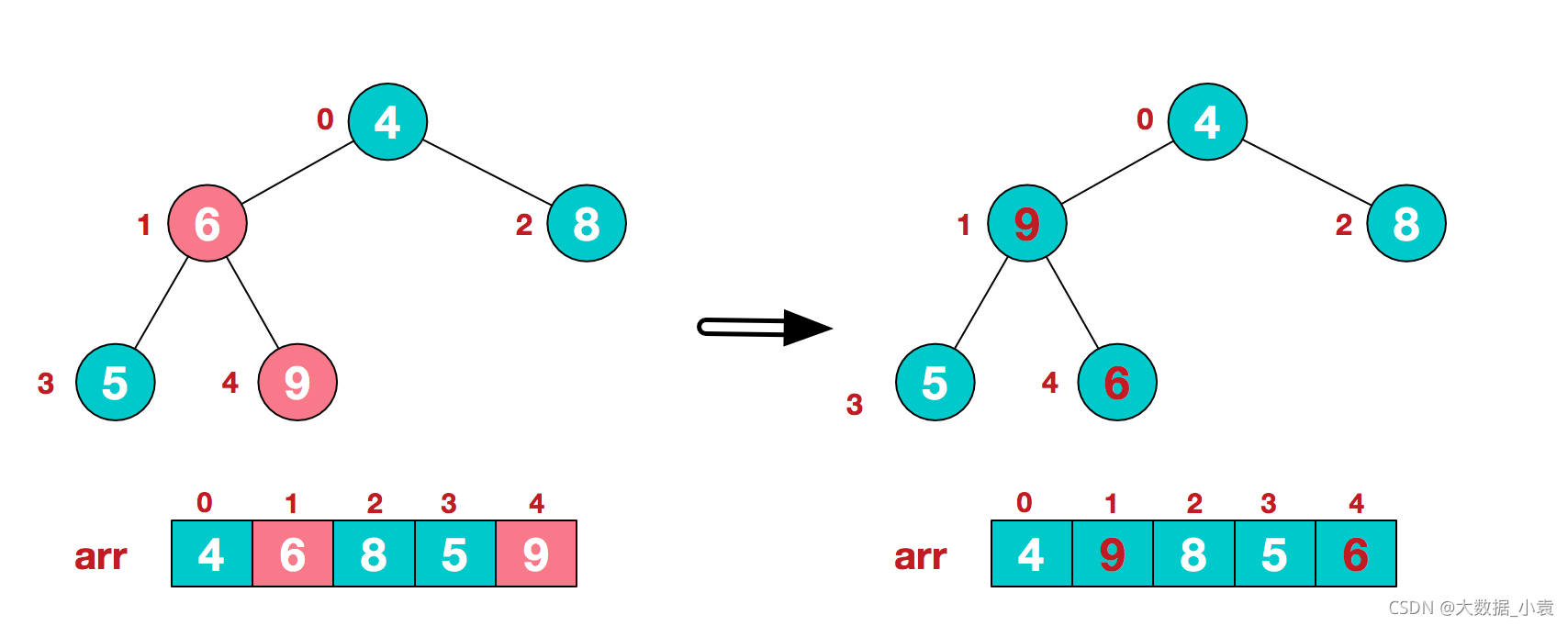
3）找到第二个非叶节点4，由于[4,9,8]中9元素最大，4和9交换
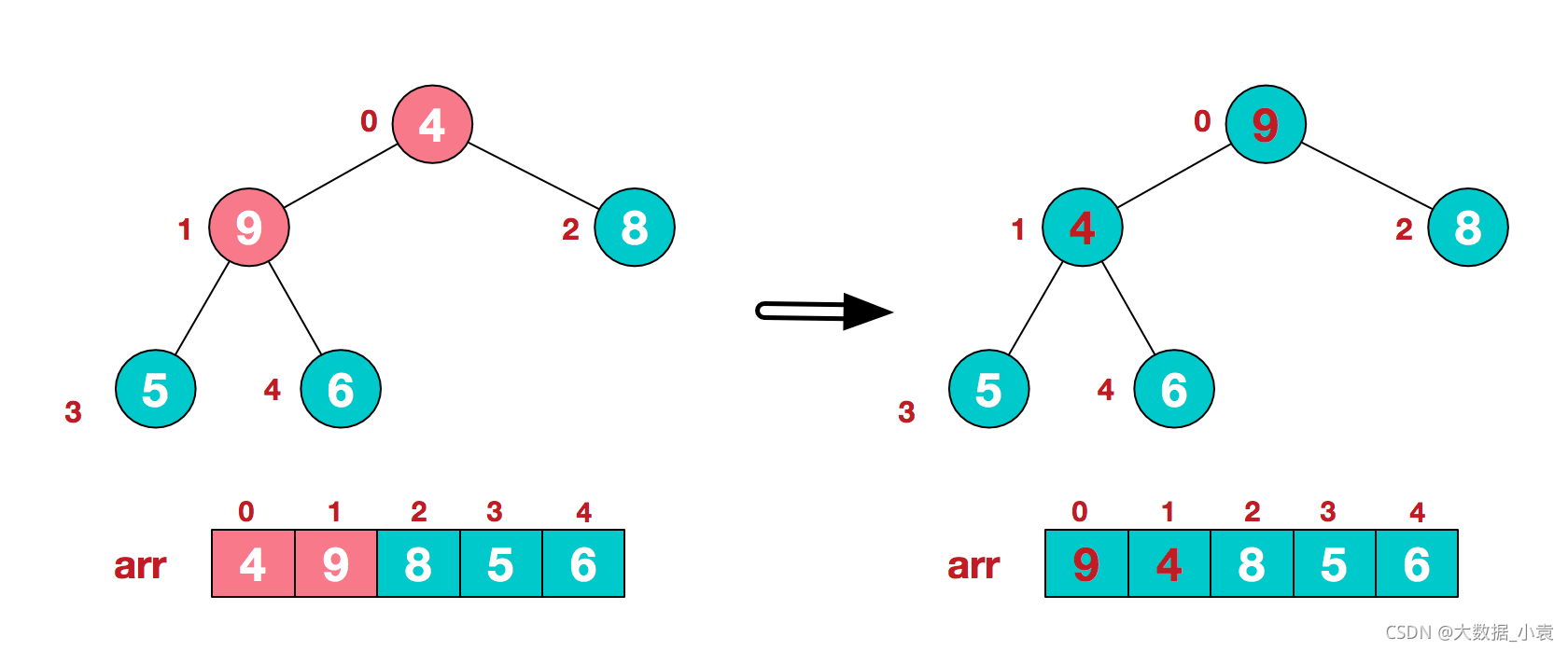在这里插入图片描述 4）这时，交换导致了子根[4,5,6]结构混乱，继续调整，[4,5,6]中6最大，交换4和6。
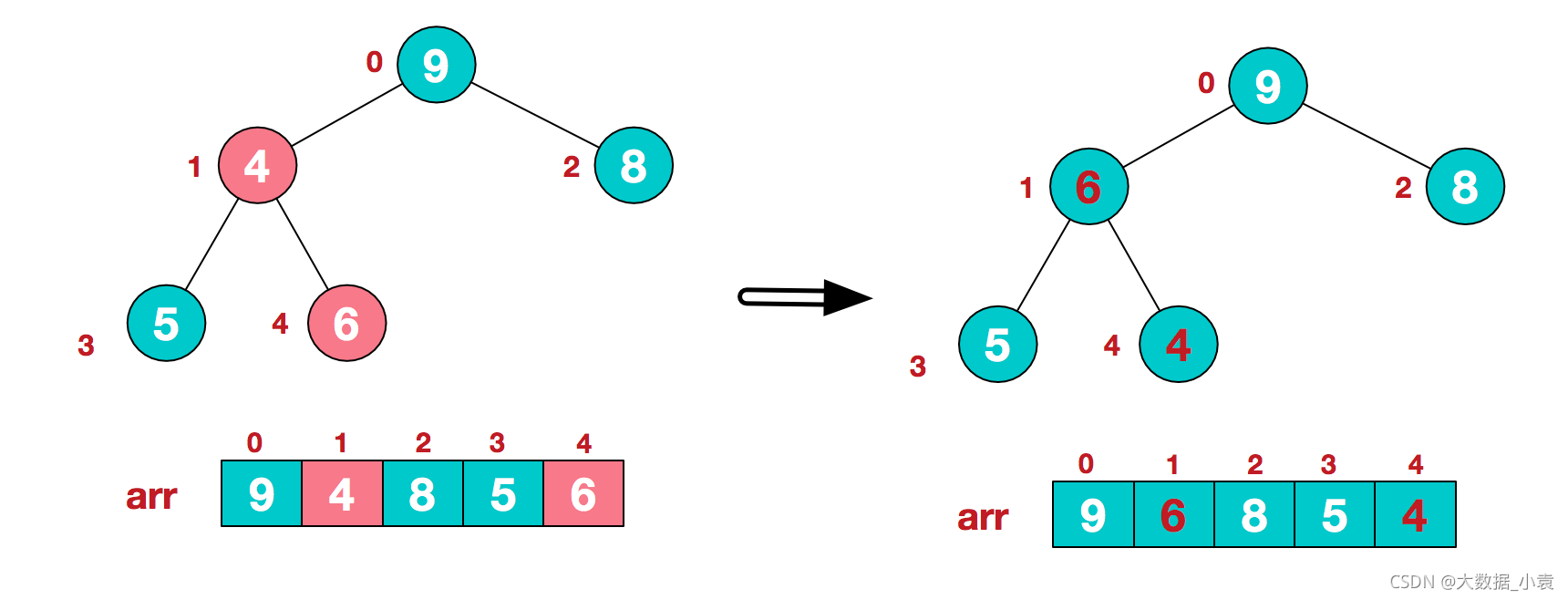此时，我们就将一个无需序列构造成了一个大顶堆

步骤二将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换

1）将堆顶元素9和末尾元素4进行交换，9就不用继续排序了
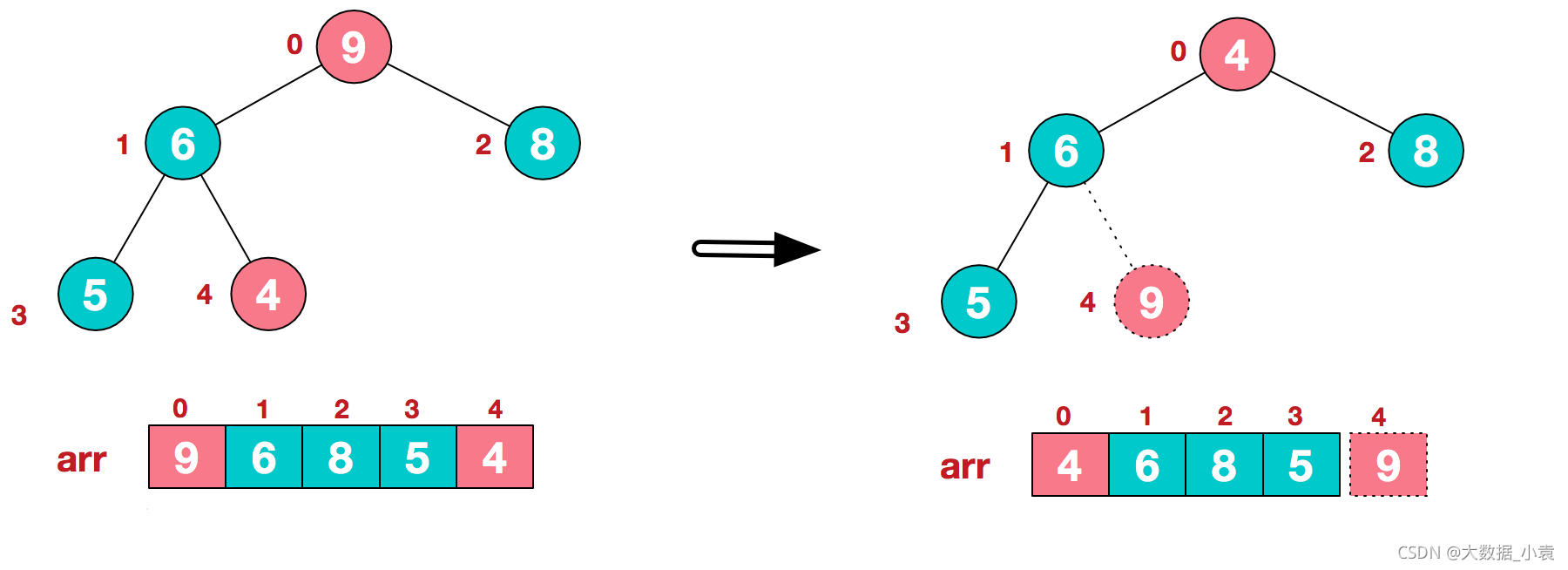
在这里插入图片描述
2）重新调整结构，使其继续构建大顶堆（9除外）

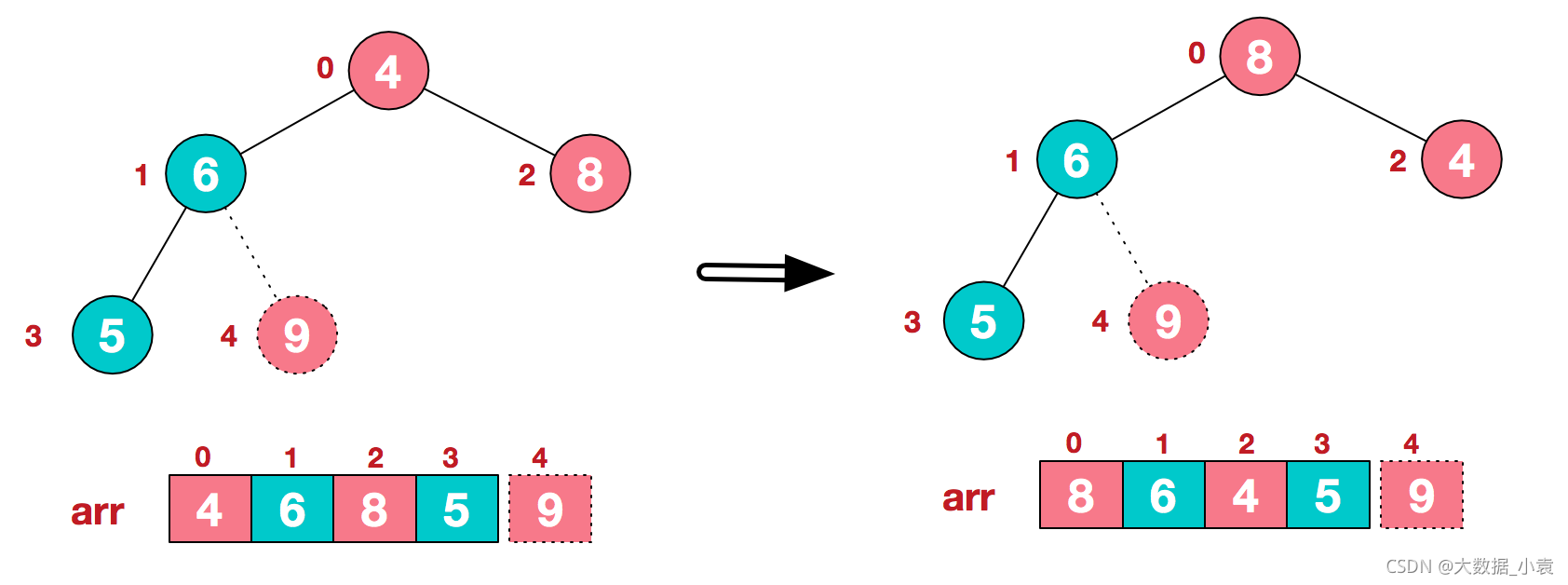
3）再将堆顶元素8与末尾元素5进行交换，得到第二大元素8.

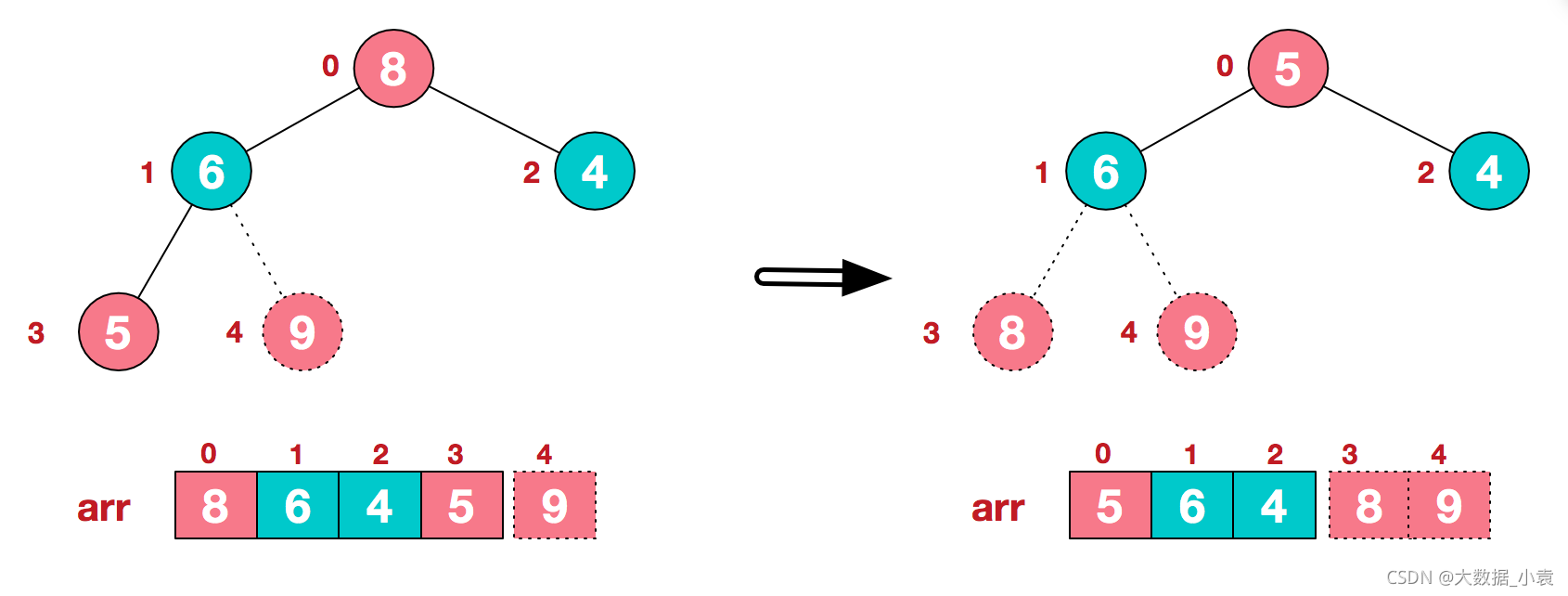
步骤三后续过程，继续进行调整，交换，如此反复进行，最终使得整个序列有序

排序思路：

将无需序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;
将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;
重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序

动图展示：

在这里插入图片描述

代码实现

import java.util.Arrays;public class HeapSort {public static void main(String[] args) {int[] arr = {4, 6, 8, 5, 9};heapSort(arr);
//        [4, 6, 8, 5, 9]
//        [4, 9, 8, 5, 6]
//        [4, 9, 8, 5, 6]
//        [9, 6, 8, 5, 4]
//        [9, 6, 8, 5, 4]
//        [9, 6, 8, 5, 4]
//        [8, 6, 4, 5, 9]
//        [8, 6, 4, 5, 9]
//        [6, 5, 4, 8, 9]
//        [6, 5, 4, 8, 9]
//        [5, 4, 6, 8, 9]
//        [5, 4, 6, 8, 9]
//        [4, 5, 6, 8, 9]}//堆排序public static void heapSort(int[] arr) {//开始位置是最后一个非叶子节点（最后一个节点的父节点）int start = (arr.length - 1) / 2;//循环调整为大顶堆for (int i = start; i >= 0; i--) {maxHeap(arr, arr.length, i);}//先把数组中第0个和堆中最后一个交换位置for (int i = arr.length - 1; i > 0; i--) {int temp = arr[0];arr[0] = arr[i];arr[i] = temp;//再把前面的处理为大顶堆maxHeap(arr, i, 0);}}//数组转大顶堆,size:调整多少（从最后一个向前减），index:调整哪一个（最后一个非叶子节点）public static void maxHeap(int[] arr, int size, int index) {//左子节点int leftNode = 2 * index + 1;//右子节点int rightNode = 2 * index + 2;//先设当前为最大节点int max = index;//和两个子节点分别对比，找出最大的节点if (leftNode < size && arr[leftNode] > arr[max]) {max = leftNode;}if (rightNode < size && arr[rightNode] > arr[max]) {max = rightNode;}//交换位置if (max != index) {int temp = arr[index];arr[index] = arr[max];arr[max] = temp;//交换位置后，可能会破坏之前排好的堆，所以之间排好的堆需要重新调整maxHeap(arr, size, max);}//打印每次排序后的结果System.out.println(Arrays.toString(arr));}
}