备战蓝桥杯---动态规划之经典背包问题
看题:
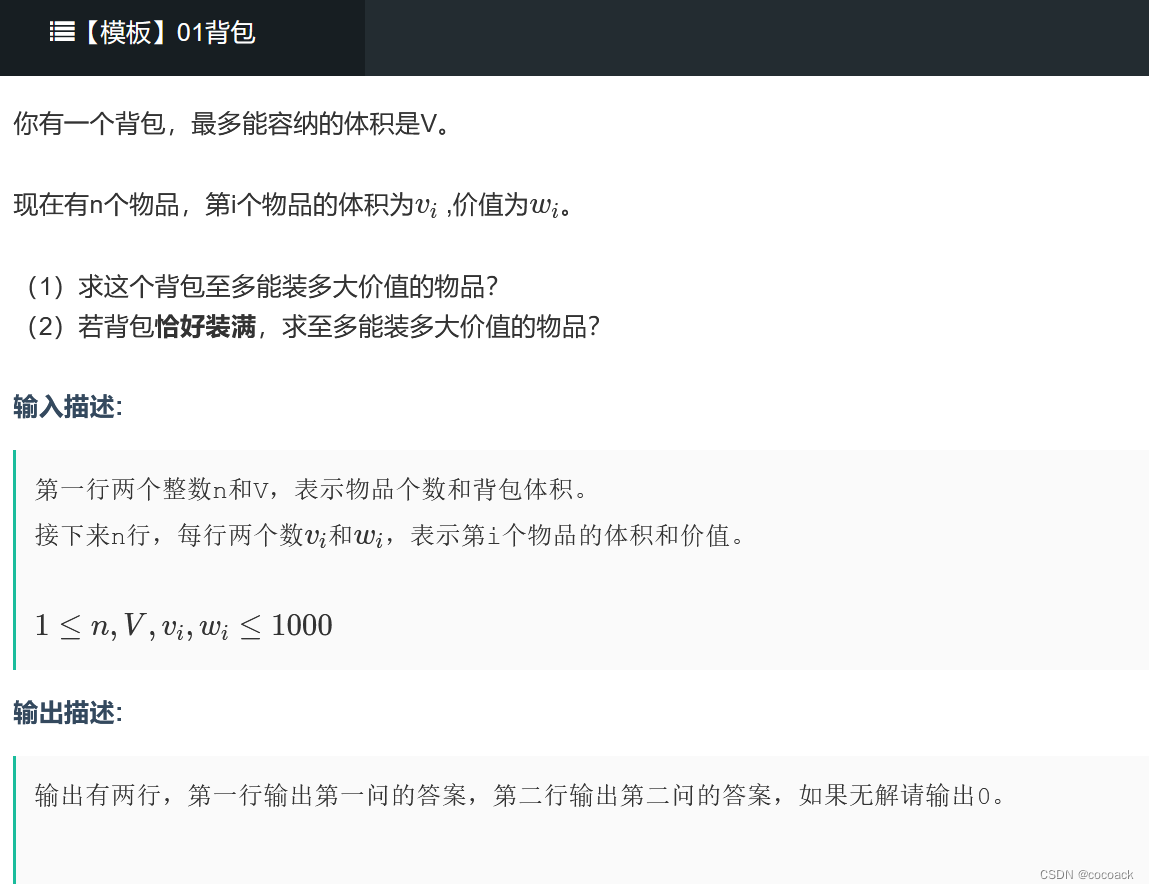
我们令f[i][j]为前i个物品放满容量为j的背包的最大价值。
f[i][j]=max(f[i-1][j],f[i-1][j-c[i]]+w[i]);
我们开始全副成负无穷。f[0][0]=0;最后循环最后一行求max;
负无穷:0xc0c0c0c0;正无穷:0x3f3f3f3f
下面是v=12,n=6的图示:

下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,v1,v[1002],w[1002],dp[1002][1002];
signed main(){cin>>n>>v1;for(int i=1;i<=n;i++) scanf("%d%d",&v[i],&w[i]);memset(dp,-0x3f,sizeof(dp));dp[0][0]=0;for(int i=1;i<=n;i++){for(int j=0;j<=v1;j++){if(j>=v[i]) dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i]);else dp[i][j]=dp[i-1][j];}}int ans=0;for(int i=0;i<=v1;i++){ans=max(ans,dp[n][i]);}cout<<ans<<endl;if(dp[n][v1]<=0) cout<<0;else cout<<dp[n][v1];
}事实上,我们可以想象一些有体积但是没有价值的空气,显然,他不会影响最后的结果,而且它保证了对于每一行它的值递增,因此我们for循环可以省去。(不过这个前提是题目保证不一定要塞满)
加点难度:
n<=20,v<=10^9;N小,我们直接DFS
n<=100,v<=10^9:
我们可以用map来存每一行的值,对于负无穷,我们直接忽略,对于那先体积比小的大但是价值比他们小的也舍弃。
下面是代码:
#include<bits/stdc++.h>
using namespace std;
int n,v[1005],v1,w[1005],q;
map<int,int> ck[2];
int main(){cin>>n>>v1;for(int i=1;i<=n;i++) scanf("%d%d",&v[i],&w[i]);ck[0][0]=0;map<int,int>::iterator it;map<int,int>::iterator it1;for(int i=1;i<=n;i++){it=ck[(i-1)%2].begin();it1=ck[(i-1)%2].begin();while((it1->first)<v[i]&&it1!=ck[(i-1)%2].end()){ck[i%2][it1->first]=it1->second;it1++;}q=(--it1)->second;while(it!=ck[(i-1)%2].end()){if(it->first+v[i]>v1) break;if(ck[(i-1)%2].count(it->first+v[i])!=0){ck[i%2][it->first+v[i]]=max(ck[(i-1)%2][it->first]+w[i],ck[(i-1)%2][it->first+v[i]]);}else ck[i%2][it->first+v[i]]=ck[(i-1)%2][it->first]+w[i];if(q<ck[i%2][it->first+v[i]]) q=ck[i%2][it->first+v[i]];else{ck[i%2].erase(it->first+v[i]);}it++;}ck[(i-1)%2].clear();}cout<<(--ck[n%2].end())->second<<endl;
}接下来我们看一下完全背包:

很容易,我们可得:f[i][j]=max(f[i-1][j-k*c[i]]+k*w[i])(0<=k*c[i]<=j)
其中,复杂度为k*n*v;
f[i][j]=max(f[i-1][j],f[i-1][j-c]+w,f[i-1][j-2*c]+2*w,.........)
f[i][j-c]=max(f[i-1][j-c],f[i-1][j-2*c]+w,......)
于是,f[i][j]=max(f[i][j-c]+w,f[i-1][j])
这样,我们就把复杂度->n*v;
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,v1,v[1005],w[1005],dp[1005];
int main(){cin>>n>>v1;memset(dp,0xc0c0c0c0,sizeof(dp));for(int i=1;i<=n;i++) scanf("%d%d",&v[i],&w[i]);dp[0]=0;for(int i=1;i<=n;i++){for(int j=v[i];j<=v1;j++){dp[j]=max(dp[j],dp[j-v[i]]+w[i]);}}int ans=0;for(int i=0;i<=v1;i++) ans=max(ans,dp[i]);cout<<ans<<endl;if(dp[v1]<0) cout<<0;else cout<<dp[v1];
}看看多重背包:
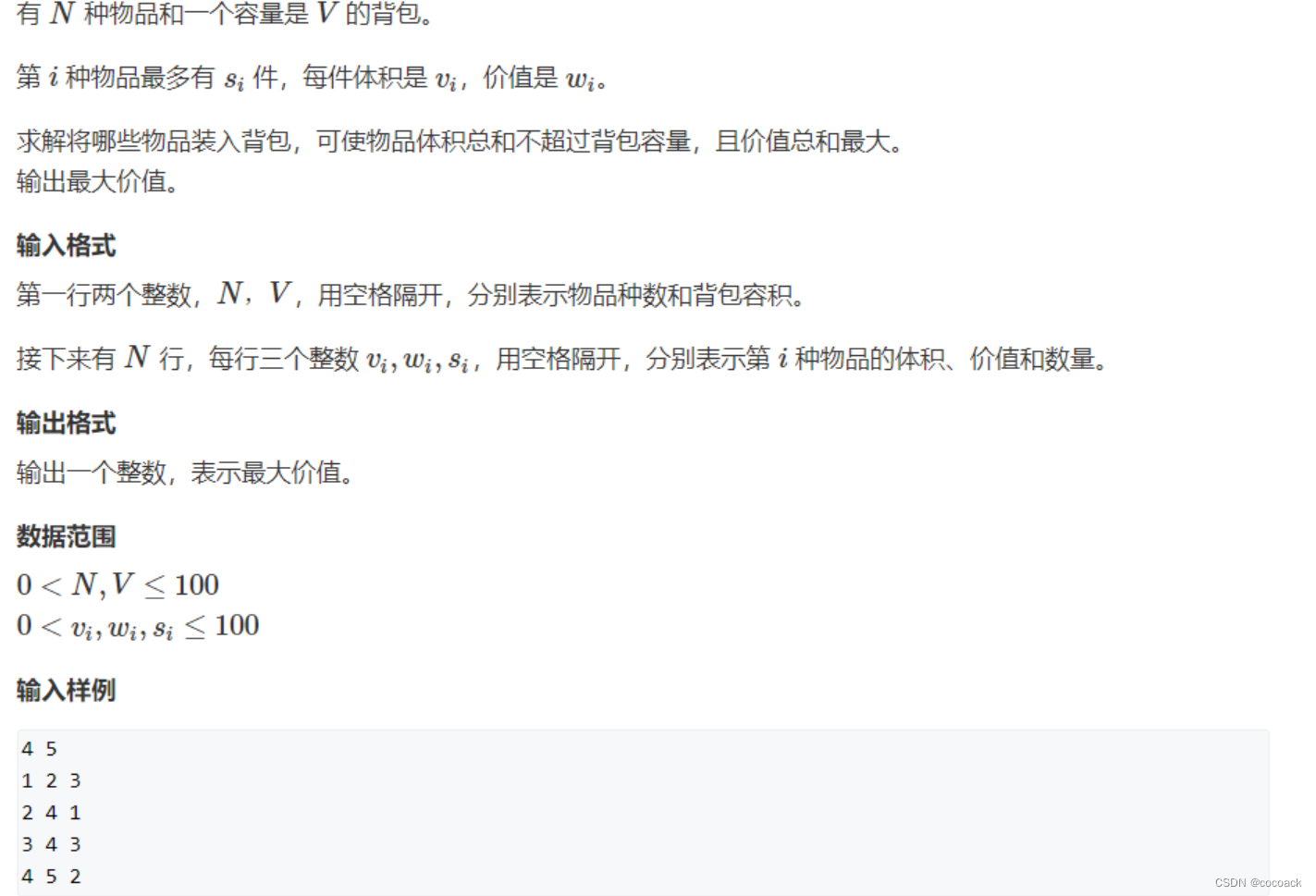
我们可以吧一样的背包看成不一样的,这样就转化为求0/1背包,但是这样的复杂度还是和上一题类似。
我们考虑优化一下:
假如有7个物品,我们如何用跟小的数字表示它所有的方案?
我们可以采用二进制的思想--》1,2,4包,每一个方案可以组合成所有可能。
我们把数分成1,2,4,8....加上剩余的数即可。
下面是二进制压缩代码:
for(int i=1;i<=n;i++){int a,b,c;scanf("%d%d%d",&a,&b,&c);int k=1;while(k<c){v[cnt]=k*a;w[cnt++]=k*b;c-=k;k*=2;}if(c){v[cnt]=c*a;w[cnt]=c*b;}}