当前位置：首页 > news >正文

C++ 搜索二叉树的删除

news 2025/7/28 21:37:12

首先查找元素是否在二叉搜索树中，如果不存在，则返回

要删除的结点可能分下面四种情况：

a. 要删除的结点无孩子结点

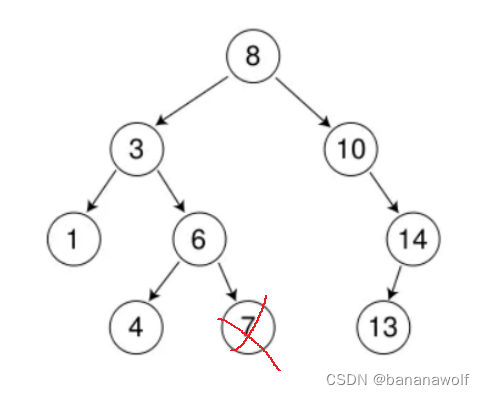
b. 要删除的结点只有左孩子结点

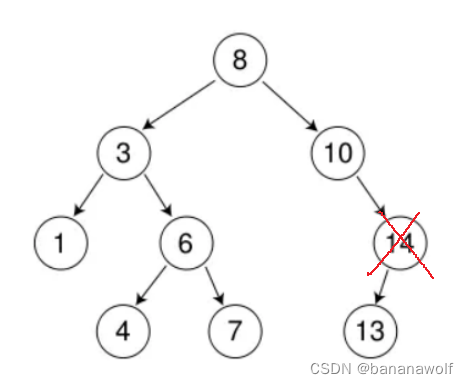
c. 要删除的结点只有右孩子结点

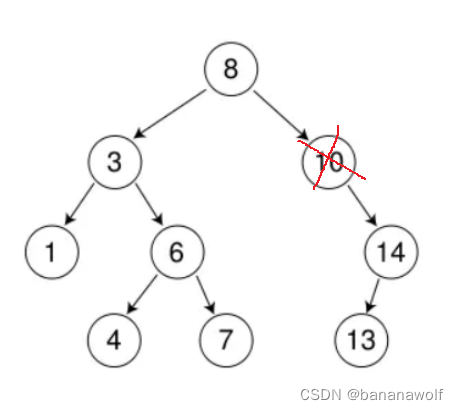
d. 要删除的结点有左、右孩子结点

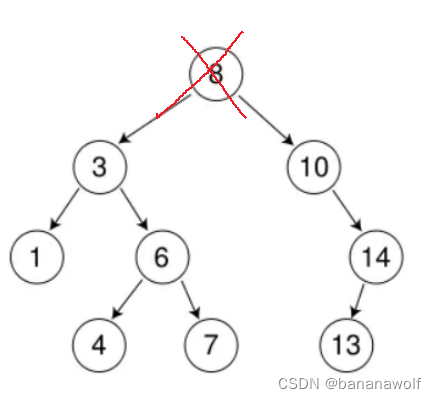
看起来有待删除节点有4中情况，实际情况a可以与情况b或者c合并起来，因此真正的删除过程如下：

情况1：删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点--直接删除

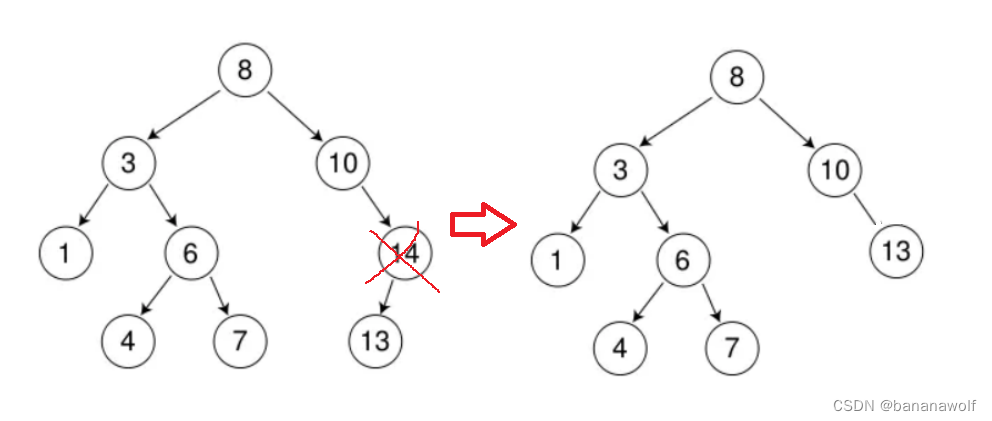
情况2：删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点--直接删除

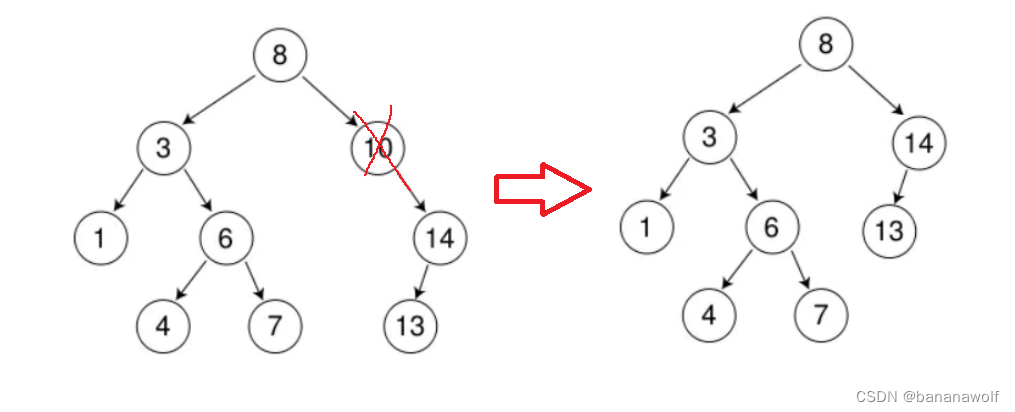
情况3：找它的右子树的最小值或者左子树的最大值，用它的值填补到被删除节点中，再来处理该结点的删除问题--替换法删除

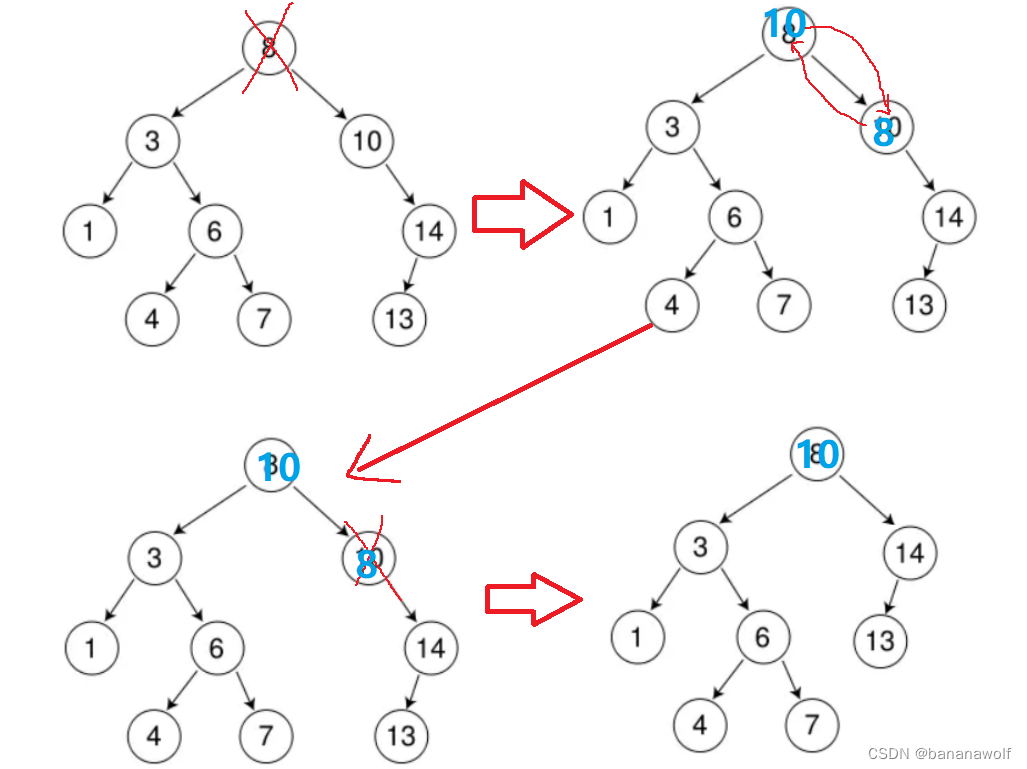
tip：

我们可以把一个父节点看作父亲，每一个父亲只能照顾两个儿子

情况1和情况2：如果这个父亲只有一个孩子要照顾，或者一个也没有，那么他想要脱身，只需要把这个孩子托付给他的长辈，没有就是nullptr，我们可以把这个过程叫托孤

情况3：就比较复杂，这个父亲有两个孩子，托孤就行不通了，所以他要找一个人来代替他，他需要满足两个条件：

首先，要确保他是可以脱身的（他要是有一个孩子就托孤），这样他就可以过来照顾这两个孩子了

其次，他要满足照顾这两个孩子的条件，这个节点的key值要比左子树的每个节点key都要大，比右子树的每个节点key都要小，

右子树的最小值或者左子树的最大值就满足这些条件，我们可以把这个过程叫找月嫂

bool Erase(const K& data)
{node* parent = nullptr;node* cur = _root;while (cur && cur->_data != data)//找要删除的位置{parent = cur;if (data < cur->_data){cur = cur->_left;}else{cur = cur->_right;}}if (cur == nullptr)return false;if (cur->_left == nullptr)//托孤给父母{if (parent == nullptr)//考虑特殊root==nullptr{_root = cur->_right;}else{if (cur->_data < parent->_data)parent->_left = cur->_right;elseparent->_right = cur->_right;}delete cur;}else if (cur->_right == nullptr)//托孤给父母{if (parent == nullptr)//考虑特殊root==nullptr{_root = cur->_left;}else{if (cur->_data < parent->_data)parent->_left = cur->_left;elseparent->_right = cur->_left;}delete cur;}else//找月嫂替代（合适 有且只有一个娃或者没有）{node* maxleft = cur->_left;node* maxparent = cur;while (maxleft->_right){maxparent = maxleft;maxleft = maxleft->_right;}cur->_data = maxleft->_data;// maxparent->_right = maxleft->_left;错误//月嫂托孤if (maxparent->_left == maxleft)//maxparent==cur{maxparent->_left = maxleft->_left;}else{maxparent->_right = maxleft->_left;}delete maxleft;}return true;
}

注意特殊情况：

1.在情况一和情况二下，可能删除_root节点，在函数里面就需要特殊考虑

2.情况三，月嫂的托孤，月嫂不一定是父亲的右孩子（左子树最大值的前提下），月嫂可能就是要被删除节点的左孩子，所以也要妥善处理

递归版

bool _EraseR(node*& root, const K& data)
{if (root == nullptr)return false;if (data < root->_data)return _EraseR(root->_left, data);else if (data > root->_data)return _EraseR(root->_right, data);else{node* del = root;if (root->_left == nullptr){root = root->_right;delete del;}else if (root->_right == nullptr){root = root->_left;delete del;}else{node* maxleft = root->_left;while (maxleft->_right)maxleft = maxleft->_right;del = maxleft;swap(root->_data, maxleft->_data);_EraseR(root->_left, data);//转为子问题}return true;}
}