Dijkstra算法(求最短路)
简介:
迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959年提出的,因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法,解决的是有权图中最短路径问题。
特点:
迪杰斯特拉算法采用的是一种贪心策略,其主要特点是从起始点开始,每次遍历到始点距离最近且未访问过的顶点的邻接节点,直到扩展到终点为止。
时间复杂度:O(n*n)
使用场景:从一个顶点到其余各顶点的最短路径(权重不可为负)
Dijkstra算法思路
初始步骤:记录初始节点到其余各点的距离(初始为真无穷大),并在循环步骤中不断更新
核心循环步骤:
- 每次从未标记的节点中选择距离出发点最近的节点,标记,收录到最优路径集合中
- 计算刚加入节点A的临近节点B的距离(不含标记的节点),若(节点A的距离+节点A到节点B的边长)< 节点B的距离,就更新节点B的距离和前面点
代码模版:

例:计算节点A到所有节点的最短路径
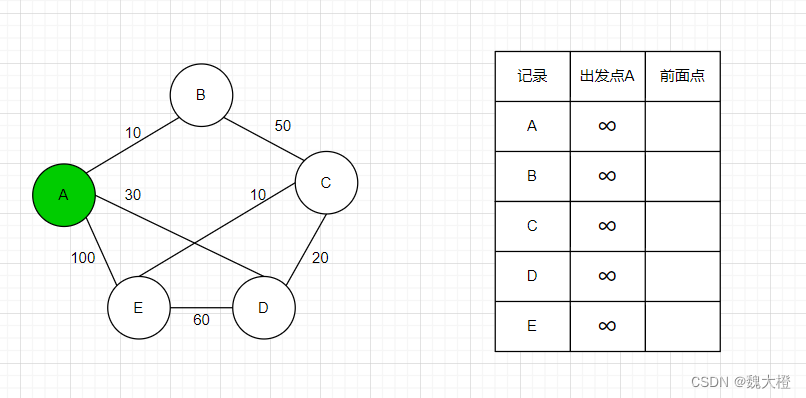
步骤一:节点A计算到节点A的距离
因为是自己到自己所以距离为0,更新表格

然后在未标记的节点中寻找距离出发点最小的节点,为节点A并收录进最优路径节点中
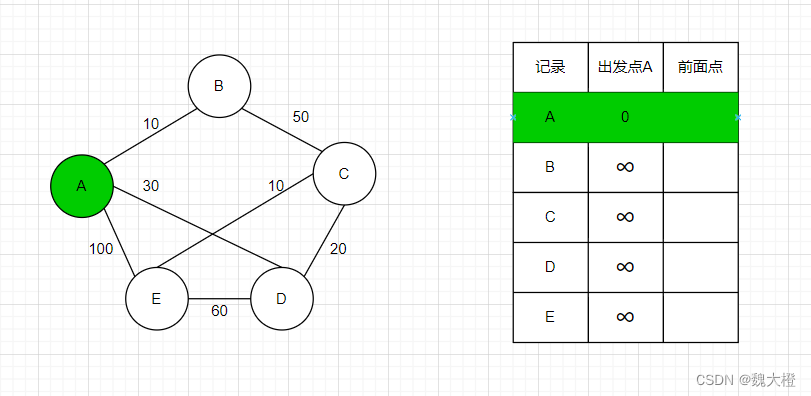
步骤二:更新节点A临近的节点B、D、E的距离
由A到节点B、D、E的距离为10、30、100,因为比无穷大要小,所以更新表格中B、D和E的距离
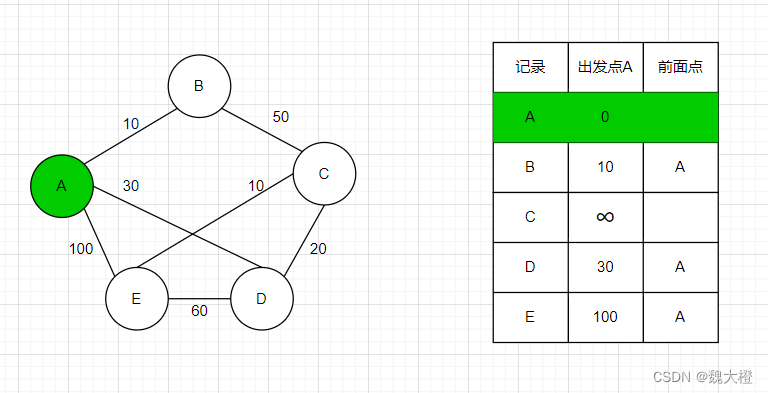
然后在未标记的节点中寻找距离出发点最小的节点,为节点B并收录进最优路径节点中
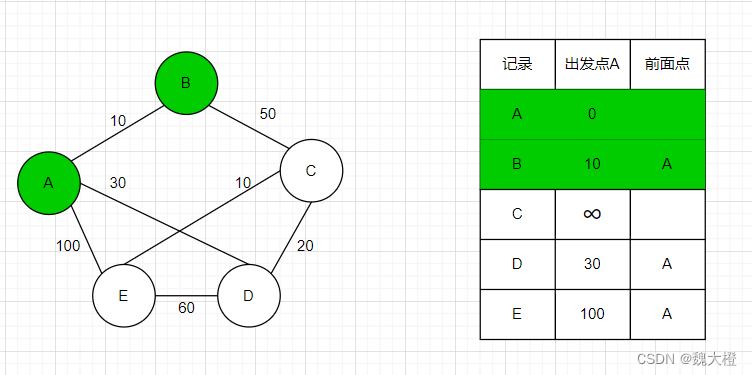
步骤三:尝试更新节点B的临近节点C
节点B到节点C的距离为50,那么节点A到节点C就有一条经过节点B的路径,距离为60,小于无穷大,更新表格
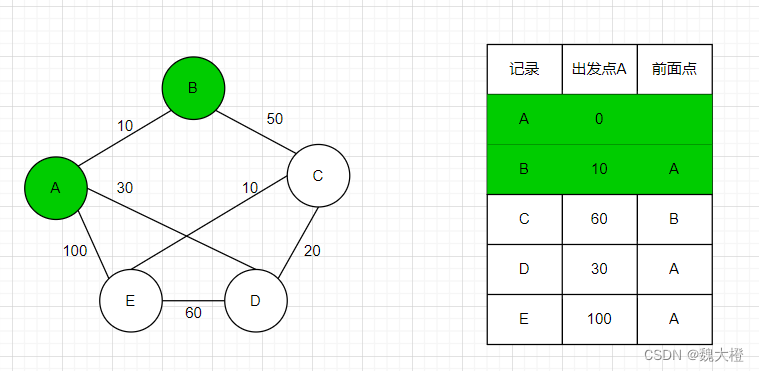
然后在未标记的节点中寻找距离出发点最小的节点,为节点D并收录进最优路径节点中
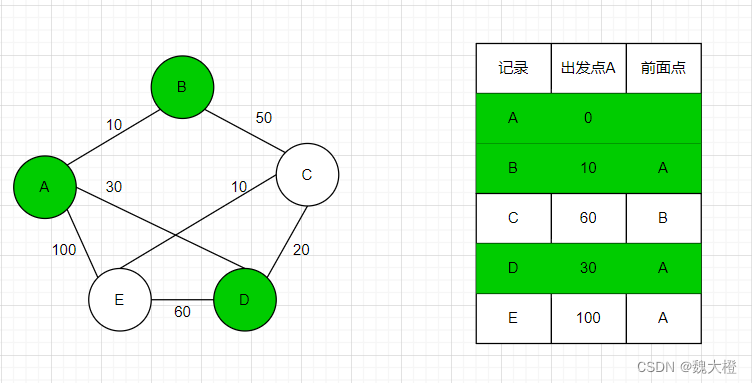
步骤四:更新节点D的临近节点C和E的距离
节点D到节点C的距离为20,那么节点A经过节点D到节点C的路径距离为50,小于60,即距离小于原本经过B到C的路径距离,更新表格
节点D到节点E的距离为60。那么从A经过节点D到E的距离为90,小于100,更新表格。
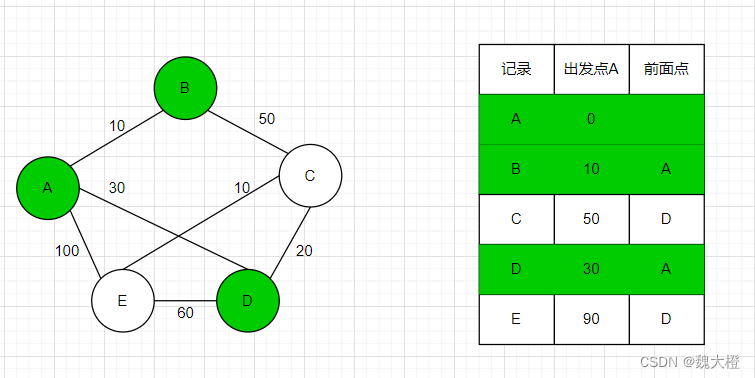
然后在未标记的节点中寻找距离出发点最小的节点,为节点C并收录进最优路径节点中
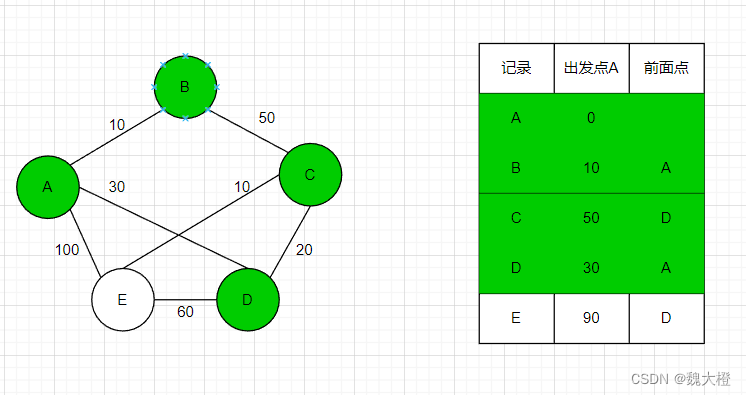
步骤五:更新节点C的临近节点E
节点C到节点E的距离为10,那么从A经过节点D、C到达的节点E距离为60,小于90,更新表格
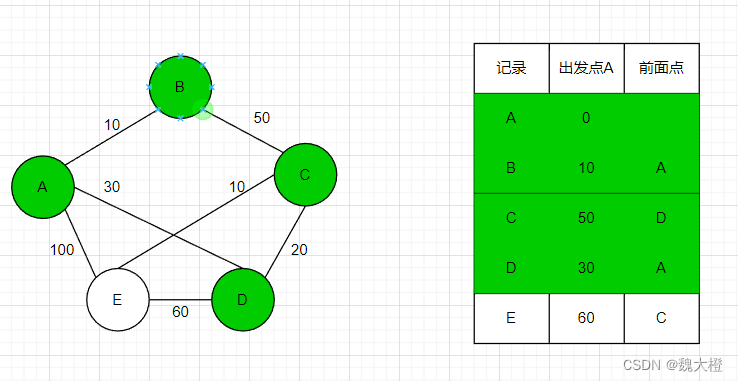
然后在未标记的节点中寻找距离出发点最小的节点,为节点E并收录进最优路径节点中
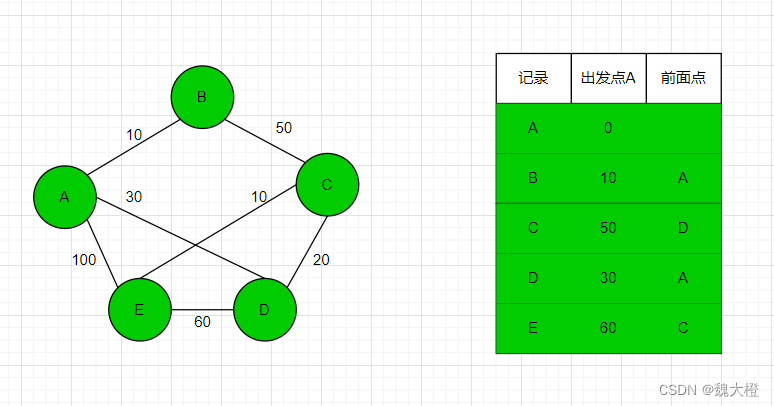
至此,所以节点皆被标记,因此所有节点的最短路径也在表格中写出
