当前位置：首页 > news >正文

计算机图形学实验

news 2025/8/20 11:42:11

题目要求

1.1 实验一：图元的生成：直线、圆椭区域填充
你需要完成基本的图元生成算法，包括直线和椭圆。
在区域填充中，要求你对一个封闭图形进行填充。你需要绘制一个封
闭图形（例如多边形），并选择一种算法进行区域填充。
你的作品应当有一定的交互功能，例如，通过鼠标确定控制点来获得
以上图形。
1.2 实验二：样条曲线的生成： Bezier Bezier 曲线、B-样条
曲线的生成：
你需要完成这两种曲线的生成。
对于桂栭样条曲线，统一要求实现均匀二次桂栭样条曲线。
你的作品应当有一定的交互功能，例如，通过鼠标左键确定控制点，
双击绘制曲线。
1.3 实验三：分形图的生成： Koch 曲线、Mandelbrot Mandelbrot
集和Julia 集、蕨类植物（自选两个）
以上有栴个实验内容，自选栲个做实验即可。
对于实验中涉及的参数，不做统一要求。
1.4 实验四：真实感图形的生成：显示一个具有场景，几何造型
自定义包括消隐、镜面反射纹理效果
场景自选，几何体造型自选。可以是正方体、球体等简单图形，鼓励
使用复杂一点的真实感图形。

实验效果

总体框架

使用Python编程语言，利用PyQt5库进行代码实现，只使用PyQt5的画点函数实现所有图元生成。

PyQt5是基于Qt库的Python GUI开发框架，提供了丰富的图形用户界面组件和功能，支持跨平台应用程序的开发。通过连接信号与槽，开发者可以实现事件驱动的应用程序，并可使用Qt Designer工具进行可视化界面设计。PyQt5具备多线程支持、数据库连接功能，是一个开源、跨平台的强大工具，使得开发者能够轻松创建各种桌面应用程序。

整体的软件实现分为三个部分：CG_UI、Main、Algorithm。其中CG_UI是通过PyQt5设计的实验UI界面程序，Algorithm是各种图元生成算法的实现，Main实现的是与使用者的交互，以及对图元生成算法的调用和在UI界面的绘制。整体的设计逻辑为，使用者在UI界面进行相应的坐标点选择、参数选择、算法选择过程，Main将使用者的需求处理为具体的指令，调用相应的生成算法，计算出需要在UI界面绘制的坐标点的集合，再进行最终坐标点的绘制，即完成了图元生成过程。

主程序涉及的人机交互事件主要包括按键交互事件、鼠标点击事件以及绘制事件，为了统一化的设计，我将所有试验都合并设计为了一个软件，软件界面如下图所示。
在这里插入图片描述

同时，我们也设计了良好的交互提示逻辑，防止软件出现bug。例如，当你在画直线时，只在画图界面中绘制了一个坐标点就点击“生成直线”时，就会弹出下图警告，而不执行相应的命令，防止出现bug。

# 在这里插入图片描述

实验一图元生成

直线生成算法

圆和椭圆生成
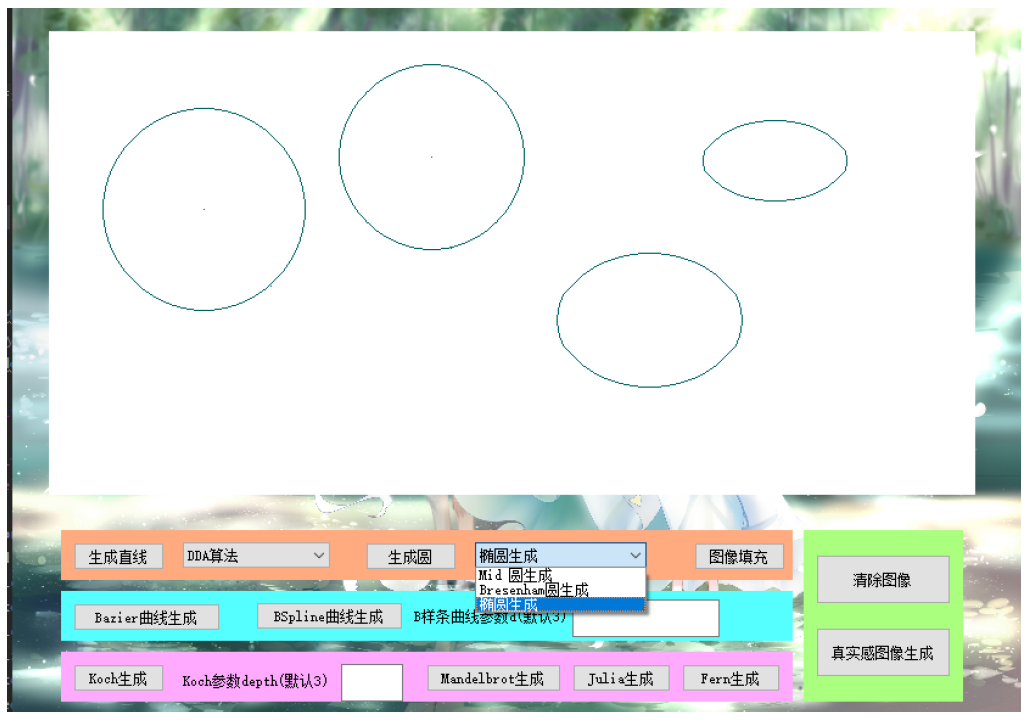
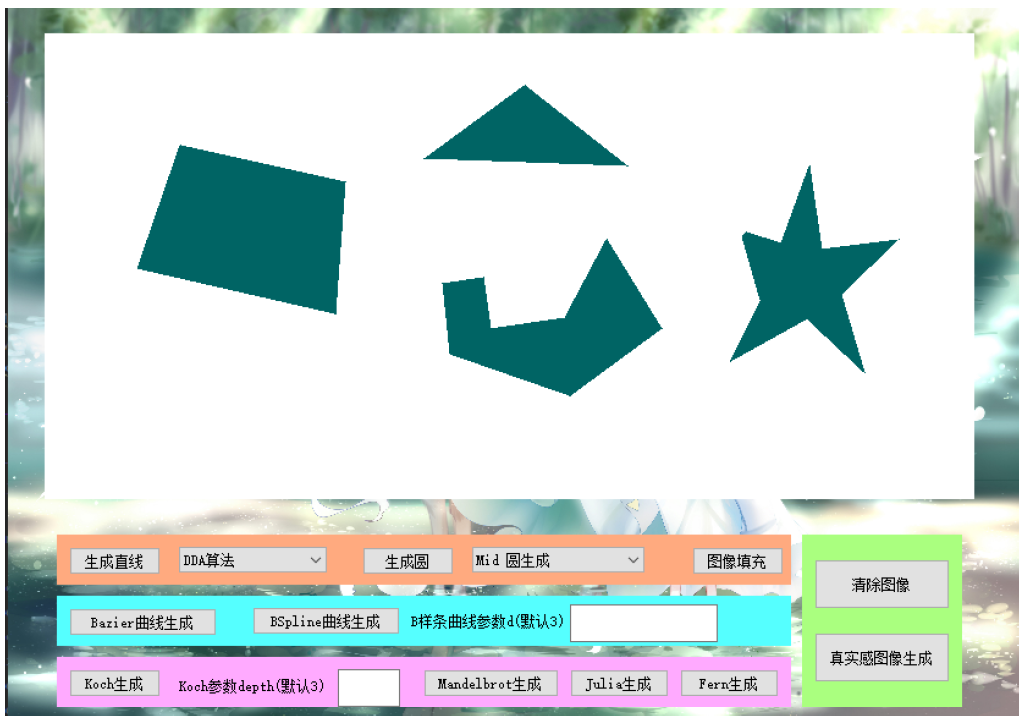
在这里插入图片描述

图像填充

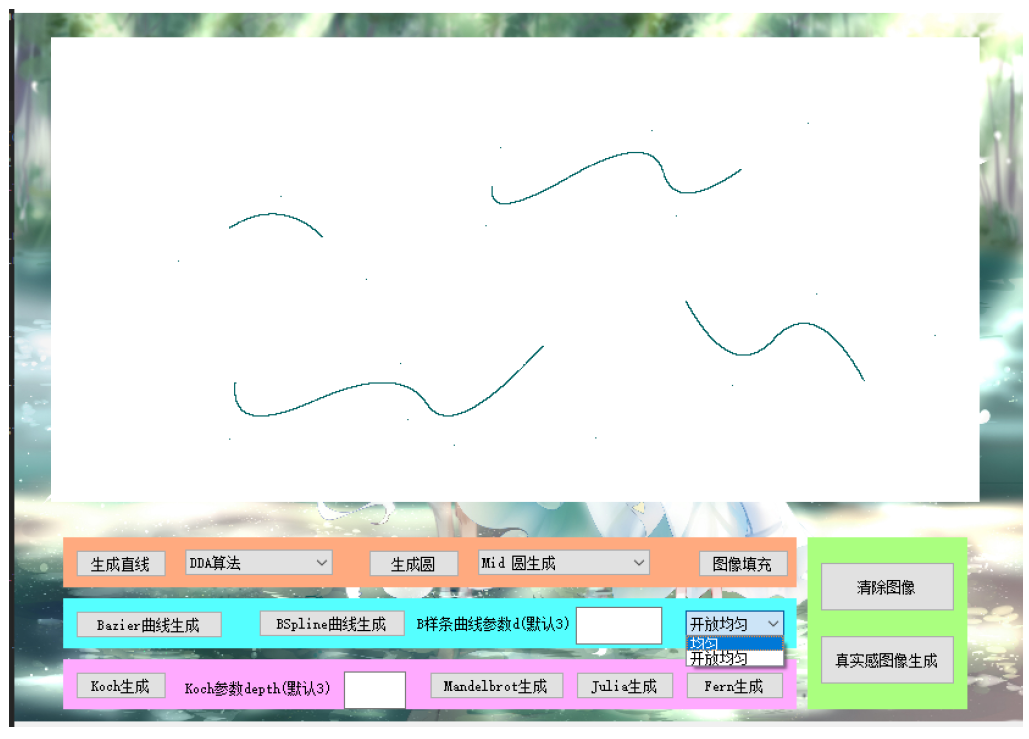
在这里插入图片描述

实验二曲线

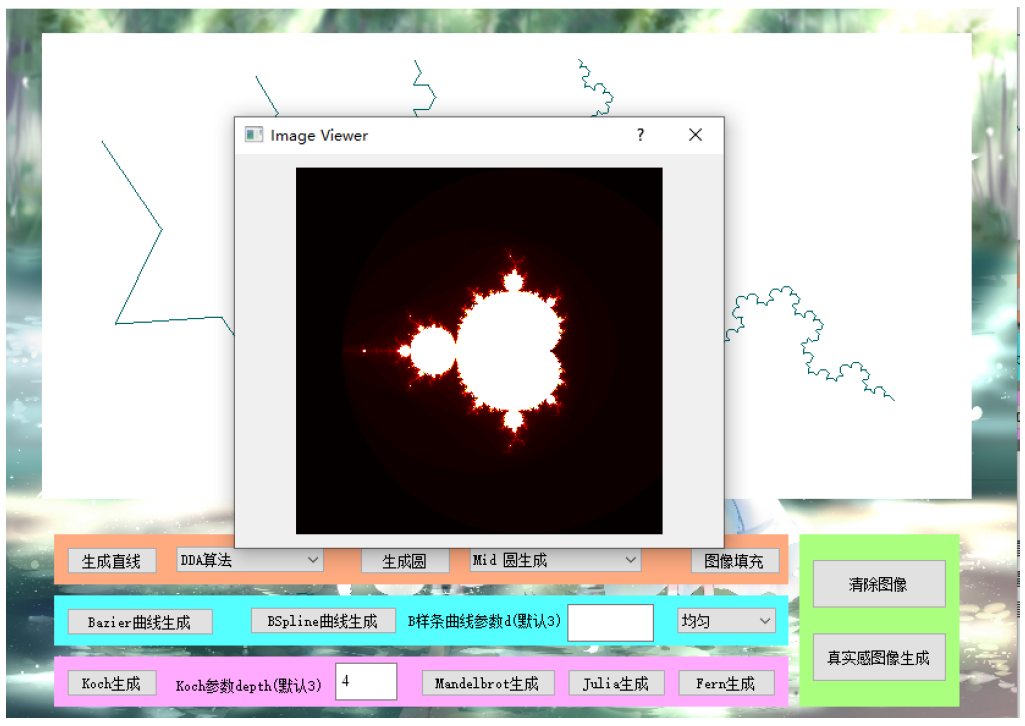
在这里插入图片描述

实验三分形图生成

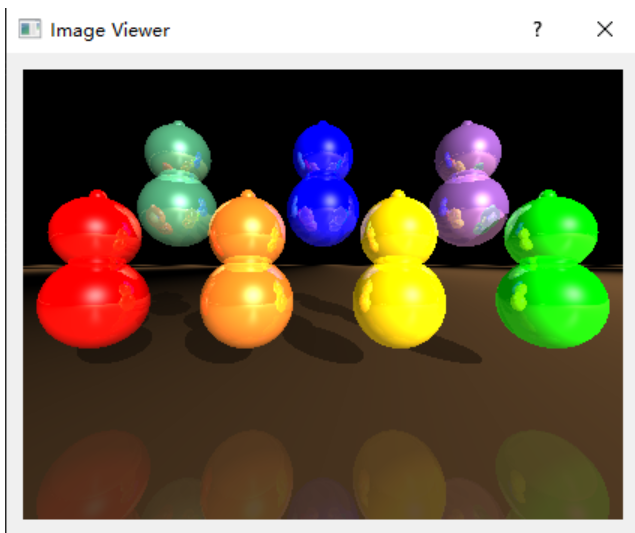
在这里插入图片描述

实验四真实感图形生成

在这里插入图片描述

代码

完整代码和软件+Q:1695251905或CSDN私信
部分代码：

class Line():def __init__(self):passdef swapPoint(self,point):""" swap start-point with end-point  """temp = point[0]point[0] = point[1]point[1] = tempdef DDA(self, point, graph_points):"""DDA algorithm generate line"""dx = float(point[1][0] - point[0][0])dy = float(point[1][1] - point[0][1])m = dy / (dx+1e-9)if abs(m) <= 1:"""if abs(slope) less than 1, x_k+1 = x_k + 1, y_k+1 = y_k + m"""if point[0][0] > point[1][0]:self.swapPoint(point)k = dy / dxx = point[0][0]y = float(point[0][1])for x in range(point[0][0], point[1][0]):graph_points.append((x, int(y)))y += kelse:"""if abs(slope) more than 1, y_k+1 = y_k + 1, x_k+1 = x_k + 1/m"""if point[0][1] > point[1][1]:self.swapPoint(point)k = dx / dy  # 斜率的倒数y = point[0][1]x = float(point[0][0])for y in range(point[0][1], point[1][1]):graph_points.append((int(x), y))x += kdef MidPoint(self, point, graph_points):"""MID algorithm generate line"""dx = point[1][0] - point[0][0]dy = point[1][1] - point[0][1]m = dy / dxif m > 1:"""slop > 1"""if point[0][1] > point[1][1]:self.swapPoint(point)# a = y2 - y1, b = x1 - x2b = point[1][0] - point[0][0]a = point[0][1] - point[1][1]# 判别参数p0 = a + 2 * b（扩大两倍）p = a + 2 * bd1 = 2 * (a + b)d2 = 2 * b# 初始点x = point[0][0]y = point[0][1]graph_points.append((x,  y))while y < point[1][1]:"""y_k+1 = y_k + 1"""y += 1if p < 0:"""if p < 0, 中点在线下, x_k+1 = x_k, p_k+1 = p_k + d2"""p += d2else:"""if p > 0, 中点在线上, x_k+1 = x_k + 1, p_k+1 = p_k + d1"""p += d1x += 1graph_points.append((x,  y))elif m >= 0 and m <= 1:"""斜率大于0小于1"""if point[0][0] > point[1][0]:self.swapPoint(point)# a = y2 - y1, b = x1 - x2b = point[1][0] - point[0][0]a = point[0][1] - point[1][1]# 判别参数p0 = 2 * a + b（扩大两倍）p = 2 * a + bd1 = 2 * (a + b)d2 = 2 * a# 初始点x = point[0][0]y = point[0][1]graph_points.append((x,  y))while x < point[1][0]:"""x_k+1 = x_k + 1"""x += 1if p < 0:"""if p < 0, 中点在线下, y_k+1 = y_k + 1, p_k+1 = p_k + d1"""p += d1y += 1else:"""if p > 0, 中点在线上, y_k+1 = y_k, p_k+1 = p_k + d2"""p += d2graph_points.append((x,  y))elif m < 0 and m >= -1:"""斜率小于0大于-1"""if point[0][0] > point[1][0]:self.swapPoint(point)# a = y2 - y1, b = x1 - x2b = point[1][0] - point[0][0]a = point[0][1] - point[1][1]# 判别参数p0 = 2 * a - b（扩大两倍）p = 2 * a - bd1 = 2 * (a - b)d2 = 2 * a# 初始点x = point[0][0]y = point[0][1]graph_points.append((x,  y))while x < point[1][0]:"""x_k+1 = x_k + 1"""x += 1if p < 0:"""if p < 0, 中点在线下, y_k+1 = y_k, p_k+1 = p_k + d2"""p += d2else:"""if p > 0, 中点在线上, y_k+1 = y_k - 1, p_k+1 = p_k + d1"""p += d1y -= 1graph_points.append((x,  y))else:"""斜率小于-1"""if point[0][1] < point[1][1]:self.swapPoint(point)# a = y2 - y1, b = x1 - x2b = point[1][0] - point[0][0]a = point[0][1] - point[1][1]# 判别参数p0 = 2 * b - a（扩大两倍）p = -2 * b + ad1 = -2 * (b - a)d2 = -2 * b# 初始点x = point[0][0]y = point[0][1]graph_points.append((x, y))while y > point[1][1]:"""y_k+1 = y_k - 1"""y -= 1if p < 0:"""if p < 0, 中点在线下, x_k+1 = x_k + 1, p_k+1 = p_k + d1"""p += d1x += 1else:"""if p > 0, 中点在线上, x_k+1 = x_k, p_k+1 = p_k + d2"""p += d2graph_points.append((x, y))def Bresenham(self, point, graph_points):"""Bresenham algorithm generate line"""dx = point[1][0] - point[0][0]dy = point[1][1] - point[0][1]m = dy / dxif m > 1:"""斜率大于1"""if point[0][1] > point[1][1]:self.swapPoint(point)delta_x = point[1][0] - point[0][0]delta_y = point[1][1] - point[0][1]# 判别参数p0 = 2 * delta_x - delta_yp = 2 * delta_x - delta_y# 初始点x = point[0][0]y = point[0][1]graph_points.append((x, y))while y < point[1][1]:"""y_k+1 = y_k + 1"""y += 1if p < 0:"""if p < 0, x_k+1 = x_k, p_k+1 = p_k + 2 * delta_x"""p += 2 * delta_xelse:"""if p > 0, x_k+1 = x_k + 1, p_k+1 = p_k + 2 * delta_x - 2 * delta_y"""p += 2 * delta_x - 2 * delta_yx += 1graph_points.append((x, y))elif m >= 0 and m <= 1:"""斜率大于0小于1"""if point[0][0] > point[1][0]:self.swapPoint(point)delta_x = point[1][0] - point[0][0]delta_y = point[1][1] - point[0][1]# 判别参数p0 = 2 * delta_y - delta_xp = 2 * delta_y - delta_x# 初始点x = point[0][0]y = point[0][1]graph_points.append((x, y))while x < point[1][0]:"""x_k+1 = x_k + 1"""x += 1if p < 0:"""if p < 0, y_k+1 = y_k, p_k+1 = p_k + 2 * delta_y"""p += 2 * delta_yelse:"""if p > 0, y_k+1 = y_k + 1, p_k+1 = p_k + 2 * delta_y - 2 * delta_x"""p += 2 * delta_y - 2 * delta_xy += 1graph_points.append((x,  y))elif m < 0 and m >= -1:"""斜率小于0大于-1"""if point[0][0] > point[1][0]:self.swapPoint(point)delta_x = point[1][0] - point[0][0]delta_y = point[1][1] - point[0][1]# 判别参数p0 = 2 * delta_y + delta_xp = 2 * delta_y + delta_x# 初始点x = point[0][0]y = point[0][1]graph_points.append((x, y))while x < point[1][0]:"""x_k+1 = x_k + 1"""x += 1if p < 0:"""if p < 0, y_k+1 = y_k - 1, p_k+1 = p_k + 2 * delta_y - 2 * delta_x"""p += 2 * delta_y + 2 * delta_xy -= 1else:"""if p > 0,  y_k+1 = y_k, p_k+1 = p_k + 2 * delta_y"""p += 2 * delta_ygraph_points.append((x,  y))else:"""斜率小于-1"""if point[0][0] > point[1][0]:self.swapPoint(point)delta_x = point[0][0] - point[1][0]delta_y = point[0][1] - point[1][1]# 判别参数p0 = -2 * delta_x - delta_yp = -2 * delta_x - delta_y# 初始点x = point[0][0]y = point[0][1]graph_points.append((x,  y))while y > point[1][1]:"""y_k+1 = y_k - 1"""y -= 1if p < 0:"""if p < 0, x_k+1 = x_k, p_k+1 = p_k - 2 * delta_x"""p -= 2 * delta_xelse:"""if p > 0, x_k+1 = x_k + 1, p_k+1 = p_k - 2 * delta_x - 2 * delta_y"""p -= 2 * delta_y + 2 * delta_xx += 1graph_points.append((x,  y))