线性代数----------学习记录
线性代数发展历程
(1)线性方程组:例如二元一次方程组;
(2)行列式:determinant,克莱默,莱布尼兹;
(3)矩阵:方程个数与未知数的个数可以不相等;
(4)线性空间,线性映射:微分方程&积分方程(calculus微积分);
特征值,内积空间,二次型-------以上是线性代数研究范围;

线性系统,叠加原理的三个基本问题(F是系统,也叫做黑箱,X是输入内容,Y是输出内容)
1.映射(map):X对应Y中的一个元素,X是定义域(domain),Y是陪域(codmain)(因为对于x,y不一定能够映射完全)(也称为像);
几种重要映射:(1)单射(单调函数)也就是一个y不能对应2个x--------对于培域里的y,存在唯一x,是的y=f(x)(2)满射:也就是每个x都能够被射到------对于培域里的y,至少存在一个x,能满足y=f(x)(3)双射:既满足单射,也满足满射
变换:定义域,陪域相同;恒同变换;记为idx,idy,即f.g=idx;f.g=idy;
-----线性映射-------
1.向量:多个实数组成的一个有序数组


冒号表示没有被定义;m维向量空间的组成(m>=1);

零维向量空间:

8条性质:


线性映射的定义:

旋转矩阵:
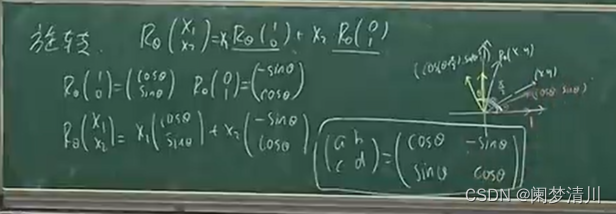
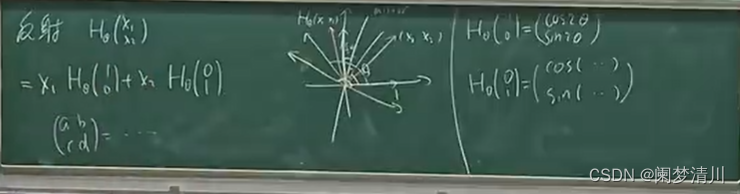


线性组合:

线性映射------>向量组----------->用矩阵进行表示
