前缀函数

π[i]=max⁡k=0,⋯,i{k∣s[0,⋯,k−1]==s[i−(k−1),⋯,i]}\pi\left[i\right] = \max\limits_{k = 0,\cdots, i}\left\{k|s\left[0,\cdots,k-1\right] == s\left[i-\left(k-1\right) ,\cdots, i\right]\right\} π[i]=k=0,⋯,imax​{k∣s[0,⋯,k−1]==s[i−(k−1),⋯,i]}
简单来说就是最长的相等的真前缀与真后缀的长度

字符串前缀函数求法

我们要求整个字符串每一个位置的前缀函数

最暴力的做法就是枚举，但是这样时间复杂度$O\left(n^3\right)$

优化

优化1
计算$\pi \left[i+1\right]$的时候，不需要从$i$枚举到$0$,可以从$\pi \left[i\right]+1$枚举到$0$
也就是说前缀函数至多增加1
证明：
由定义$s\left[0,\cdots ,\pi \left[i\right]-1\right]==s\left[i-\left(\pi \left[i\right]-1\right),\cdots ,i\right]$
并且$\forall k\ge 1,s\left[0,\cdots ,\pi \left[i\right]-1+k\right]\ne s\left[i-\left(\pi \left[i\right]-1\right)-k,\cdots ,i\right]$

如果$\pi \left[i+1\right]=\pi \left[i\right]+1+k$，其中$k\ge 1$
那么意味着$s\left[0,\cdots ,\pi \left[i\right]+k\right]==s\left[i+1-\left(\pi \left[i\right]+k+1-1\right),\cdots ,i+1\right]$
于是$s\left[0,\cdots ,\pi \left[i\right]+k-1\right]==s\left[i-\left(\pi \left[i\right]+k-1\right),\cdots ,i\right]$
矛盾

如果$s\left[\pi \left[i\right]\right]==s\left[i+1\right]$，那么$\pi \left[i+1\right]=\pi \left[i\right]+1$

优化2
如果$s\left[\pi \left[i\right]\right]\ne s\left[i+1\right]$
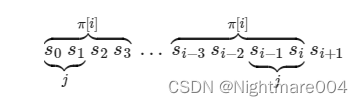
这时候我们需要找到了一个$j<\pi \left[i\right]$
使得$s\left[0,\cdots ,j-1\right]==s\left[i-j+1,\cdots ,i\right]$

由于$s\left[0,\cdots ,\pi \left[i\right]-1\right]==s\left[i-\left(\pi \left[i\right]-1\right),\cdots ,i\right]$
并且
$s\left[0,\cdots ,\pi \left[\pi \left[i\right]-1\right]-1\right]==s\left[\pi \left[i\right]-1-\left(\pi \left[\pi \left[i\right]-1\right]-1\right),\cdots ,i\right]$
也就是说$\max j=\pi \left[i\right]-1$

简单来说就是前面那一段和后面那一段是一样的，那么我们意味着前后缀也一样，那么最长的前缀就是前缀函数

所以我们的过程就是
$j^{\left(0\right)}=\pi \left[i\right]$
$j^{\left(i\right)}=\pi \left[j^{\left(i-1\right)}-1\right]$
直到$s\left[j^{\left(i\right)}\right]==s\left[i+1\right]$或者$j^{\left(i\right)}=0$
时间复杂度$O\left(n\right)$

kmp

kmp是一个字符串匹配的算法
主要原理就是，如果某一个位置不相等了，就滑到前缀和后缀相等的地方
那么求前缀和后缀相等，我们可以用前缀函数

为了方便，也可以将前缀函数整体向右移一位
因为是$i$这个位置不相等，只能找$\pi \left[i-1\right]$

代码

因为这里用的是数组，所以最好直接存一下字符串长度，不然strlen是$O\left(n\right)$

#include<cstdio>
#include<cstring>const int N = 105;
char pattern[N];//模式串
int len_p;
char text[N];//待匹配串
int len_t;
int nxt[N] = { -1 };//前缀函数void get_next() {int i = 0, j = nxt[0] = -1;while (i < len_p) {if (j == -1 || pattern[i] == pattern[j]) {++i;++j;nxt[i] = j;}else {j = nxt[j];}}
}int kmp() {int i = 0, j = 0;get_next();while (i < len_t && j < len_p) {if (j == -1 || text[i] == pattern[j]) {++j;++i;}else {j = nxt[j];}}if (j == len_p)return i - j;return -1;
}

洛谷3375

如果匹配了，那么要回到$\pi \left[le{n}_{pattern}\right]$

#include<cstdio>
#include<cstring>const int N = 1e6 + 5;
char pattern[N];//模式串
int len_p;
char text[N];//待匹配串
int len_t;
int nxt[N];//前缀函数void get_next() {int i = 0, j = nxt[0] = -1;while (i < len_p) {if (j == -1 || pattern[i] == pattern[j]) {++i;++j;nxt[i] = j;}else {j = nxt[j];}}
}void kmp() {int i = 0, j = 0;get_next();while (i < len_t) {if (j == -1 || text[i] == pattern[j]) {++i;++j;if (j == len_p) {printf("%d\n", i - j + 1);j = nxt[j];}}else {j = nxt[j];}}
}int main() {scanf("%s%s", text, pattern);len_p = strlen(pattern);len_t = strlen(text);kmp();for (int i = 1; i <= len_p; ++i) {if (i > 1)printf(" ");printf("%d", nxt[i]);}printf("\n");return 0;
}

字符串周期与border

对于字符串$s$和$0<p\le \left|s\right|$，若$s\left[i\right]==s\left[i+p\right]$对所有$i\in \left[0,\left|s-1\right|-p-1\right]$成立，则称$p$是$s$的周期

对于字符串$s$和$0\le r<\left|s\right|$，若$s$长度为$r$的前缀和长度为$r$的后缀相等，则称$s$长度为$r$的前缀是$s$的border

$s$有长度为$r$的border可以推出$\left|s\right|-r$是$s$的周期
由前缀函数，可以得到$s$所有的的border长度，即$\pi \left[\left|s\right|-1\right],\pi \left[\pi \left[\left|s\right|-1\right]-1\right],\cdots$

codeforce432D

统计每一个border出现的次数

首先求出前缀函数
接着建立一个数组$cnt$，$cnt[i]$表示$s\left[0,\cdots ,i\right]$出现的次数
初始化$cnt[i]=1$
然后从后往前遍历，$cnt[\pi \left[i\right]]+=cnt[i]$（建议自己模拟一下

#include<cstdio>
#include<cstring>
#include<stack>
using namespace std;const int N = 1e5 + 5;
char s[N];
int len_s;
int nxt[N];int cnt[N];
void get_next() {int i = 0, j = nxt[0] = -1;while (i < len_s) {if (j == -1 || s[i] == s[j]) {++i;++j;nxt[i] = j;}else {j = nxt[j];}}
}int main() {scanf("%s", s);len_s = strlen(s);get_next();fill(cnt, cnt + len_s + 1, 1);for (int i = len_s; i > 0; --i) {cnt[nxt[i]] += cnt[i];}stack<int> st;int t = len_s;while (t > 0) {st.push(t);t = nxt[t];}printf("%d\n", st.size());while (!st.empty()) {int temp = st.top();st.pop();printf("%d %d\n", temp, cnt[temp]);}return 0;
}

字符串压缩

给定一个长度为$n$得字符串$s$,我们希望找到最短得字符串$t$,使得$s=t\ast$
令$k=n-\pi \left[n-1\right]$，如果$k\mid n$，则$t=s\left[0,1,\cdots ,k\right]$就是答案
否则不存在有效的压缩

证明：
如果$k\mid n$，则字符串可以分成长度为$k$的若干块，
由前缀函数，最后一块等于倒数第二块，进而倒数第二块等于倒数第三块，以此类推
最后所有的块都是相等的

最优性证明：暂时没看懂

poj2406

#include<cstdio>
#include<cstring>const int N = 1e6 + 5;
char s[N];
int len_s;
int nxt[N];void get_next() {int i = 0, j = nxt[0] = -1;while (i < len_s) {if (j == -1 || s[i] == s[j]) {++i;++j;nxt[i] = j;}else {j = nxt[j];}}
}int main() {while (scanf("%s", s) && s[0] != '.' && s[1] != '\0') {len_s = strlen(s);get_next();int ans = len_s - nxt[len_s];if (ans == 0)printf("1\n");else if (len_s % ans == 0)printf("%d\n", len_s / ans);else printf("1\n");}return 0;
}