【算法与数据结构】343、LeetCode整数拆分
文章目录
- 一、题目
- 二、解法
- 三、完整代码
所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。
一、题目
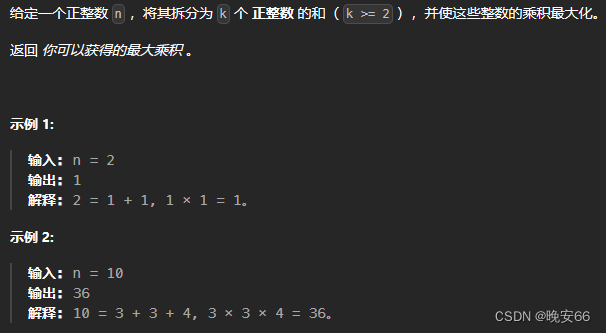
二、解法
思路分析:博主做这道题的时候一直在思考,如何找到 k k k个正整数, k k k究竟为多少合适。从数学的逻辑上来说,将 n n n均分为 k k k个数之后, k k k个数的乘积为最大(类似于相同周长下,正方形的面积大于长方形,严格的数学证明不深究了)。本题如果用动态规划的方式,令 d p [ i ] dp[i] dp[i]表示为最大的整数乘积,那么一定可以找到一个 d p [ i − j ] dp[i-j] dp[i−j],使得 d p [ i − j ] ∗ j dp[i-j]*j dp[i−j]∗j最大,并赋值给 d p [ i ] dp[i] dp[i]。而 d p [ i − j ] dp[i-j] dp[i−j]又可以进行类似操作,那么可以一直追溯到 d p [ 0 ] , d p [ 1 ] , d p [ 2 ] dp[0],dp[1],dp[2] dp[0],dp[1],dp[2]。当然,本题当中 d p [ 0 ] , d p [ 1 ] dp[0],dp[1] dp[0],dp[1]没有意义, d p [ 2 ] = 1 dp[2]=1 dp[2]=1。除了 d p [ i − j ] ∗ j dp[i-j]*j dp[i−j]∗j可以得到 d p [ i ] dp[i] dp[i]以外, ( i − j ) ∗ j (i-j)*j (i−j)∗j也可以得到 d p [ i ] dp[i] dp[i],然后我们在每次递归的过程中比较上次的 d p [ i ] dp[i] dp[i]找到最大值。因此, d p [ i ] = m a x ( d p [ i ] , m a x ( d p [ i − j ] ∗ j , ( i − j ) ∗ j ) ) dp[i]=max(dp[i], max(dp[i-j]*j, (i-j)*j)) dp[i]=max(dp[i],max(dp[i−j]∗j,(i−j)∗j))。同时,因为0和1没有意义, i i i从3开始循环,到 n n n。 j j j只要循环到 i / 2 i/2 i/2即可。
程序如下:
class Solution {
public:int integerBreak(int n) {vector<int> dp(n + 1);dp[2] = 1;for (int i = 3; i <= n; i++) {for (int j = 1; j <= i / 2; j++) {dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}}return dp[n];}
};
复杂度分析:
- 时间复杂度: O ( n 2 ) O(n^2) O(n2)。
- 空间复杂度: O ( n ) O(n) O(n)。
三、完整代码
# include <iostream>
# include <vector>
using namespace std;class Solution {
public:int integerBreak(int n) {vector<int> dp(n + 1);dp[2] = 1;for (int i = 3; i <= n; i++) {for (int j = 1; j <= i / 2; j++) {dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}}return dp[n];}
};int main() {Solution s1;int n = 10;int result = s1.integerBreak(n);cout << result << endl;system("pause");return 0;
}
end
