【高等数学之泰勒公式】
一、从零开始
1.1、泰勒中值定理1
什么是泰勒公式?我们先看看权威解读:

那么我们从古至今到底是如何创造出泰勒公式的呢?

由上图可知,任一无穷小数均可以表示成用一系列数字的求和而得出的结果,我们称之为“无穷算法”。 那么同理我们想对任一曲线来表达出其相对准确的值,则想出了与数字相同的处理方法,将曲线也表示成一系列自变量的和,这便是泰勒公式的由来。
以下我们用一组图片来更直观的了解泰勒公式的厉害之处:



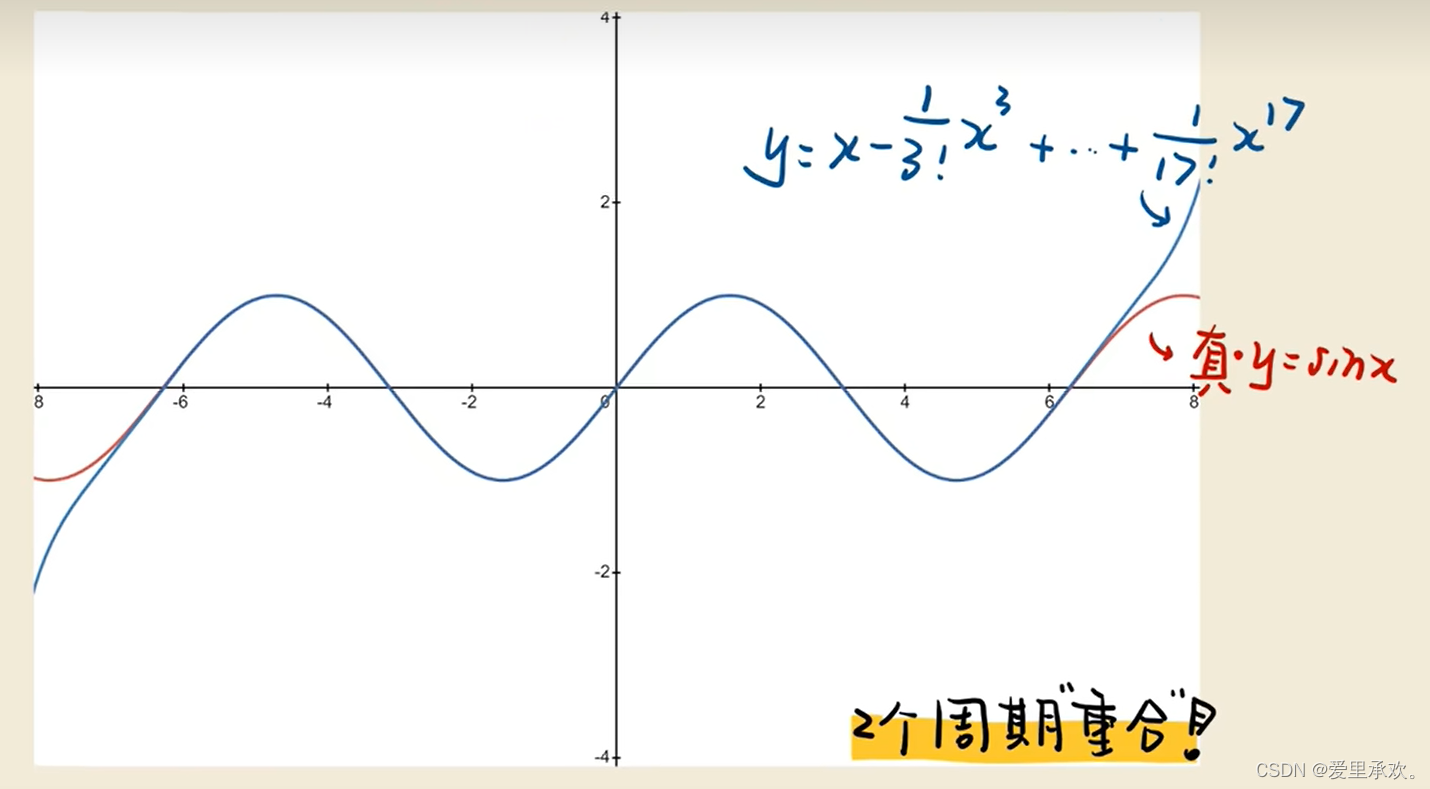
将泰勒公式展开至更高次幂则可以和目标曲线越来越接近!
1.2、寻找系数
我们通常用一个多项式来近似的表示函数f(x),而多项式中的系数就是我们破解泰勒公式的最后一道防线!




经过上面的推导,我们顺理成章的得出了f(x)的近似表达:
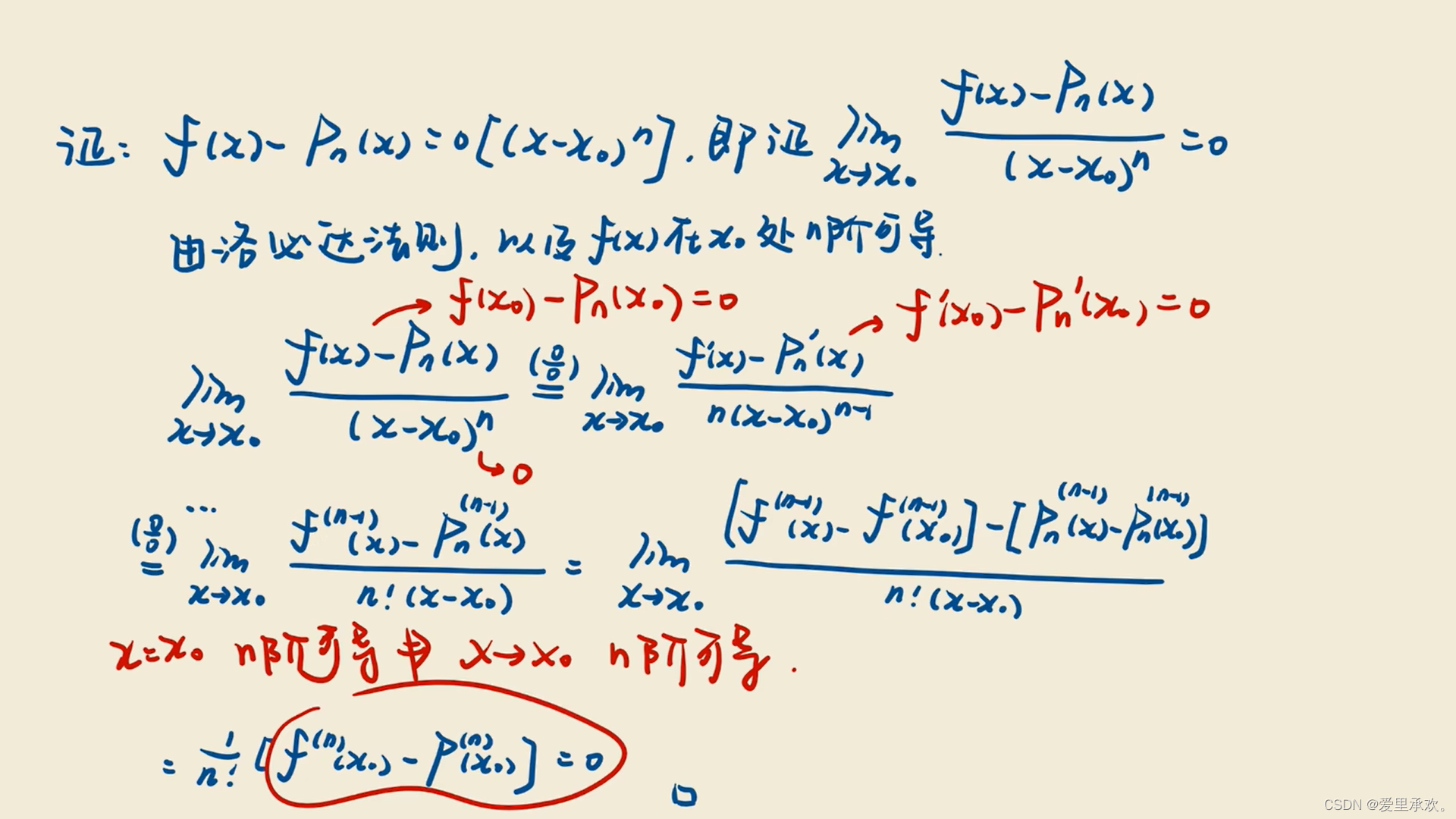
经过上面的证明,泰勒公式的基本形状已经出现,但是我们不要忘记它存在余项也就是误差项,是其前面最高次项的高阶无穷小。
1.3、泰勒中值定理2

这种形式的泰勒公式所有的条件主要是为了其中的余项来服务的,第一个公式我们只需要简单的将其写成高阶无穷小即可,而这个公式则是将余项表示的更加具体,用一个表达式来解释它。

二、常考泰勒公式



2.1、核心考点1:泰勒展开式





下面我们列出几组常用的泰勒(麦克劳林)公式展开(x -> 0):


2.2、利用泰勒公式求极限

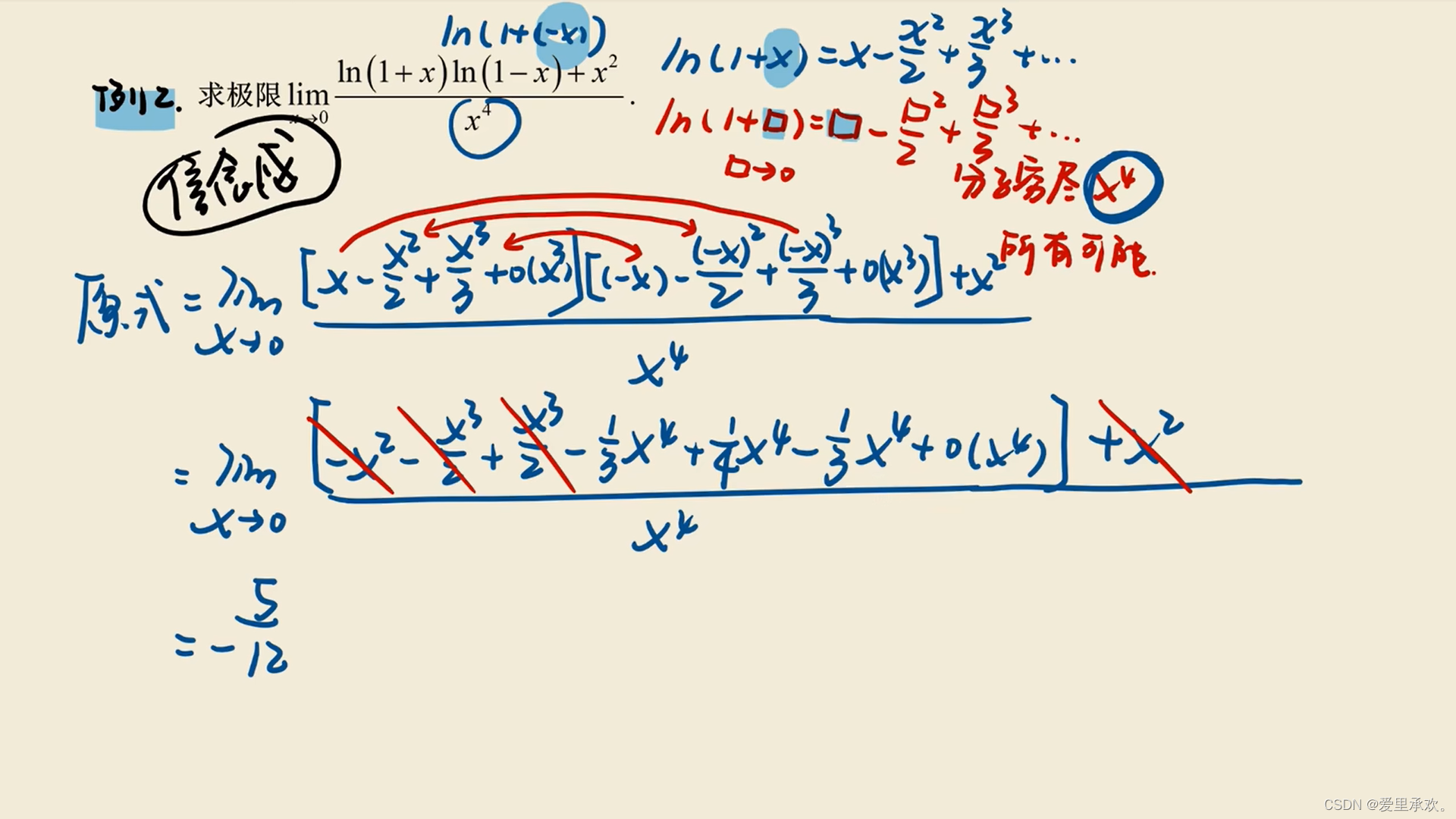
2.3、利用泰勒公式求高阶导数



2.4、利用泰勒公式解决证明题









