当前位置：首页 > news >正文

简单介绍编程进制

news 2025/8/8 5:13:42

十进制

十进制的位权为 10，比如十进制的 123，123 = 1 * 10 ^ 2 + 2 * 10 ^ 1 + 3 * 10 ^ 0。

二进制

二进制的位权为 2，比如十进制的 4，二进制为 100，4 = 1 * 2 ^ 2 + 0 * 2 ^ 1 + 0 *2 ^ 0。

Java7 之前，不支持直接写二进制值，Java7 开始支持。

int a = 0b11001;

十六进制

十六进制的位权为 16，1 个十六进制位可以理解为 4 个二进制位，比如十进制的 123，十六进制为 0x7B，123 = 7 * 16 ^ 1 + 11 * 16 ^ 0。

Java 中可以直接使用十六进制进行赋值。

int a = 0x7B；

十进制转二进制

整数部分：除 2 取余，直到商等于 0 为止，再逆序排列。

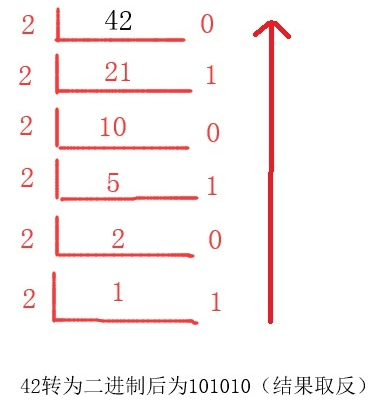
小数部分：乘 2 取整，直到积的小数部分等于 0 或者达到要求的精度，顺序排列。
最后将整数部分和小数部分合并即可。

/*比如 0.25 ，二进制为 0.01整数部分：
0 % 2 = 0 取余 0，小于 1，终止，逆序得 0小数部分：
0.25 * 2 = 0.50  取整 0
0.50 * 2 = 1.0   取整 1，小数部分为 0，终止，顺序得 01合并：
0.01*/

二进制转十进制

使用按权相加法。

/*比如 2.25，二进制为 10.012.25 = 1 * 2 ^ 1 + 0 * 2 ^ 0 + 0 * 2 ^ -1 + 1 * 2 ^ -2*/

bit 位

bit 位，计算机中表示数据的最小单位，可取 0 或 1（电路的开关）。

整数的二进制表示

任何存储于计算机中的数据，其本质都是以二进制码存储，这是由计算机硬件决定的。

根据冯·诺依曼提出的经典计算机体系结构框架，一台计算机由运算器、控制器、存储器、输入和输出设备组成。

运算器只有加法运算器，没有减法运算器（据说一开始是有的，后来由于减法运算器硬件开销太大，废弃了），所以计算机没办法直接做减法，它是通过加法间接实现的。现实中的减法也可以当成加法运算，减去一个数可以看作加上这个数的相反数。

为了表示负数，计算机引入了符号位，一般最高位（左边第一位）表示符号位，符号位为 0 表示正数，为 1 表示负数。

从硬件的角度看，只有正数加负数才算减法，正数与正数相加，负数与负数相加，都可以通过加法器直接相加。

原码

原码用第一位表示符号，其余位表示值。

byte beVar1 = 1; // 原码：0000 0001
byte beVar2 = -1; // 原码：1000 0001

反码

正数的反码等于原码，负数的反码是原码的符号位不变，其余位取反，也可以理解为它的正数原码按位取反。

byte beVar1 = 1; // 反码：0000 0001
byte beVar2 = -1; // 反码：1111 1110

补码

补码_百度百科 (baidu.com)

正数的补码等于原码，负数的补码是在反码的基础上加 1，补码取反码再加 1 又得到原码。

byte beVar1 = 1; // 补码：0000 0001
byte beVar2 = -1; // 补码：1111 1111

理解补码

8 bit 位为例，取值范围为 0000 0000 ~ 1111 1111，1111 1111 加 1 后变成 1 0000 0000，由于只有 8 位，溢出的 1 要舍弃，只能保留 0000 0000。

即 1111 1111 加 0000 0001 变成了 0000 0000，也就是说，1111 1111 等同 -1，同理可得 1111 1110 等同 -2，…… 1000 0000 等同 -128。

补码的思想类似时钟，如下图（为了类比，将 12 点改成了零点），值在 0 ~ 11 之间，10 点等同 -2 点。

类似这样有计数范围的系统都存在一个“模”，如：时钟的计量范围是 0~11，模=12。“模”实质上是计量器产生“溢出”的量，它的值在计量器上表示不出来，计量器上只能表示出模的余数。任何有模的计量器，均可化减法为加法运算。

小数的二进制表示

二进制中为表示小数，采用类似十进制的科学计数法，几乎所有的硬件和编程语言表示小数的二进制格式都是使用 IEEE 754 标准。

小数 = [符号位] [指数部分] . [小数部分]
32 位单精度二进制 = [1 个符号位] [8 个阶码位] [23 个尾数位]
64 位双精度二进制 = [1 个符号位] [11 个阶码位] [52 个尾数位]
8 位阶码位移码偏移量 127，11 位阶码位移码偏移量 1023

单精度

双精度

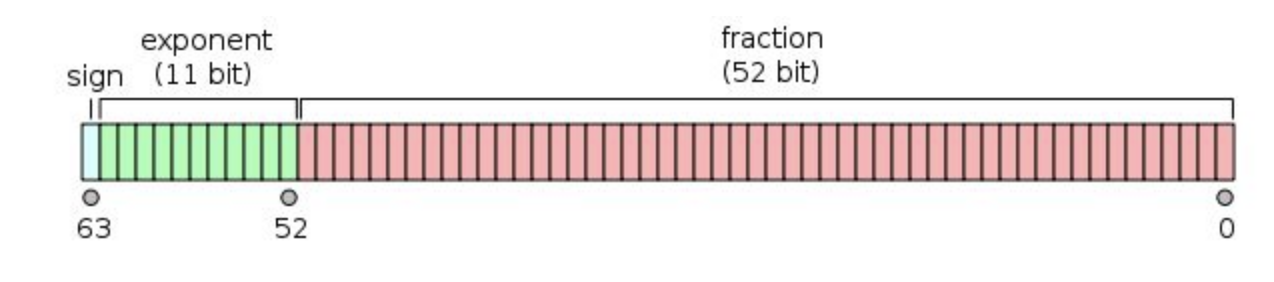
/*如：2.25，二进制 10.01，先化为科学计数法 1.001 * （2 ^ 1）1.001 * （2 ^ 1）的 32 位单精度表示：符号位： 0阶码位：阶码 = 指数 + 阶码位移码偏移量 = 1 + 127 = 128，二进制 1000 0000尾数位：尾数 = 取小数点后 23 位，001 0000 0000 0000 0000 0000最终得：[0][1000 0000][001 0000 0000 0000 0000 0000]同理可得 -2.25 的二进制：[1][1000 0000][001 0000 0000 0000 0000 0000]*/public static void main(String[] args) {System.out.println(Integer.toBinaryString(Float.floatToIntBits(2.25F)));System.out.println(Integer.toBinaryString(Float.floatToIntBits(-2.25F)));
}