揭露欧拉骗局第二篇：逼近公式“Σ1/n=lnn+C”。
Σ1/n=lnn+C是欧拉为调和级数创造(注意是创造、而不是发现)的“逼近公式”，它在欧系大名鼎鼎，因为它解决了欧洲人百筹莫展的“调和级数求和问题”。
“lnn+C”是欧拉的发明，欧拉认为n→∞时，Σ1/n=lnn+常数，这个常数就是欧拉常数C=0.5772156649…。当欧拉发现以10倍率对Σ1/n翻倍分项、分项值会收敛至常数2.30258509、恰恰吻合ln10(其实彼此有差值，但欧拉习惯打马虎眼)以后，他就采用绑架换梁法——用lnn绑架Σ1/n“持续翻倍”、实现lnn替代Σ1/n，从而获得“Σ1/n=lnn+C”，——两个毫无瓜葛的变量因为一个常数变成等量，这个哄鬼瞎话数学人居然都信了！虽然没有任何n值能让Σ1/n=lnn+C成立，但它却成了欧系最著名数学公式之一。欧拉是拿观众当白 痴，诡异的是数学界真的就成了白 痴，没有人指责欧拉胆大妄为，反而都对着鬼话唱赞美歌，他们说n=1.2.3.时不成立，n→∞就成立了。一代代数学人自此面对Σ1/n、在n值“很大的时候(通常＞1000000)”就用“lnn+C”顶缸，目前电脑编程采用的就是该方法顶缸，也就是说你求1+1/2+1/3+…+1/2543578618904487，电脑出来的是ln2543578618904487+0.5772156499…。这种恬不知耻的欺诈行为，始作俑者就是欧拉。
欧拉是纯粹数学旗帜，他的谬论构成纯数框架
学过数学的人都知道y=x+C是“平行线(平移函数)”关系，即y是x平移C个点位；C通常是有理数，如果C是无理数，那么y或者x的变量必然都存在取集限制，如此才会产生“无限趋近永不相交”情形。回看Σ1/n=lnn+C，第一眼可得“Σ1/n是lnn平移C个点位”，进一步了解C是无理数，那么Σ1/n与lnn必定是变量受到了取集限制。然而事实不然，Σ1/n与lnn取集完全相同、并无任何限制，故由趋势不可改变理论可以判定：不是平移函数的Σ1/n与lnn必定相交、彼此间不可能存在无理数常量差，也就是说“常数C”是欧拉捏造的，Σ1/n与lnn+C之间绝对画不上等号。
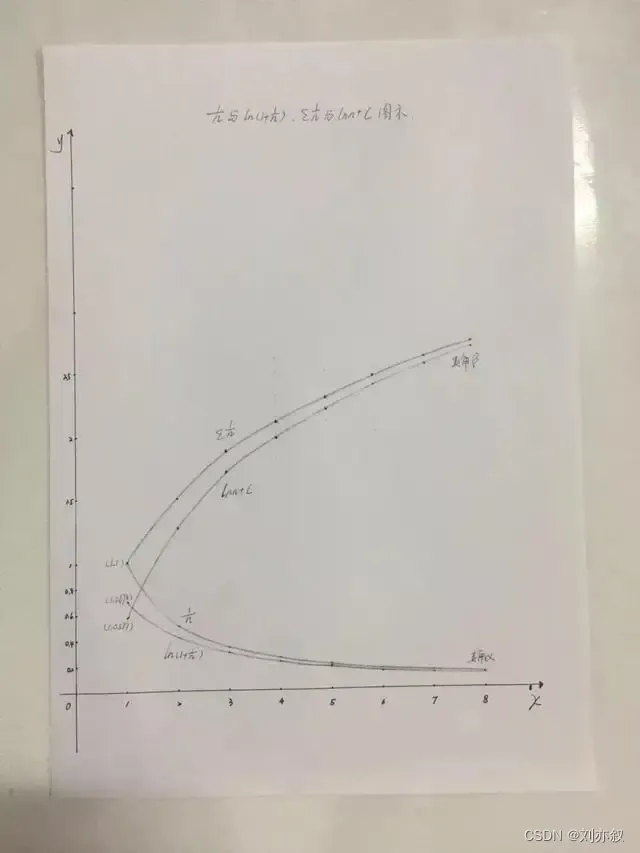1/n与ln（1+1/n）、Σ1/n与lnn+C趋势必定相交
再来看Σ1/n、lnn与它们的子项1/n、ln(1+1/n)。Σ1/n是1/n的无限累加，lnn是ln(1+1/n)的无限积分，彼此之间的关系是风马牛毫不相干；1/n→0，ln(1+1/n)→常数，如果Σ1/n＞lnn，则0＞常数成立，这显然不可能，从这里也能证明Σ1/n=lnn+C荒诞无稽。
没有任何证据能证明Σ1/n=lnn+C成立
Σ1/n=lnn+C从未经过任何证明，它是在欧拉的威名下变成的“公式”的；欧洲人之所以在这个问题上浮皮潦草，一方面是出于对欧拉的忌惮，另一方面是Σ1/n在欧系数学特别重要、但欧洲人长期找不到解决方案，既然Σ1/n=lnn+C能解决Σ1/n问题，大家自然没有二话，也因此李鬼等式及欧拉常数总是被描绘得神秘又高贵、艰涩又诡妙，让数学人的膝盖不由自主地发软。而真实的李鬼等式简单得只需一句话就能概括：用lnn绑架Σ1/n、以x翻倍分级，彼此的差值为欧拉常数，循环论证即为Σ1/n=lnn+C，秘笈只在于用让Σ1/n翻倍分级，使其与k*lnx同步起伏。
戳破欧拉常数和Σ1/n=lnn+C非常简单：画个坐标草图就能发现Σ1/n的收敛速度大过lnn、证明“Σ1/n以x翻倍分项级数=lnx”不成立；使用最简单的硬算法，至迟n=9890128，lnn+C就会上穿Σ1/n、令“欧拉常数”破产、令李鬼等式现形(有兴趣者可以实算验证，只要是硬算而不是编程，分分钟可以证明欧拉造假作弊)。
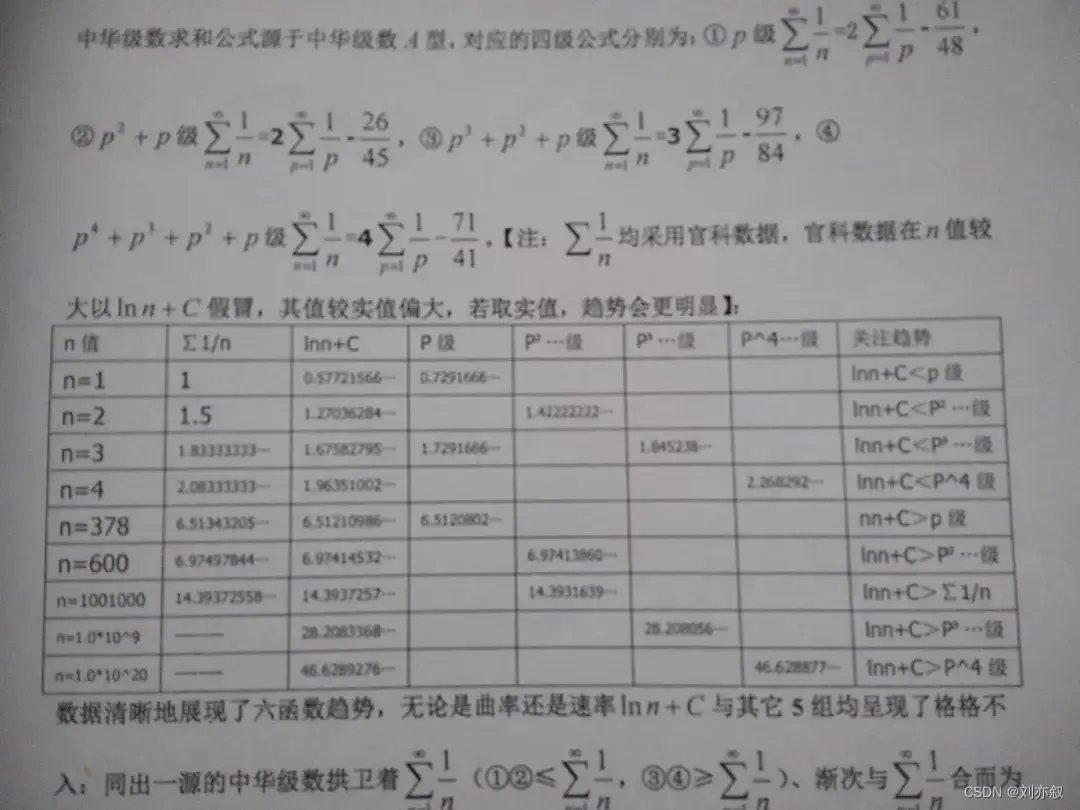Σ1/n有多种直算方法
李鬼等式Σ1/n=lnn+C能在数学界堂而皇之，仰仗的除了欧拉的大名，还有它的无从证伪，它让人类数学走了几百年弯路，空耗了人类的无限才智带来的却全是负能量。
邀你讨论
欧拉常数公式的证明很难
吗?说说你的看法
去发布