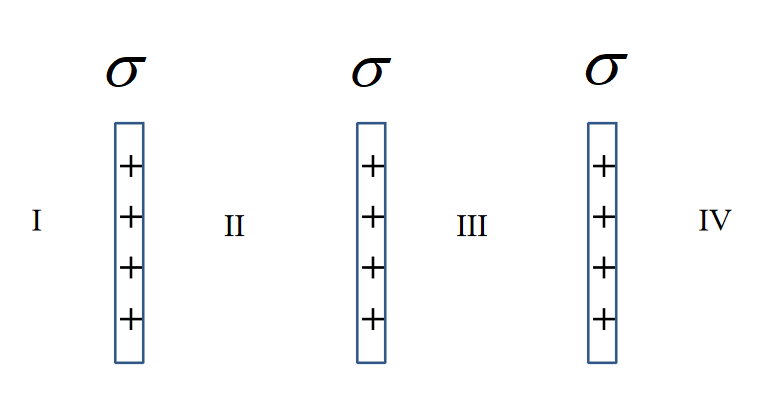大学物理II-作业1【题解】
1.【单选题】——考查高斯定理
下面关于高斯定理描述正确的是(D )。
A.高斯面上的电场强度是由高斯面内的电荷激发的
B.高斯面上的各点电场强度为零时,高斯面内一定没有电荷
C.通过高斯面的电通量为零时,高斯面上各点电场强度必为零
D.通过高斯面的电通量仅由高斯面内的电荷决定
选项A:总电场强度,是由高斯面(闭合曲面)内外的电荷激发的;
选项B:错,应该是电荷的代数和为0 ,根据这个是无法断定高斯面内没有电荷的。
选项C:不一定,通过高斯面的电通量为0时,只能说明高斯面内电荷的代数和为0 ,而电场强度不仅受面内的电荷影响,还受面外的电荷影响。
选项D:是的,电通量是由高斯面内的电荷决定的,与高斯面外的电荷无关
2、【单选题】——电场线

这道题,不好评,就当是知识点温故。但凡高中有听过一节电场课的都能做对。
选项A:正电荷源场,向外发散
选项B:负电荷汇场,向里聚集
选项C:电场线有头有尾,始于正电荷终于负电荷,不是闭合曲线
选项D:电场线不会相交
3.【判断题】 ——电场强度
静电场中某点的电场强度与试验电荷0q 的大小和正负均有关。( 错)
回到电场强度的定义式:
(E和F是矢量有方向的,打不出箭头)
试验电荷存在与否都与电场强度无关
4.【判断题】——电通量
通过闭合曲面的电场线,若是穿进曲面,则电通量为正;若是穿出曲面,则电通量为负。( 错)
穿进为负,穿出为正,可以画图辅助理解。
5.【判断题】——电势零点
电场中某点的电势值与电势零点选取有关,而任意两点的电势差与电势零点的选取无关。( 对)
因为电势零点的选取是任意的,所以电场中某点的电势值与其选取有关。电势差是一个相对量,电势零点不管怎么变,任意两点的电势差都不受影响。
6.【判断题】——静电屏蔽
空腔导体只有接地后,才能使腔内的空间不受外界电场的影响。( 错)
空腔导体不管接地与否,腔内空间都不会受外界电场的影响。
但是若想让腔内空间不受内电场影响,那么就需要接地。
- 只屏蔽外电场,不屏蔽内电场,是可以的,只要使这个空腔导体不接地就可以了。
- 只屏蔽内电场,不屏蔽外电场,是不行的。
7.【判断题】——电容
平行板电容器的电容与极板的面积成反比,与极板的距离成正比。( 错)
(1)这里注意电容的定义式:
,其大小与导体的形状、相对位置、其间的电介质有 关,与其所带的电荷量无关。
(2)而平行板的电容
,与面积成正比,与距离成反比
8.【填空题】——电场强度定义式
电场中某点处的电场强度等于位于该点的单位正试验电荷所受的__电场力_。
电场强度的定义式:
(E和F是矢量有方向的,打不出箭头)
9.【填空题】——静电场的环路定理
静电场中,某试验电荷沿着闭合路径移动一周,则电场力做功为__0_。
在静电场中,电场强度 E 沿任意闭合路径的线积分为零。
10.【填空题】——电势的定义式
电场中某点的电势等于单位正电荷在该点所具有的__电势能_。
11.【填空题】——静电平衡的条件
导体处于静电平衡时,导体内部任一点的电场强度为__0_;
导体表面处电场强度方向都与导体表面_垂直__;
导体上的电势处处__相等_。
12.【填空题】——电势梯度
静电场中电势为常量的区域,其电场强度为__0_。
电场中某一点的电场强度沿任一方向的分量,等于这一 点的电势沿该方向电势变化率的负值。
13.【填空题】——电场强度叠加原理
点电荷系所激发的电场中某点处的电场强度等于各个点电荷单独存在时对该点所激发的电场强度的_矢量和__。
14.【填空题】——电势的叠加原理
点电荷系所激发的电场中某点的电势等于各个点电荷单独存在时在该点建立的电势的代数和。
15.【填空题】——电容的串并联
当两个电容器_并联__时,其等效电容等于这两个电容器的电容之和。
并联:
串联:

16.【填空题】——电场能量密度公式
电场的能量密度与电场强度的二次方成__正比_。
17.【填空题】——无限大均匀带电平行平面求电场强度
如图,三块“无限大”均匀带电平行平面,试求空间各区域的电场强度?(规定向右为电场强度的正方向)