三角函数两角和差公式推导
一.几何推理
1.两角和公式
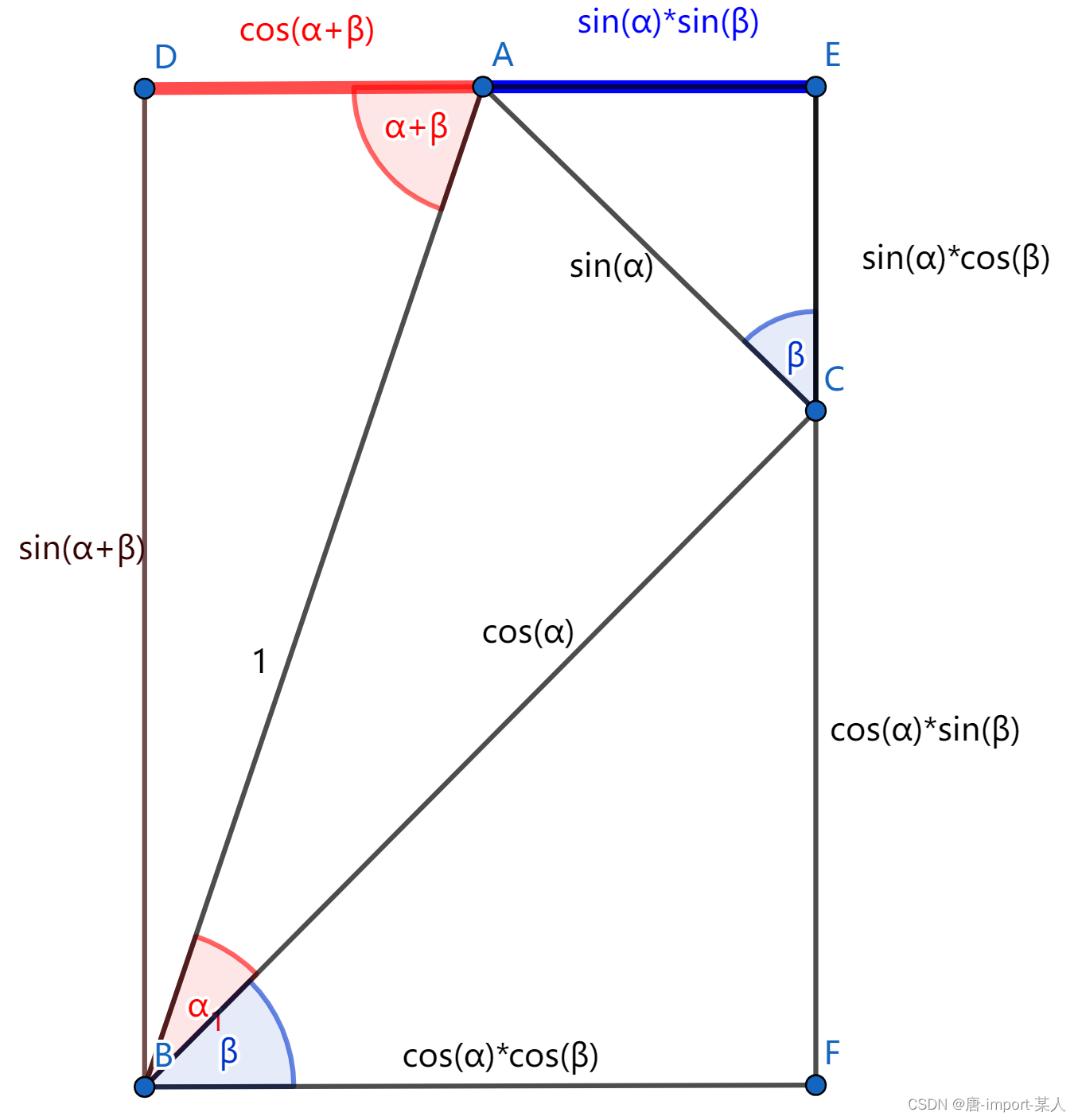
做一斜边为1的直角△ABC,任意旋转非 k Π , k = N kΠ,k=N kΠ,k=N,补充如图,令 ∠ A B C = ∠ α , ∠ C B F = ∠ β ∠ABC=∠α,∠CBF=∠β ∠ABC=∠α,∠CBF=∠β
∴ ∠ D B F = ∠ D B A + ∠ α + ∠ β = 90 ° , ∠ D A F = ∠ D B A + ∠ D A B ∴∠DBF=∠DBA+∠α+∠β=90°,∠DAF=∠DBA+∠DAB ∴∠DBF=∠DBA+∠α+∠β=90°,∠DAF=∠DBA+∠DAB
∵ ∠ D A B = ∠ α + ∠ β ∵∠DAB=∠α+∠β ∵∠DAB=∠α+∠β
∴ ∠ A C F + ∠ B C F = 90 ° ∴∠ACF+∠BCF=90° ∴∠ACF+∠BCF=90°
∵ ∠ A C F = ∠ β ∵∠ACF=∠β ∵∠ACF=∠β
∴ A B 长度为 1 ∴AB长度为1 ∴AB长度为1
∵ A C = s i n ( α ) , B C = c o s ( α ) ∵AC=sin(α),BC=cos(α) ∵AC=sin(α),BC=cos(α)
∵ B F = c o s ( α ) ∗ c o s ( β ) , C F = c o s ( α ) ∗ s i n ( β ) , A E = s i n ( α ) s i n ( β ) , C E = s i n ( α ) c o s ( β ) , B D = E F = s i n ( α + β ) , D A = c o s ( α + β ) ∵BF=cos(α)*cos(β),CF=cos(α)*sin(β),AE=sin(α)sin(β),CE=sin(α)cos(β),BD=EF=sin(α+β),DA=cos(α+β) ∵BF=cos(α)∗cos(β),CF=cos(α)∗sin(β),AE=sin(α)sin(β),CE=sin(α)cos(β),BD=EF=sin(α+β),DA=cos(α+β)
∵ { c o s ( α + β ) = c o s ( α ) ∗ c o s ( β ) − s i n ( α ) ∗ s i n ( β ) s i n ( α + β ) = s i n ( α ) ∗ c o s ( β ) + c o s ( α ) ∗ s i n ( β ) ∵\begin{cases} cos(α+β)=cos(α)*cos(β)-sin(α)*sin(β) \\sin(α+β)=sin(α)*cos(β)+cos(α)*sin(β) \end{cases} ∵{cos(α+β)=cos(α)∗cos(β)−sin(α)∗sin(β)sin(α+β)=sin(α)∗cos(β)+cos(α)∗sin(β)
2.两角差公式
∵ { c o s ( α + β ) = c o s ( α ) ∗ c o s ( β ) − s i n ( α ) ∗ s i n ( β ) s i n ( α + β ) = s i n ( α ) ∗ c o s ( β ) + c o s ( α ) ∗ s i n ( β ) ∵\begin{cases} cos(α+β)=cos(α)*cos(β)-sin(α)*sin(β) \\sin(α+β)=sin(α)*cos(β)+cos(α)*sin(β) \end{cases} ∵{cos(α+β)=cos(α)∗cos(β)−sin(α)∗sin(β)sin(α+β)=sin(α)∗cos(β)+cos(α)∗sin(β)
对 ∠ β 做取反变化 对∠β做取反变化 对∠β做取反变化
∵ { c o s ( α + ( − β ) ) = c o s ( α ) ∗ c o s ( β ) − s i n ( α ) ∗ ( − s i n ( β ) ) s i n ( α + ( − β ) ) = s i n ( α ) ∗ c o s ( β ) + c o s ( α ) ∗ ( − s i n ( β ) ) ∵\begin{cases} cos(α+(-β))=cos(α)*cos(β)-sin(α)*(-sin(β)) \\sin(α+(-β))=sin(α)*cos(β)+cos(α)*(-sin(β)) \end{cases} ∵{cos(α+(−β))=cos(α)∗cos(β)−sin(α)∗(−sin(β))sin(α+(−β))=sin(α)∗cos(β)+cos(α)∗(−sin(β))
∵ { c o s ( α − β ) = s i n ( α ) ∗ s i n ( β ) + c o s ( α ) ∗ s i n ( β ) s i n ( α − β ) = s i n ( α ) ∗ c o s ( β ) − c o s ( α ) ∗ s i n ( β ) ∵\begin{cases} cos(α-β)=sin(α)*sin(β)+cos(α)*sin(β) \\sin(α-β)=sin(α)*cos(β)-cos(α)*sin(β) \end{cases} ∵{cos(α−β)=sin(α)∗sin(β)+cos(α)∗sin(β)sin(α−β)=sin(α)∗cos(β)−cos(α)∗sin(β)
3.总结
∵ { c o s ( α + β ) = c o s ( α ) ∗ c o s ( β ) − s i n ( α ) ∗ s i n ( β ) s i n ( α + β ) = s i n ( α ) ∗ c o s ( β ) + c o s ( α ) ∗ s i n ( β ) c o s ( α − β ) = s i n ( α ) ∗ s i n ( β ) + c o s ( α ) ∗ s i n ( β ) s i n ( α − β ) = s i n ( α ) ∗ c o s ( β ) − c o s ( α ) ∗ s i n ( β ) ∵\begin{cases} cos(α+β)=cos(α)*cos(β)-sin(α)*sin(β) \\sin(α+β)=sin(α)*cos(β)+cos(α)*sin(β) \\cos(α-β)=sin(α)*sin(β)+cos(α)*sin(β) \\sin(α-β)=sin(α)*cos(β)-cos(α)*sin(β) \end{cases} ∵⎩ ⎨ ⎧cos(α+β)=cos(α)∗cos(β)−sin(α)∗sin(β)sin(α+β)=sin(α)∗cos(β)+cos(α)∗sin(β)cos(α−β)=sin(α)∗sin(β)+cos(α)∗sin(β)sin(α−β)=sin(α)∗cos(β)−cos(α)∗sin(β)
4.其他
为什么几何推理∠β和∠α不是钝角,根据诱导公式可将钝角化为锐角。所以只推导锐角和可以等价于推导任意角和
