LC-70-爬楼梯
原题链接:爬楼梯
个人解法
思路:
动态规划
状态表示:f[i]表示走到第n阶台阶有几种方法
状态转移:f[i] = f[i -1] + f[i - 2]
这实际上就是斐波那契数列,通过转移可以看到,我们只用了三个变量,故可以不用状态数组,而只用三个变量进行转移。
时间复杂度:O(n)O(n)O(n)
代码:
class Solution {
public:int climbStairs(int n) {int a = 1, b = 1, c = 1;for(int i = 2;i <= n;i ++) {c = a + b;a = b, b = c;}return c;}
};
更好的解法
- 斐波那契数列矩阵表示

由递推可以得到:
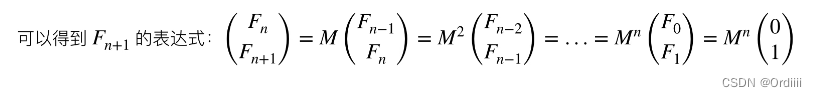
故我们可以利用矩阵乘法快速幂求出MnM^nMn,从而求除FnF_nFn
- 利用解析解
斐波那契数列解析解:
由矩阵表示可以看到MMM矩阵为可逆矩阵且MMM可相似对角化,从而表示为M=SΛS−1,其中Λ为由特征值,S为特征向量组成的矩阵M = S\Lambda S^{-1},其中\Lambda为由特征值,S为特征向量组成的矩阵M=SΛS−1,其中Λ为由特征值,S为特征向量组成的矩阵
那么Mn=SΛnS−1,从而求出Fn的解析解那么M^n = S\Lambda^{n}S^{-1},从而求出F_n的解析解那么Mn=SΛnS−1,从而求出Fn的解析解
