leetcode——打家劫舍问题汇总
本章汇总一下leetcode中的打家劫舍问题,使用经典动态规划算法求解。
1、梦开始的地方——打家劫舍(★)

本题关键点就是不能在相邻房屋偷东西。
采用常规动态规划做法:
- 根据题意设定dp数组,dp[i]的含义为:前i个房屋内,能偷的最高金额。
- 需要初始化dp[0]=0,dp[1]=nums[0]。
- 遍历dp数组,对应两种情况:偷或者不偷。 递推公式为:
-
dp[i] = Math.max(dp[i-1] , dp[i-2]+nums[i-1]);
-
-
最后返回dp数组最后一个数。
java代码如下:
class Solution {public int rob(int[] nums) {if(nums.length == 1) return nums[0];int[] dp = new int[nums.length+1]; //dp[i]:前i个房屋内,能偷的最高金额。dp[1] = nums[0];for(int i=2; i<=nums.length; i++){dp[i] = Math.max(dp[i-1] , dp[i-2]+nums[i-1]); //分别对应偷或者不偷}return dp[nums.length];}
}2、打家劫舍II

本题是上一题的进阶版,区别在于收尾两个房屋也是相邻的,不能同时偷。 此时无非就两种情况:
- 不偷首房屋。
- 不偷尾房屋。
分别设两个dp数组对应以上两种情况即可,思路还是类似上一题。
java代码如下:
class Solution {public int rob(int[] nums) {if(nums.length == 1) return nums[0];int[] dp1 = new int[nums.length]; //不偷首房屋int[] dp2 = new int[nums.length]; //不偷尾房屋dp1[1] = nums[1];dp2[1] = nums[0];for(int i=2; i<nums.length; i++){dp1[i] = Math.max(dp1[i-1] , dp1[i-2]+nums[i]);dp2[i] = Math.max(dp2[i-1] , dp2[i-2]+nums[i-1]);}return dp1[nums.length-1] > dp2[nums.length-1] ? dp1[nums.length-1] : dp2[nums.length-1];}
}3、打家劫舍III(★)
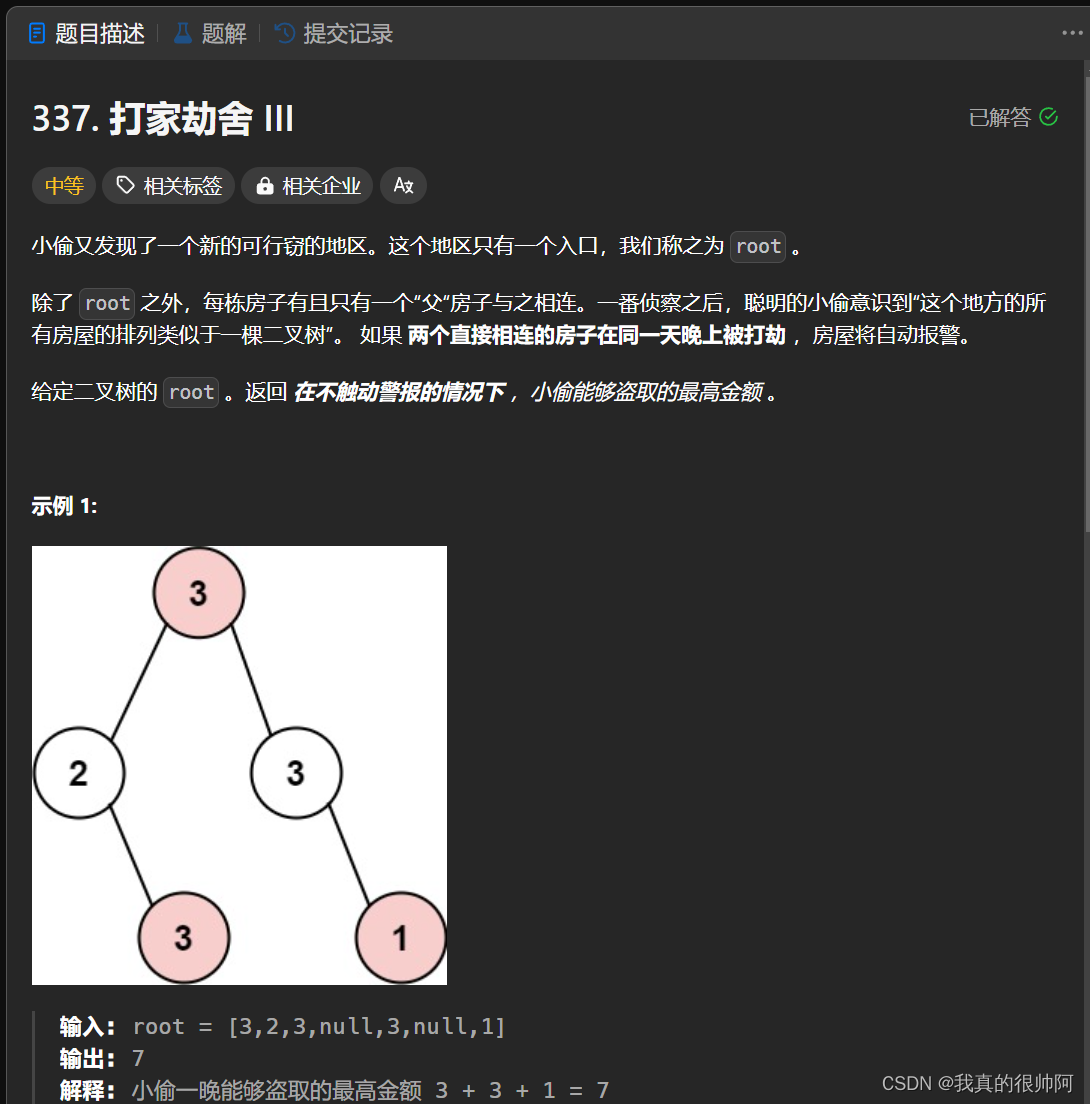
本题是从数组型dp转化为树形dp,由于父节点的状态需要从孩子节点的状态推出来,因此需要使用后序遍历。
首先需要定义一个递归函数dfs,参数为当前节点,返回值为长度为2的数组,即dp数组,dp[0]代表选当场节点,dp[1]代表不选当前节点。 如下:
int[] dfs(TreeNode node)
接下来确定终止条件:
if(node == null) return new int[] {0,0};
使用后序遍历递归遍历左右子树:
//递归左右子树
int[] left = dfs(node.left);
int[] right = dfs(node.right);
确定单层递归逻辑:
//分别对应偷与不偷的情况:
int rob = node.val + left[1] + right[1];
int no_rob = Math.max(left[0],left[1]) + Math.max(right[0],right[1]);
java代码如下:
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int rob(TreeNode root) {int[] ans = dfs(root);return Math.max(ans[0],ans[1]);}private int[] dfs(TreeNode node){if(node == null) return new int[] {0,0};//递归左右子树int[] left = dfs(node.left);int[] right = dfs(node.right);int rob = node.val + left[1] + right[1];int no_rob = Math.max(left[0],left[1]) + Math.max(right[0],right[1]);return new int[] {rob,no_rob};}
}
