7 线性回归及Python实现
1 统计指标
- 随机变量XXX的理论平均值称为期望: μ=E(X)\mu = E(X)μ=E(X)
- 但现实中通常不知道μ\muμ, 因此使用已知样本来获取均值
X‾=1n∑i=1nXi.\overline{X} = \frac{1}{n} \sum_{i = 1}^n X_i. X=n1i=1∑nXi. - 方差variance定义为:
σ2=E(∣X−μ∣2).\sigma^2 = E(|X - \mu|^2). σ2=E(∣X−μ∣2). - 用已知样本的数据来代替:
S2=Var(X)=1n∑i=1n(Xi−μ)2.S^2 = Var(X) = \frac{1}{n} \sum_{i = 1}^n (X_i - \mu)^2. S2=Var(X)=n1i=1∑n(Xi−μ)2. - 由于μ\muμ未知, 使用贝塞尔校正:
S2=Var(X)=1n−1∑i=1n(Xi−X‾)2.S^2 = Var(X) = \frac{1}{n - 1} \sum_{i = 1}^{n} (X_i - \overline{X})^2. S2=Var(X)=n−11i=1∑n(Xi−X)2. - 原因: 在已知数据上, 使用X‾\overline{X}X获得的结果一般更小:
∑i=1n−1(Xi−X‾)2≤∑i=1n−1(Xi−μ)2.\sum_{i = 1}^{n - 1} (X_i - \overline{X})^2 \leq \sum_{i = 1}^{n - 1} (X_i - \mu)^2. i=1∑n−1(Xi−X)2≤i=1∑n−1(Xi−μ)2. - 更多解释: https://www.zhihu.com/question/20099757
- 标准差:
σX=S=Var(X).\sigma_X = S = \sqrt{Var(X)}. σX=S=Var(X).
偏差与方差:
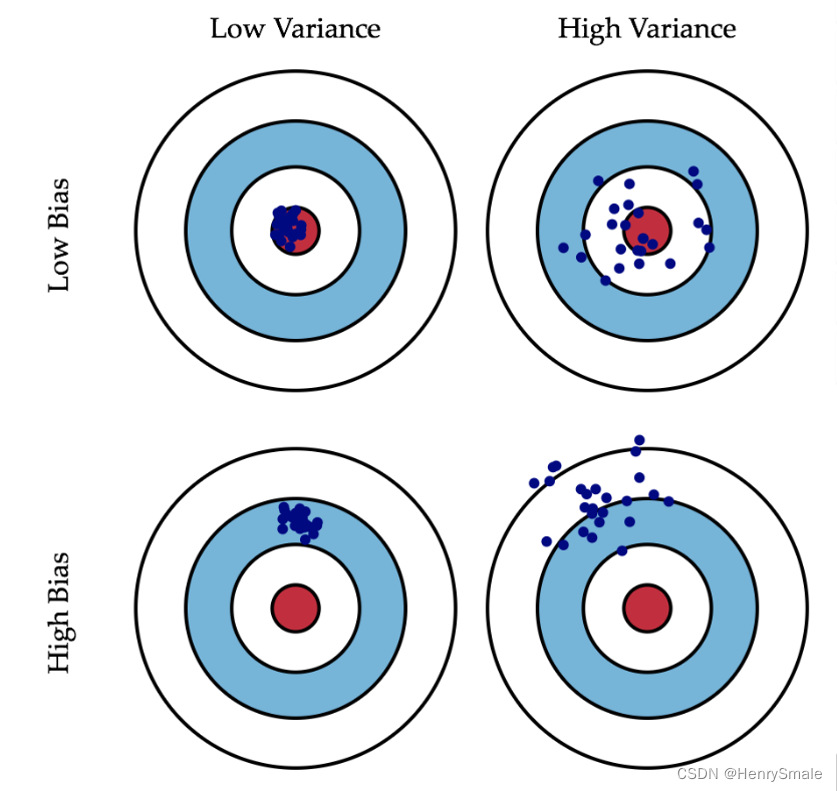
- 方差(again)
Var(X)=σX2=1n−1∑i=1n(Xi−X‾)(Xi−X‾).Var(X) = \sigma_X^2 = \frac{1}{n - 1} \sum_{i = 1}^{n} (X_i - \overline{X})(X_i - \overline{X}). Var(X)=σX2=n−11i=1∑n(Xi−X)(Xi−X). - 协方差
Cov(X,Y)=1n−1∑i=1n(Xi−X‾)(Yi−Y‾).Cov(X, Y) = \frac{1}{n - 1} \sum_{i = 1}^{n} (X_i - \overline{X})(Y_i - \overline{Y}). Cov(X,Y)=n−11i=1∑n(Xi−X)(Yi−Y). - Pearson相关系数
Corr(X,Y)=ρX,Y=Cov(X,Y)σXσY.Corr(X, Y) = \rho_{X, Y} = \frac{Cov(X, Y)}{\sigma_X \sigma_Y}. Corr(X,Y)=ρX,Y=σXσYCov(X,Y).
2 线性回归
2.1 回归任务
分类与回归
- 分类任务预测类别,即是/否等离散值:如是否生病;
- 回归任务预测实型值:如气温
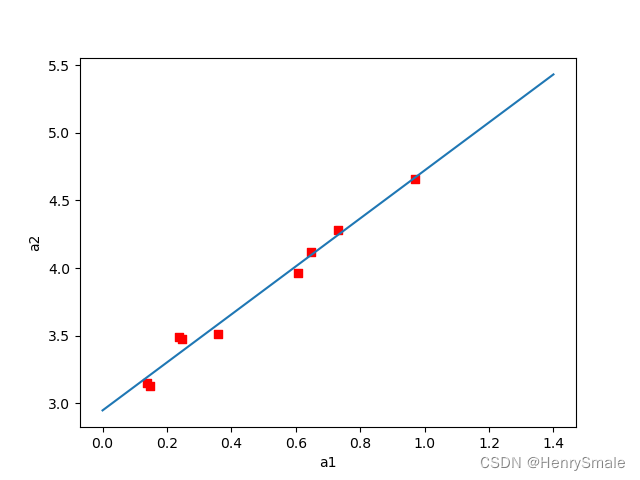
拟合空间中的点 (注意数据点没有类别标记, 输出也占一维):
- 一个条件属性:直线;
- 两个条件属性:平面;
- 更多条件属性:超平面.
拟合线: