由正规表达式构造DFA,以及DFA的相关化简
目录
1.由正规式到DFA
首先讲如何从正规式到NFA
如何从NFA到DFA
2.DFA的化简
3.DFA和NFA的区别
1.由正规式到DFA
正规式--->NFA---->DFA
首先讲如何从正规式到NFA
转换规则:

例题1:这里圆圈里面的命名是随意的,只要能区别开就可以了

如何从NFA到DFA
NFA---->状态转换表---->状态转换矩阵---->DFA
如下例题: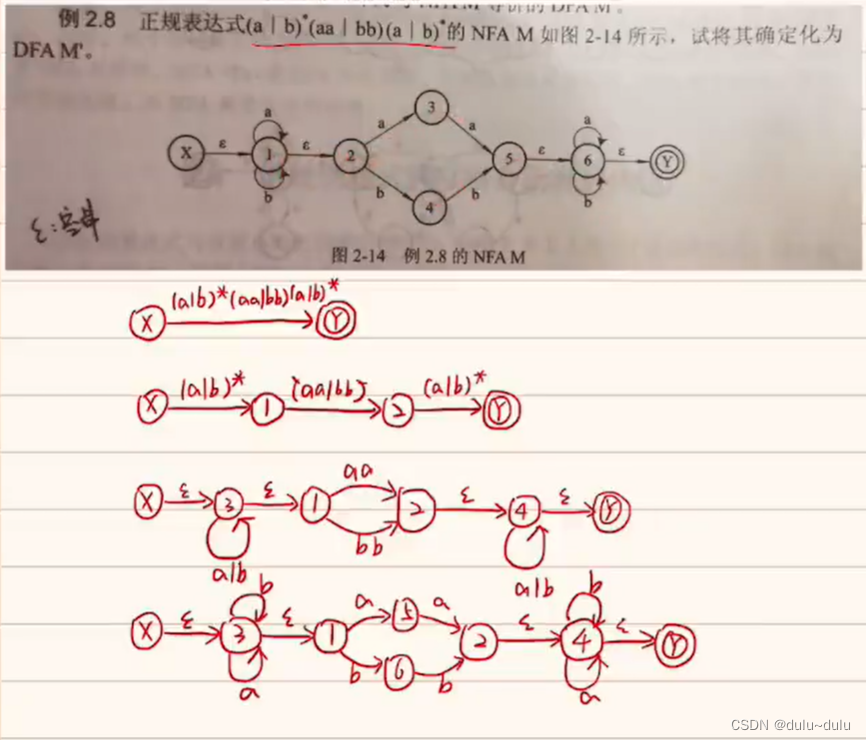
以上NFA的转换表如下图所示:
这里的"I"是从x出发的状态,"Ia"表示I集合中的字符经过a的状态的集合
规则:若经过的是(空串),那么就经过空串后到达的字符加入到集合中,如果没有经过
空串,就不到达。
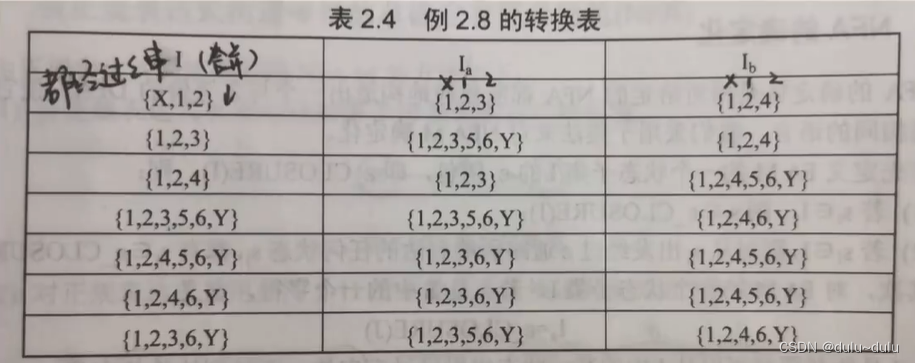
这里的每一列就是列举上一行中出现的集合,例如第二列,列举的就是上一行中出现的红框的集合

就拿I={1,2,3}具体说:
由图,1经过a的状态有:1,2经过a的状态有3,3经过a的状态有5,6,Y(因为5后面接的就是串),所以
={1,2,3,5,6,Y}

以此类推就能得到转换表,再将相同的集合表示出来

就可以进一步得到转换矩阵
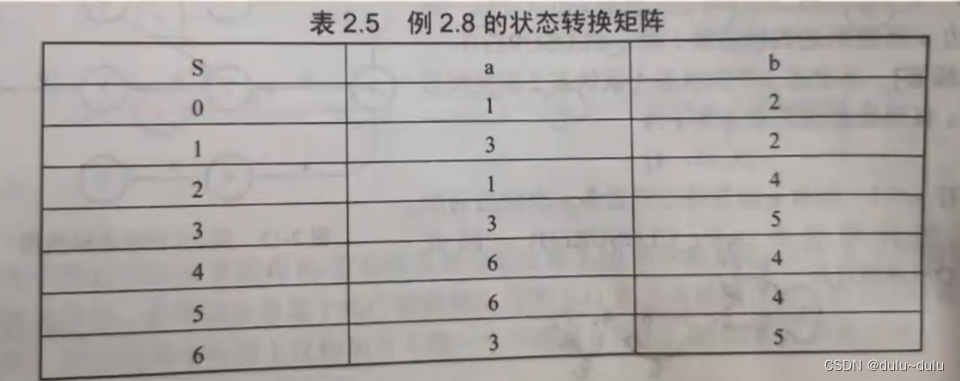
再根据状态转换矩阵可得图DFA

注:这个图怎么判断这个状态是不是一个终态(一个圈还是两个圈),那么我们只需要看状态转换表
表中含有Y的集合,就是终态,需要画两个圈

2.DFA的化简

这里终态和非终态的状态分别为终态={3,4,5,6},非终态={0,1,2}
对于非终态{0,1,2}:
将{0,1,2}分别输入a,即{0,1,2}a,通过状态转换矩阵可知,{0,1,2}a={1,3},{1,3}对于{0,1,2}而言,不是包含关系,所以
将得到1的状态和得到3的状态分开:
{0,2}-->{1},{1}--->{3}
再对{0,2}输入b的状态:
{0,2}b--->{2,4},{2,4}不包含在{0,2}中,所以{0}--->{2},{2}---->{4}

对于终态{3,4,5,6}:
{3,4,5,6}a={3,6},包含关系
{3,4,5,6}b={4,5},包含关系
对于非终态有{0}{1}{2}状态,对于终态有{3,4,5,6}状态,将他视为状态{3},那么

这里还是根据状态转换矩阵画,只是看到{3,4,5,6}都指向状态{3}

3.DFA和NFA的区别
NFA是不确定的有穷自动机,DFA是确定的有穷自动机
DFA与NFA的区别在于,NFA的状态转换过程中可以有空串,如下图即为NFA:
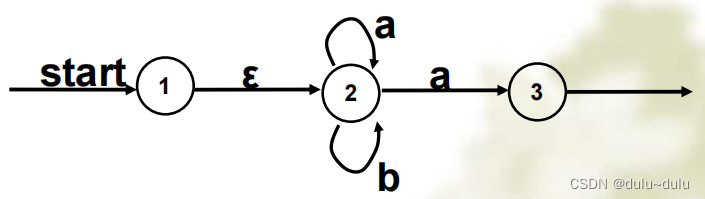 这就导致了一个问题:开始之后,在给出字符a或b之前,我们能够确定当前是处于1状态还是2状态吗?很显然,我们是无法确定的,因此才被称为不确定的有穷自动机,因为空串的存在,我们无法确定当前的具体状态是什么。
这就导致了一个问题:开始之后,在给出字符a或b之前,我们能够确定当前是处于1状态还是2状态吗?很显然,我们是无法确定的,因此才被称为不确定的有穷自动机,因为空串的存在,我们无法确定当前的具体状态是什么。
所以NFA的不确定表现我们可以概括为:1.多值映射 2.带空转移
所以我们要将NFA转换为DFA
