Stochastic Approximation 随机近似方法的详解之(三)Dvoretzky’s convergence theorem
定理内容
Theorem 6.2 (Dvoretzky’s Theorem). Consider a stochastic process
wk+1=(1−αk)wk+βkηkw_{k+1}=\left(1-\alpha_k\right) w_k+\beta_k \eta_kwk+1=(1−αk)wk+βkηk,
其中{αk}k=1∞,{βk}k=1∞,{ηk}k=1∞\{\alpha_k\}^\infty_{k=1},\{\beta_k\}^\infty_{k=1},\{\eta_k\}^\infty_{k=1}{αk}k=1∞,{βk}k=1∞,{ηk}k=1∞都是随机序列。这里αk≥0,βk≥0{\alpha_k} \ge 0,{\beta_k} \ge 0αk≥0,βk≥0 对于所有的kkk都是成立的。那么 wkw_{k}wk would converge to zero with probability 1 if the following conditions are satisfied:
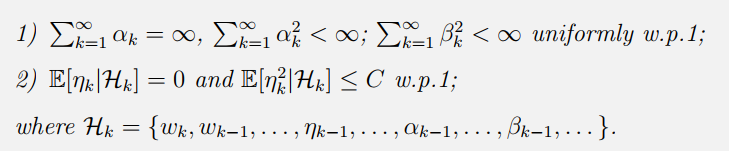
要点阐释
- RM算法里面的αk{\alpha_k}αk是确定性的。然而Dvoretzky’s Theorem中 αk,βk{\alpha_k},{\beta_k}αk,βk 可以是由Hk\mathcal H_kHk决定的随机变量。因此Dvoretzky’s Theorem 更加通用和强大。
- 对于uniformly w.p.1 的解释:

- 不再要求观测误差项ηk\eta_kηk的系数βk\beta_kβk的收敛速度了,收敛的快也没有关系。

证明在这里不展开,需要用到quasimartingales的知识

应用
证明Robbins-Monro theorem:
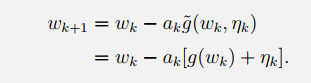
我们在等式两边同时减去目标根:
wk+1−w∗=wk−w∗−ak[g(wk)−g(w∗)+ηk]w_{k+1}-w^*=w_k-w^*-a_k\left[g\left(w_k\right)-g\left(w^*\right)+\eta_k\right]wk+1−w∗=wk−w∗−ak[g(wk)−g(w∗)+ηk]
然后就有:(注意,下面用到了中值定理)

注意这里的αk\alpha_kαk不再是确定的了,而是由wk和wk′w_k和w_k'wk和wk′共同决定的随机序列。对照Dvoretzky’s convergence theorem成立的条件,发现都满足:

到这里也就证明了RM算法求解方程根的收敛性。
定理的扩展:
原定理只能解决单变量的问题,不够使啊。必须扩展一下,让它可以处理多变量。扩展后的Dvoretzky’s convergence theorem 可以用来分析一些随机迭代算法的收敛性:比如Q-learning和TD算法。
扩展后的定理的内容:

在这样的定义下,原先数值上的大小比较就变成了不同向量之间的max norm的比较。注意哈,Hk\mathcal H_kHk是历史数据序列。
顺便解释一下max norm:

定理扩展的一些说明
- 扩展后的定理比原定理更加通用。首先,由于最大范数(the maximum norm)的引入,它可以处理多元变量的情况,对于具有很多个状态的强化学习问题,这一点很重要。第二,相比于原定理对E[ek(x)∣Hk]=0\mathbb{E}\left[e_k(x) \mid \mathcal{H}_k\right]=0E[ek(x)∣Hk]=0 and var[ek(x)∣Hk]≤C\operatorname{var}\left[e_k(x) \mid \mathcal{H}_k\right] \leq Cvar[ek(x)∣Hk]≤C的要求,this theorem only requires that the expectation and variance are bounded by the error ∆k。
- 虽然(6.9)只是针对单个状态,但它可以处理多个状态的原因是是因为条件3和4,它们是针对整个状态空间的。此外, 在应用该定理证明RL算法的收敛性时,我们需要表明(6.9)对每个状态都有效。
参考
https://github.com/MathFoundationRL/Book-Mathmatical-Foundation-of-Reinforcement-Learning
