线性代数(一)
1.标量:标量由只有⼀个元素的张量表⽰。
x = np.array(3.0)
y = np.array(2.0)
x + y, x * y, x / y, x ** y
(array(5.), array(6.), array(1.5), array(9.))
2.向量:向量可以被视为标量值组成的列表,列向量是向量的默认⽅向。
x = np.arange(4)
array([0., 1., 2., 3.])
在数学中,向量x可以写为:
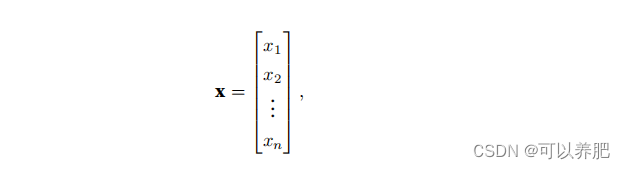
其中x1, . . . , xn是向量的元素。在代码中,我们通过张量的索引来访问任⼀元素。
x[3]
array(3.)
3. 矩阵:矩阵将向量从⼀阶推⼴到⼆阶。
A = np.arange(20).reshape(5, 4)
array([[ 0., 1., 2., 3.],[ 4., 5., 6., 7.],[ 8., 9., 10., 11.],[12., 13., 14., 15.],[16., 17., 18., 19.]])
对于任意A ∈ R m×n,A的形状是(m,n)或m × n。

当我们交换矩阵的⾏和列时,结果称为矩阵的转置(transpose)。
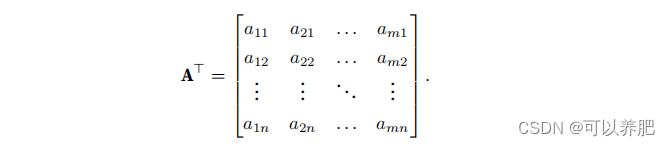
A.T
array([[ 0., 4., 8., 12., 16.],[ 1., 5., 9., 13., 17.],[ 2., 6., 10., 14., 18.],[ 3., 7., 11., 15., 19.]])
4.张量:有几个中括号就是几维张量。
X = np.arange(24).reshape(2, 3, 4)
array([[[ 0., 1., 2., 3.],[ 4., 5., 6., 7.],[ 8., 9., 10., 11.]],[[12., 13., 14., 15.],[16., 17., 18., 19.],[20., 21., 22., 23.]]])
5.范数:在线性代数中,向量范数是将向量映射到标量的函数f。
范数的的公式:

L1范数,它表⽰为向量元素的绝对值之和(此时P等于1):

L2范数,它表示为向量元素的平⽅和的平⽅根(此时P等于2):
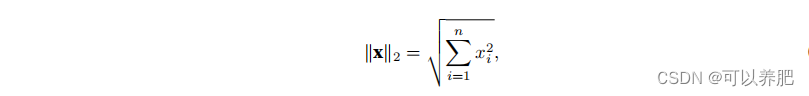
类似于向量的L2范数,矩阵X ∈ R m×n的Frobenius范数(Frobenius norm)是矩阵元素平⽅和的平⽅根: