二叉树的前序遍历
问题描述:
给你二叉树的根节点root,返回节点值的前序遍历。
示例 1:
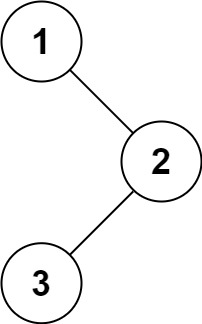
输入:root = [1,null,2,3] 输出:[1,2,3]
示例 2:
输入:root = [] 输出:[]
示例 3:
输入:root = [1] 输出:[1]
示例 4:

输入:root = [1,2] 输出:[1,2]
示例 5:
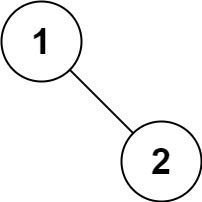
输入:root = [1,null,2] 输出:[1,2]
提示:
- 树中节点数目在范围
[0, 100]内 -100 <= Node.val <= 100
解题思路:
利用前序将遍历的数据放置到数组中,最后返回数组的地址即可
注意:
- 由于不知道二叉树中有多少个数据,不知道给数组扩容多少空间,这里就需要调用二叉树的节点个数的函数,最后要把数组的大小传出去输出。
- 对表示数组下标的i,每一层递归函数都有一个i,递归返回时下一层改变的i不会影响上一层中的i,故函数传参时需要传址
代码如下:
/** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*//*** Note: The returned array must be malloced, assume caller calls free().*/
int TreeSize(struct TreeNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
//将前序遍历之后的数据存入数组内
void _prevOrder(struct TreeNode* root, int* a, int* i)
{if (root == NULL)return;a[*i] = root->val;(*i)++;_prevOrder(root->left, a, &i);_prevOrder(root->right, a, &i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize)
{int size = TreeSize(root);int* a = (int*)malloc(size * sizeof(int));int i = 0;_prevOrder(root, a, &i);//将数组的大小传出去*returnSize = size;return a;
}小tip:已知二叉树的前序和中序得遍历过程,能否得到二叉树原本的结构?
假设前序为EFHIGJK,中序为HFIEJKG,试求出二叉树原本的结构。
通过之前的学习,我们可知前序遍历的顺序是根,左子树,右子树,中序遍历的顺序是左子树,根,右子树,由此可知,前序确定了该二叉树的根节点E,而中序可确定左子树和右子树,由此可知HFI为根节点的左子树,而JKG为根节点的右子树,又因为前序遍历完根节点之后就是左子树,故F为左子树,H为F的左子树,I为F的右子树,G为根节点的右子树,以此类推通过中序可发现,G后没遍历的数据,所以G无右子树,因为J比K先遍历,所以K不可能为J的左子树,因此只能为右子树。此二叉树的结构如下:
由此我们可以总结出一个结论:
已知前序+中序,后序+中序可推出二叉树结构,而后序+前序不可推。


