Stochastic Approximation 随机近似方法的详解之(一)
随机近似的定义:它指的是一大类随机迭代算法,用于求根或者优化问题。
Stochastic approximation refers to a broad class of stochastic iterative algorithms solving root finding or optimization problems.
temporal-difference algorithms是随机近似算法的一个特殊情景。
启发例子:均值估计
假设有限集合为X\mathcal{X}X,考虑随机变量XXX 是定义在这个集合的随机变量。我们的目的是估测 E[X]\mathbb{E}[X]E[X],我们是从样本中抽样的方法用样本均值x‾\overline{x}x 近似这个期望的值。x‾\overline{x}x 怎么来算呢?
抽取所有样本然后求均值的方法对于样本量巨大的情况显得很慢。
我们可以考虑用增量迭代(incremental and iterative)的方法:
先说结论,对一个新来的抽样样本,我们可以用这样的方法更新均值:

证明如下:
wk+1=1k∑i=1kxi=1k(∑i=1k−1xi+xk)=1k((k−1)wk+xk)=wk−1k(wk−xk)w_{k+1}=\frac{1}{k} \sum_{i=1}^k x_i=\frac{1}{k}\left(\sum_{i=1}^{k-1} x_i+x_k\right)=\frac{1}{k}\left((k-1) w_k+x_k\right)=w_k-\frac{1}{k}\left(w_k-x_k\right)wk+1=k1∑i=1kxi=k1(∑i=1k−1xi+xk)=k1((k−1)wk+xk)=wk−k1(wk−xk)
整个过程数学展开如下:
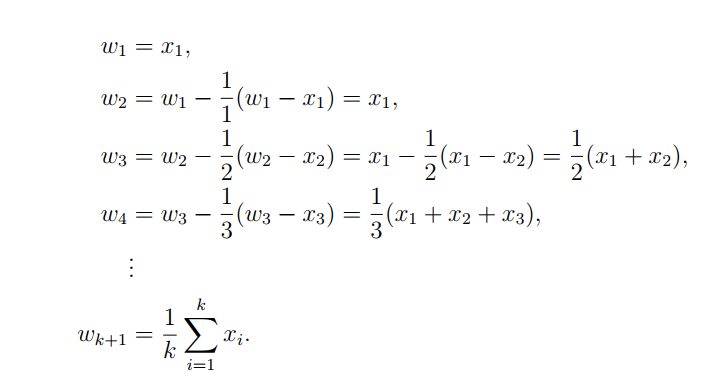
相比全部抽样完了再计算均值,这个方法的好处在于每到达一个样本就可以实时的更新均值,使用部分样本计算出来的样本均值可以立马使用。随着抽样的进行,均值的计算结果会越来越精确。
重点!!而上面的均值迭代更新公式可以更一般地表示为: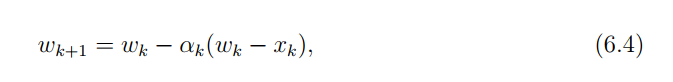
当这个系数αk\alpha_kαk满足一些条件的时候,这个更新公式是会收敛到 E[X]\mathbb{E}[X]E[X] 的。
至此,我们已经见识了(6-2)和(6-4)两种随机迭代算法。
