暴力递归到动态规划
暴力递归到动态规划
假设有排成一行的n个位置, 记为1~n,n-定大于或等于2。开始时机器人在其中的m位置上(m 一定是1~n中的一个)。如果机器人来到1位置,那么下一步只能往右来到2位置;如果机器人来到n位置, 那么下一步只能往左来到n-1位置;如果机器人来到中间位置,那么下一步可以往左走或者往右走;规定机器人必须走k步,最终能来到p位置(p也是1~n中的一个)的方法有多少种?给定四个参数n、m、k、p,返回方法数。
暴力递归
public static int robot(int n, int m, int k, int p){// 无效参数的情况if (n < 2 || m < 1 || m > n || k < 1 || p < 1 || p > n)return 0;return walk(n, m, k, p);
}// n 还是表示一共n个位置,p 还是表示目标位置
// cur 表示当前位置,rest表示还能走几步
private static int walk(int n, int cur, int rest, int p) {// 如果没有剩余步数了,当前的cur位置就是最后的位置// 如果最后的位置停在P上,那么之前做的移动是有效的// 如果最后的位置没在P上,那么之前做的移动是无效的if (rest == 0)return cur == p ? 1 : 0;if (cur == 1)return walk(n, cur + 1, rest - 1, p);if (cur == n)return walk(n, cur - 1, rest - 1, p);// 如果还有rest步要走,而当前的cur位置在中间位置上,那么当前这步可以走向左,也可以走右// 走向左之后,后续的过程就是,来到cur-1位置 上,还剩rest-1步要走// 走向右之后,后续的过程就是,来到cur+1位置. 上,还剩rest-1步要走// 走向左、走向右是截然不同的方法,所以总方法数要都算上return walk(n, cur - 1, rest - 1, p) + walk(n, cur + 1, rest - 1, p);
}
这种解法是最纯粹的暴力递归,有一些是重复计算。可以发现递归时只有两个参数对结果有实际影响
当前位置 剩余步数 ,如果将这两个参数的取值组成一张矩阵,计算好的数据存在矩阵中,当碰到有重复计算时只需要取值即可。
半动态规划
// 上述的这种暴力递归方法是有重复计算的。可以看出递归中n、p两个参数是固定不变的,结果只取决于(m,k)的组合,如果有
// 一个cache存放各种组合的结果,当重复计算时只需要从cache中返回结果。
public static int robotCache(int n, int m, int k, int p){// 无效参数的情况if (n < 2 || m < 1 || m > n || k < 1 || p < 1 || p > n)return 0;int[][] cache = new int[n + 1][k + 1];// 默认将cache所有元素都设为-1,表示从来没计算过,当递归访问某个元素时发现不是-1时说明已经计算过了,直接取值即可for (int[] ints : cache) Arrays.fill(ints, -1);return walkCache(n, m, k, p, cache);
}// 此时,所有的递归都要带上cache这张表一起玩
private static int walkCache(int n, int cur, int rest, int p, int[][] cache) {if (cache[cur][rest] != -1)return cache[cur][rest];if (rest == 0){cache[cur][rest] = cur == p ? 1 : 0;return cache[cur][rest];}if (cur == 1){cache[cur][rest] = walkCache(n, cur + 1, rest - 1, p, cache);return cache[cur][rest];}if (cur == n){cache[cur][rest] = walkCache(n, cur - 1, rest - 1, p, cache);return cache[cur][rest];}// 在中间位置cache[cur][rest] = walkCache(n, cur - 1, rest - 1, p, cache) +walkCache(n, cur + 1, rest - 1, p, cache);return cache[cur][rest];
}
通过分析发现,当cur=1cur=1cur=1 时,依赖 cache[cur+1][rest−1]cache[cur+1][rest-1]cache[cur+1][rest−1] 的值;当 cur=ncur=ncur=n 时,依赖 cache[cur−1][rest−1]cache[cur-1][rest-1]cache[cur−1][rest−1] 的值;当cur不在首尾时,依赖 cache[cur−1][rest−1]cache[cur-1][rest-1]cache[cur−1][rest−1] 和 cache[cur+1][rest−1]cache[cur+1][rest-1]cache[cur+1][rest−1] 。没有cur=0cur=0cur=0 的情况,虽然cache容量为(N+1)×(K+1)(N+1) \times (K+1)(N+1)×(K+1) ,但那是为了方便运算而已。初始情况下,rest=0rest=0rest=0,如果cur≠pcur \neq pcur=p 则为0,否则为1。假设目标位置p=3p=3p=3 如下图所示:
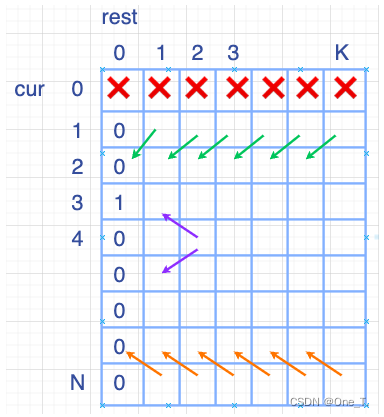
如果确定了这种依赖关系后,直接填表就好了,连递归都省了。
纯粹动态规划
public static int dp(int n, int m, int k, int p){// 无效参数的情况if (n < 2 || m < 1 || m > n || k < 1 || p < 1 || p > n)return 0;int[][] cache = new int[n + 1][k + 1];cache[p][0] = 1;// 先填列再填行for (int col = 1; col < cache[0].length; col++) {for (int row = 1; row < cache.length; row++) {if (row == 1)cache[row][col] = cache[row + 1][col - 1];else if (row == cache.length - 1)cache[row][col] = cache[row - 1][col - 1];elsecache[row][col] = cache[row - 1][col - 1] + cache[row + 1][col - 1];}}return cache[m][p];
}
