最长子序列问题(LCS)--动态规划解法
题目描述:
如果Z既是X的子序列,又是Y的子序列,则称Z为X和Y的公共子序列。
如果给定X、Y,求出Y及其长度。
示例:
输入
ABCPDSFJGODIHJOFDIUSHGD
OSDIHGKODGHBLKSJBHKAGHI输出
SDIHODSHG
9分析:
c[i][j]表示X从0到i与Y从0到j之间公共子序列的长度。
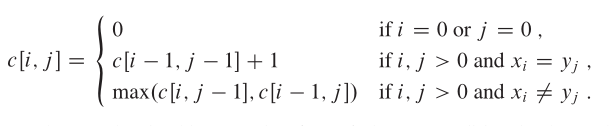
代码 :
//最长子序列问题,不是最长字串问题
#include<iostream>
#include<stack>
using namespace std;const int N = 1000;
int dp[N][N] = { 0 };
int path[N][N];
int main()
{string a, b;cin >> a;cin >> b;int lena = a.size();int lenb = b.size();for (int i = 0; i <lena-1; i++){for (int j = 0; j <lenb-1; j++){if (a[i] == b[j]){dp[i+1][j+1] = dp[i][j] + 1;path[i + 1][j + 1] = 1;}else if (dp[i][j + 1] >= dp[i + 1][j]){dp[i + 1][j + 1] = dp[i][j + 1];path[i + 1][j + 1] = 2;}else{dp[i + 1][j + 1] = dp[i+1][j];path[i + 1][j + 1] = 3;}}}cout << "dp数组为:" << endl;for (int i = 0; i < lena; i++){for (int j = 0; j < lenb; j++){cout << dp[i][j] << ' ';}cout << endl;}cout << "最长子序列数为:" << dp[lena - 1][lenb - 1] << endl;//存放最长子序列stack<char>same;for (int i = lena - 1, j = lenb - 1; i >= 0 && j >= 0;){if (path[i][j] == 1){i--;j--;same.push(a[i]);}else if (path[i][j] == 2){i--;}else{j--;}}cout << "最长子序列为";while (!same.empty()){cout << same.top();same.pop();}cout << endl;system("pause");return 0;}