当前位置：首页 > news >正文

【LeetCode】剑指 Offer 19. 正则表达式匹配 p124 -- Java Version

news 2025/8/21 8:01:19

题目链接：https://leetcode.cn/problems/zheng-ze-biao-da-shi-pi-pei-lcof/

1. 题目介绍（19. 正则表达式匹配）

请实现一个函数用来匹配包含'. '和'*'的正则表达式。模式中的字符'.'表示任意一个字符，而’*'表示它前面的字符可以出现任意次（含0次）。在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串"aaa"与模式"a.a"和"ab*ac*a"匹配，但与"aa.a"和"ab*a"均不匹配。

【测试用例】：
示例 1:

输入:
s = “aa”
p = “a”
输出: false
解释: “a” 无法匹配 “aa” 整个字符串。

示例 2:

输入:
s = “aa”
p = “a*”
输出: true
解释: 因为 ‘*’ 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 ‘a’。因此，字符串 “aa” 可被视为 ‘a’ 重复了一次。

示例 3:

输入:
s = “ab”
p = “."
输出: true
解释: ".” 表示可匹配零个或多个（‘*’）任意字符（‘.’）。

示例 4:

输入:
s = “aab”
p = “cab”
输出: true
解释: 因为 ‘*’ 表示零个或多个，这里 ‘c’ 为 0 个, ‘a’ 被重复一次。因此可以匹配字符串 “aab”。

示例 5:

输入:
s = “mississippi”
p = “misisp*.”
输出: false

【条件约束】：

提示

s 可能为空，且只包含从 a-z 的小写字母。
p 可能为空，且只包含从 a-z 的小写字母以及字符 . 和 *，无连续的 '*'。

【相似题目】：

【LeetCode】No.10. Regular Expression Matching – Java Version

2. 题解

2.1 递归 – O(2ⁿ)

时间复杂度O(2ⁿ)，空间复杂度O(n)

在这里插入图片描述

class Solution {public boolean isMatch(String s, String p) {if (p.isEmpty()) return s.isEmpty();int sx = 0;int px = 0;return matchCore(s.toCharArray(), sx, p.toCharArray(), px);}public boolean matchCore(char[] str, int sx, char[] pattern, int px) {// 递归终止条件// 1. 同时结束if (sx == str.length && px == pattern.length) {return true;}// 2. pattern先结束if (sx != str.length && px == pattern.length) {return false;}// 当模式中的第二个字符是'*'时if (px + 1 < pattern.length && pattern[px+1] == '*' ){// 且模式的当前字符与字符串中的字符相匹配 or 模式当前字符为'.'，可以匹配任意一个字符，if (sx != str.length && (pattern[px] == str[sx] || (pattern[px] == '.'))) {// 如果模式中的第一个字符和字符串中的第一个字符相匹配，下面就有2种选择// 1. 匹配1次或多次，一个一个往后匹配return matchCore(str, sx+1, pattern, px)// 2. 匹配0次,pattern直接跳过两个字符，即忽略"x*"|| matchCore(str, sx, pattern, px+2);} else // 匹配0次,pattern直接跳过两个字符，即忽略"x*"return matchCore(str, sx, pattern, px+2);} // 当模式中的字符是'.'时，或模式中字符不是'.'，但仍与字符串中字符相匹配时，接着匹配后面的字符if (sx != str.length && (str[sx] == pattern[px] || pattern[px] == '.'))return matchCore(str, sx+1, pattern, px+1);return false;}
}

在这里插入图片描述

2.2 动态规划 – O(mn)

时间复杂度O(mn)，空间复杂度O(mn)
不得不说，动态规划确实快。
在这里插入图片描述

思路图解：

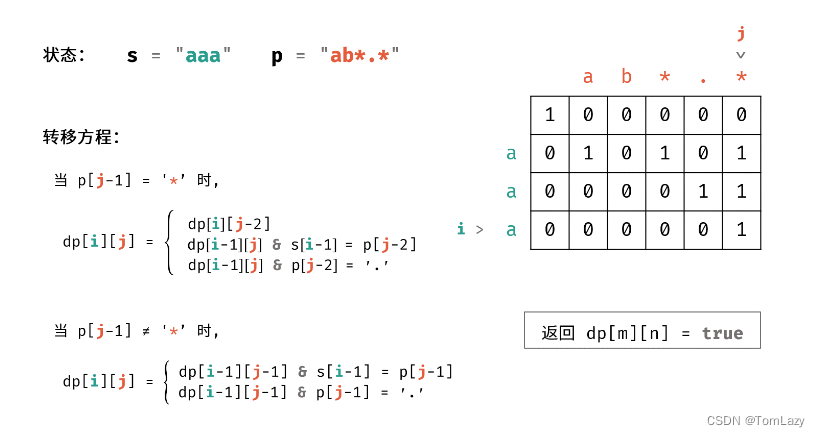
class Solution {public boolean isMatch(String s, String p) {int m = s.length() + 1, n = p.length() + 1;boolean[][] dp = new boolean[m][n];// dp[0][0] = true： 代表两个空字符串能够匹配。dp[0][0] = true;// 初始化首行// dp[0][j] = dp[0][j - 2] 且 p[j - 1] = '*'： 首行 s 为空字符串，因此当 p 的偶数位为 * 时才能够匹配（即让 p 的奇数位出现 0 次，保持 p 是空字符串）for(int j = 2; j < n; j += 2)dp[0][j] = dp[0][j - 2] && p.charAt(j - 1) == '*';// 状态转移for(int i = 1; i < m; i++) {for(int j = 1; j < n; j++) {dp[i][j] = p.charAt(j - 1) == '*' ?dp[i][j - 2] || dp[i - 1][j] && (s.charAt(i - 1) == p.charAt(j - 2) || p.charAt(j - 2) == '.') :dp[i - 1][j - 1] && (p.charAt(j - 1) == '.' || s.charAt(i - 1) == p.charAt(j - 1));}}return dp[m - 1][n - 1];}
}