数据结构 | 二叉树的各种遍历
数据结构 | 二叉树的各种遍历
文章目录
- 数据结构 | 二叉树的各种遍历
- 创建节点 && 创建树
- 二叉树的前中后序遍历
- 二叉树节点个数
- 二叉树叶子节点个数
- 二叉树第k层节点个数
- 二叉树查找值为x的节点
- 二叉树求树的高度
- 二叉树的层序遍历
- 判断二叉树是否是完全二叉树
我们本章来实现二叉树的这些功能
Tree.h
#pragma once#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef int BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;//创建节点
BTNode* BuyTreeNode(int x);
//创建树
BTNode* CreateTree();
// 二叉树销毁
void BinaryTreeDestory(BTNode* root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);
// 求树的高度
int TreeHeight(BTNode* root);
- 我们先来几个简单的
创建节点 && 创建树
- 直接手动个创建即可,很简单~~
//创建节点
BTNode* BuyTreeNode(int x)
{BTNode* root = (BTNode*)malloc(sizeof(BTNode));if (root == NULL){perror("malloc fail\n");exit(-1);}root->data = x;root->left = NULL;root->right = NULL;return root;
}
//创建树
BTNode* CreateTree()
{BTNode* node1 = BuyTreeNode(1);BTNode* node2 = BuyTreeNode(2);BTNode* node3 = BuyTreeNode(3);BTNode* node4 = BuyTreeNode(4);BTNode* node5 = BuyTreeNode(5);BTNode* node6 = BuyTreeNode(6);BTNode* node7 = BuyTreeNode(7);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;node5->right = node7;return node1;
}
二叉树的前中后序遍历
- 这里也是很简单,也可以看做下图这样遍历,或者画一下递归展开图
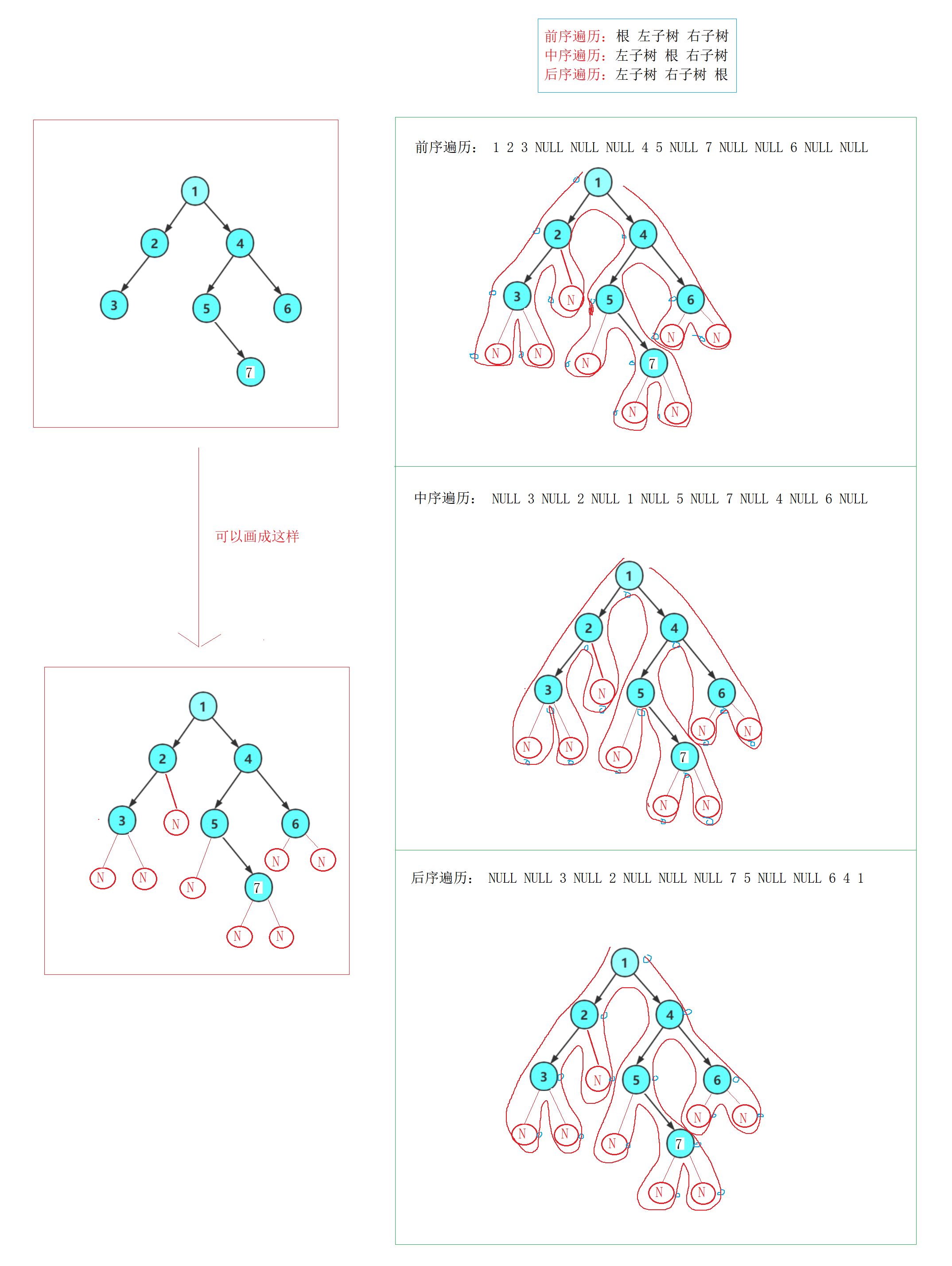
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%d ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);
}
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}BinaryTreeInOrder(root->left);printf("%d ", root->data);BinaryTreeInOrder(root->right);
}
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}BinaryTreePostOrder(root->left);BinaryTreePostOrder(root->right);printf("%d ", root->data);
}
二叉树节点个数
- 我们这里看一下递归展开图
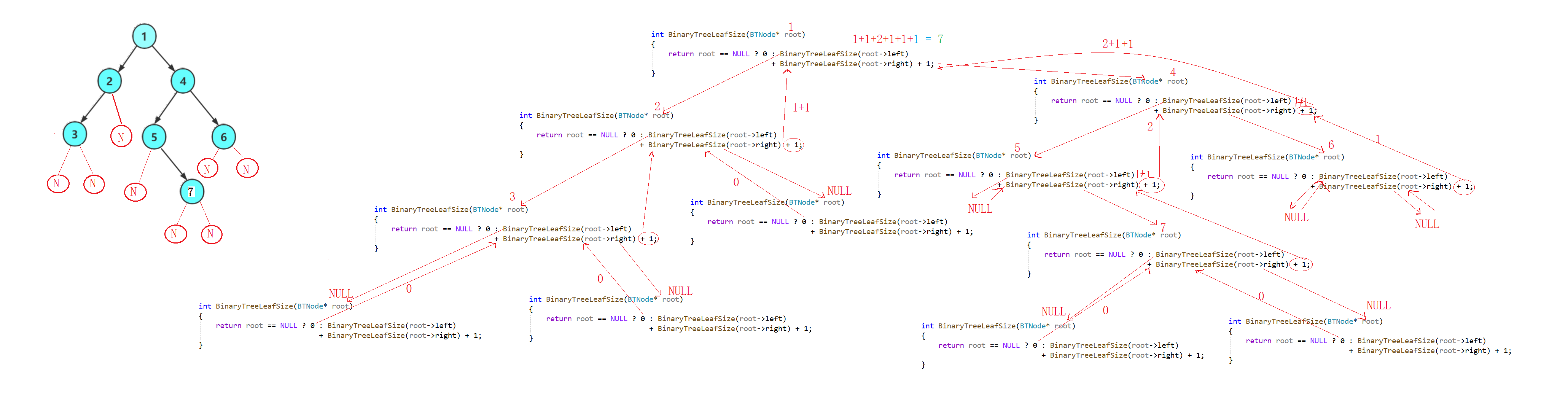
int BinaryTreeSize(BTNode* root)
{return root == NULL ? 0 : BinaryTreeSize(root->left)+ BinaryTreeSize(root->right);
}
二叉树叶子节点个数
- 为空就返回0
- 不是空,是叶子,返回1
- 不是空,也不是叶子,就递归左子树和右子树
int BinaryTreeLeafSize(BTNode* root)
{// 为空返回0if (root == NULL)return 0;//不是空,是叶子 返回1if (root->left == NULL && root->right == NULL)return 1;// 不是空 也不是叶子 分治=左右子树叶子之和return BinaryTreeLeafSize(root->left)+ BinaryTreeLeafSize(root->right);
}
二叉树第k层节点个数
- k是1的时候就是一层,就返回1
- 递归左子树加右子树,每次递归k-1
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL)return NULL;if (k == 1)return 1;//递归左子树加右子树,每次递归k-1return BinaryTreeLevelKSize(root->left, k - 1)+ BinaryTreeLevelKSize(root->right, k - 1);
}
二叉树查找值为x的节点
- 先看根节点是不是要找的
- 然后递归左子树和右子树
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;//根if (root->data == x)return root;//左子树BTNode* ret1 = BinaryTreeFind(root->left, x);if (ret1)return ret1;//右子树BTNode* ret2 = BinaryTreeFind(root->right, x);if (ret2)return ret2;return NULL;
}
二叉树求树的高度
- 遍历左子树和右子树(每次遍历都要保存值)
- 返回最高的那个子树然后加1(根)
int TreeHeight(BTNode* root)
{if (root == NULL)return NULL;//遍历左子树和右子树int left = TreeHeight(root->left);int right = TreeHeight(root->right);//返回最高的那个子树然后加1(根)return left > right ? left + 1 : right + 1;
}
二叉树的层序遍历
- 这里的这个层序遍历就需要用到我们之前学过的队列了~~
- 这里用法是入根(root),然后带孩子节点
void BinaryTreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);//先入根if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){//取队头的数据BTNode* front = QueueFront(&q);QueuePop(&q);//打印数据printf("%d ", front->data);//将左子树和右子树代入进队列if (front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);}printf("\n");QueueDestroy(&q);
}
- 那如果要一层一层的打印,代码改怎么改呢?
- 一层一层的带,一层一层的出
// 层序遍历(一层一层的打印)
void _BinaryTreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);//先入根if (root)QueuePush(&q, root);int leveSize = 1;while (!QueueEmpty(&q)){while (leveSize--){//取队头的数据BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->data);if (front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);}printf("\n");leveSize = QueueSize(&q);}QueueDestroy(&q);
}
判断二叉树是否是完全二叉树
- 和上面的代码基本一样,取数据如果遇到空就跳出
- 如果前面遇到空以后,后面还有非空就不是完全二叉树
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);//先入根if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){// 取队头的数据BTNode* front = QueueFront(&q);QueuePop(&q);//等于空了就跳出,然后检查后面还有节点没有if (front == NULL)break;// 将左子树和右子树代入进队列QueuePush(&q, front->left);QueuePush(&q, front->right);}// 前面遇到空以后,后面还有非空就不是完全二叉树while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);// 如果是不是空就 return false;if (front){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}
