LeetCode算法复杂度分析(时间复杂度空间复杂度)
文章目录
- 前言
- 时间复杂度
- 1.概述
- 2.大O记法
- 3.常见类型
- 空间复杂度
- 1.概述
- 2.常见类型
- 典型算法的复杂度分析
- 1.递归算法
- 2.哈希表
前言
我们知道,研究算法的最终目的就是如何花更少的时间,如何占用更少的内存去完成相同的需求。
时间复杂度
1.概述
我们要计算算法时间耗费情况,但我们并不能将时间占用和空间占用量化。所以我们得度量算法的执行时间,那么如何度量呢?
我们分析一个算法的运行时间,最重要的就是把核心操作的次数和输入规模关联起来。
2.大O记法
在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,进而分析T(n)随着n的变化情况并确定T(n)的量级。
算法的时间复杂度,就是算法的时间量度,记作:T(n)=O(f(n))。它表示随着问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐近时间复杂度,简称时间复杂度,其中f(n)是问题规模n的某个函数。
所以计算时间复杂度主要分两步:统计操作数量&判断渐进上界
常用技巧:
(1)用常数1取代运行时间中的所有加法常数;
(2)在修改后的运行次数中,只保留高阶项;
(3)如果最高阶项存在,且常数因子不为1,则去除与这个项相乘的常数;
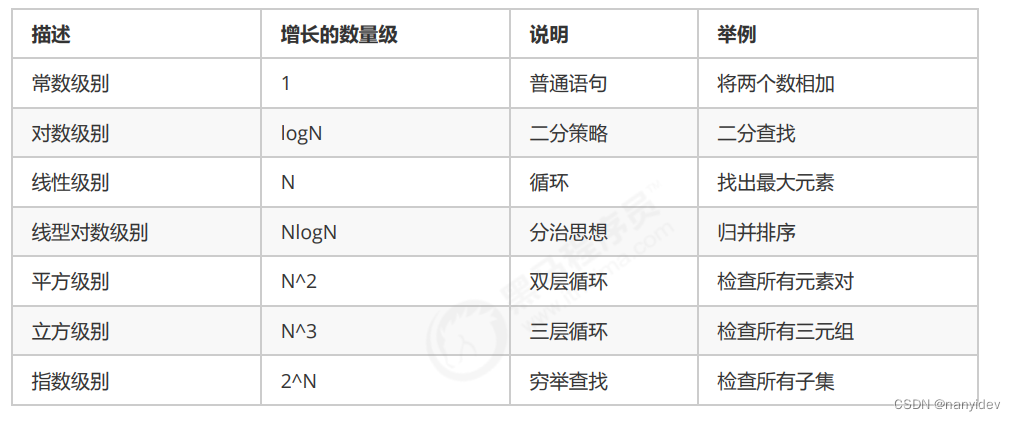
3.常见类型
首先,常见的时间复杂度类型排序:
O(1)<O(logn)<O(n)<O(nlogn)<O(n^2) <O(2^n) <O(n!)
空间复杂度
1.概述
统计 算法使用内存空间随着数据量变大时的增长趋势.
通常情况下,空间复杂度统计范围是「暂存空间」+「输出空间」
2.常见类型
同样是用大O来表示,只是这个是表示使用空间大小
O(1)<O(logn)<O(n)<O(n^2) <O(2^n)
典型算法的复杂度分析
1.递归算法
(1)时间复杂度
子问题个数乘以解决一个子问题需要的时间(即递归的次数 * 每次递归中的操作次数。)
例如,斐波那契数列
(2)空间复杂度
2.哈希表
空间换时间,查找的时间复杂度是O(1)
参考链接:https://www.helloalgo.com/chapter_computational_complexity/space_complexity/#232
https://programmercarl.com
