Homework 3: Higher-Order Functions, Self Reference, Recursion, Tree Recursion
Q1: Compose
编写一个高阶函数composer,它返回两个函数func和func_adder。 func是一个单参数函数,它应用到目前为止已经组合的所有函数。这些函数将首先应用最新的函数(参见doctests和示例)。 func_adder用于向我们的组合添加更多函数,当调用另一个函数g时,func_adder应该返回一个新的func和一个新的func_adder。
如果没有参数传入composer,则返回的func是恒等函数。
举例来说:
>>> add_one = lambda x: x + 1
>>> square = lambda x: x * x
>>> times_two = lambda x: x + x>>> f1, func_adder = composer()
>>> f1(1)
1>>> f2, func_adder = func_adder(add_one)
>>> f2(1)
2 # 1 + 1>>> f3, func_adder = func_adder(square)
>>> f3(3)
10 # 1 + (3**2)>>> f4, func_adder = func_adder(times_two)
>>> f4(3)
37 # 1 + ((2 * 3) **2)提示:你的
func_adder应该返回两个参数func和func_adder.我们知道什么函数返回
func和func_adder?(这个提示真的神来之笔:由于compose返回
func
func_adder这两个函数
所以func_adder应该是以新func为形参的compose函数
(func = lambda x:func(g(x))
g(x)作为原函数的参数x 逐级嵌套 )如图:
def composer(func=lambda x: x):"""Returns two functions -one holding the composed function so far, and anotherthat can create further composed problems.>>> add_one = lambda x: x + 1>>> mul_two = lambda x: x * 2>>> f, func_adder = composer()>>> f1, func_adder = func_adder(add_one)>>> f1(3)4>>> f2, func_adder = func_adder(mul_two)>>> f2(3) # should be 1 + (2*3) = 77>>> f3, func_adder = func_adder(add_one)>>> f3(3) # should be 1 + (2 * (3 + 1)) = 99"""def func_adder(g):"*** YOUR CODE HERE ***"return composer(lambda x:func(g(x)))return func, func_adderpass:
PS D:\pycharm\python document\CS61A class homework\hw03> python3 ok -q composer ===================================================================== Assignment: Homework 3 OK, version v1.18.1 =====================================================================~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ Running tests--------------------------------------------------------------------- Test summary1 test cases passed! No cases failed.
Q4: Count change
Once the machines take over, the denomination of every coin will be a power of two: 1-cent, 2-cent, 4-cent, 8-cent, 16-cent, etc. There will be no limit to how much a coin can be worth.
Given a positive integer total, a set of coins makes change for total if the sum of the values of the coins is total. For example, the following sets make change for 7:
- 7 1-cent coins
- 5 1-cent, 1 2-cent coins
- 3 1-cent, 2 2-cent coins
- 3 1-cent, 1 4-cent coins
- 1 1-cent, 3 2-cent coins
- 1 1-cent, 1 2-cent, 1 4-cent coins
Thus, there are 6 ways to make change for 7. Write a recursive function count_change that takes a positive integer total and returns the number of ways to make change for total using these coins of the future.
Hint: Refer the implementation of
count_partitionsfor an example of how to count the ways to sum up to a total with smaller parts. If you need to keep track of more than one value across recursive calls, consider writing a helper function.
分析:作者把此题核心分为两个函数
divide函数:
作用:
求 对于total 满足1------小于total的最大2的倍数 面值美分 的排列种类
核心:
将一种情况分为两种情况即:
当前有最大数的排列数量 和 无当前最大数的数量
举个例子如图(函数实现过程):

max1:
求的是 小于total的最大2的倍数
def divide(total,num):if num==1:return 1if total<num:return divide(total,num/2)return divide(total-num,num)+divide(total,num/2)def max1(total):if total<=1:return 1if total>0:return max1(total//2)*2
def count_change(total):"""Return the number of ways to make change for total.>>> count_change(7)6>>> count_change(10)14>>> count_change(20)60>>> count_change(100)9828>>> from construct_check import check>>> # ban iteration>>> check(HW_SOURCE_FILE, 'count_change', ['While', 'For'])True""""*** YOUR CODE HERE ***"if total==1:return 1return divide(total,max1(total))
pass结果:
PS D:\pycharm\python document\CS61A class homework\hw03> python3 ok -q count_change
=====================================================================
Assignment: Homework 3
OK, version v1.18.1
=====================================================================~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Running tests---------------------------------------------------------------------
Test summary1 test cases passed! No cases failed.
Q5: Towers of Hanoi
一个经典的难题称为塔的河内是一个游戏,包括三个 杆和许多不同尺寸的圆盘,圆盘可以在任何杆上滑动。 这个谜题从n磁盘开始,磁盘按照大小的升序整齐地堆叠在一起, start棒,顶部最小,形成圆锥形。
拼图的目的是将整个堆叠移动到end杆, 遵守以下规则:
- 一次只能移动一个磁盘。
- 每次移动包括从其中一根杆上取下顶部(最小)的圆盘, 把它滑到另一个杆上,在其他可能已经被 存在于该杆上。
- 不能将磁盘放在较小磁盘的顶部。
完成move_stack的定义,它将打印出执行以下操作所需的步骤: 将n盘从start棒移动到end棒,不违反 规则提供的print_move函数将打印出移动 从给定的origin到给定的destination的单个磁盘。
提示:在一张纸上画出几个带有各种
n的游戏,并尝试 找到一个适用于任何n的磁盘运动模式。在你的解决方案中, 当你需要移动任何数量的 小于n的圆盘从一个棒到另一个棒。如果你需要更多帮助, 以下提示。
分析:
核心:拆分思想(动态规划dp)
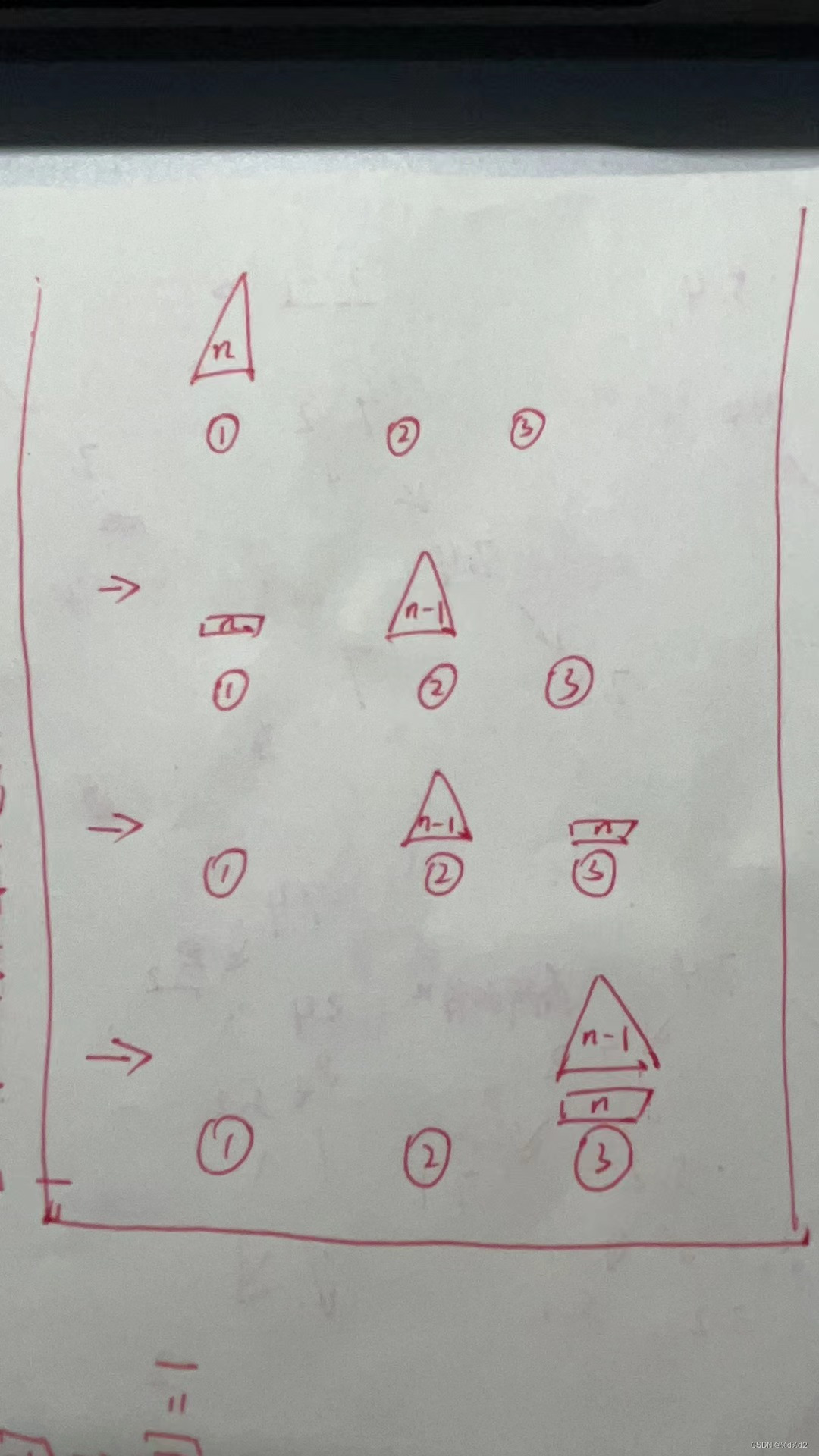
对于n个盘子需要从起点到终点的问题可以转化为
1.将n个盘子需要从起点到非起点或终点,
2.第n个盘子从起点到终点,
3.再将n-1盘子放到终点的过程
(1)其中对于n==2的情况(即递归终点)需要模拟出相应过程
注意:n==1需要额外说明
如图所示:
def print_move(origin, destination):"""Print instructions to move a disk."""print("Move the top disk from rod", origin, "to rod", destination)def move_stack(n, start, end):"""Print the moves required to move n disks on the start pole to the endpole without violating the rules of Towers of Hanoi.n -- number of disksstart -- a pole position, either 1, 2, or 3end -- a pole position, either 1, 2, or 3There are exactly three poles, and start and end must be different. Assumethat the start pole has at least n disks of increasing size, and the endpole is either empty or has a top disk larger than the top n start disks.>>> move_stack(1, 1, 3)Move the top disk from rod 1 to rod 3>>> move_stack(2, 1, 3)Move the top disk from rod 1 to rod 2Move the top disk from rod 1 to rod 3Move the top disk from rod 2 to rod 3>>> move_stack(3, 1, 3)Move the top disk from rod 1 to rod 3Move the top disk from rod 1 to rod 2Move the top disk from rod 3 to rod 2Move the top disk from rod 1 to rod 3Move the top disk from rod 2 to rod 1Move the top disk from rod 2 to rod 3Move the top disk from rod 1 to rod 3"""assert 1 <= start <= 3 and 1 <= end <= 3 and start != end, "Bad start/end""*** YOUR CODE HERE ***"n_s=0if 1!=start and 1!=end:n_s=1if 2!=start and 2!=end:n_s=2if 3!=start and 3!=end:n_s=3if n==1:print_move(start,end)returnif n==2:print_move(start,n_s)print_move(start,end)print_move(n_s,end)returnmove_stack(n-1,start,n_s)print_move(start,end)move_stack(n-1,n_s,end)
pass情况:
PS D:\pycharm\python document\CS61A class homework\hw03> python3 ok -q move_stack
=====================================================================
Assignment: Homework 3
OK, version v1.18.1
=====================================================================~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Running tests---------------------------------------------------------------------
Test summary1 test cases passed! No cases failed.

