【每日一题】从二叉搜索树到更大和树
文章目录
- Tag
- 题目来源
- 题目解读
- 解题思路
- 方法一:中序遍历的反序
- 方法二:后缀数组
- 写在最后
Tag
【中序遍历】【二叉树】【2023-12-04】
题目来源
1038. 从二叉搜索树到更大和树
题目解读
在二叉搜索树中,将每一个节点的值替换成树中大于等于该节点值的所有节点值之和。
解题思路
方法一:中序遍历的反序
前言
给的是一棵二叉搜索树(英文名称为 Binary Search Tree,以下简称为 BST),我们要充分利用 BST 的性质来解题。BST 的约束条件为:
- 节点的左子树的节点值都小于该节点的值;
- 节点的右子树的节点值都大于该节点的值;
- 左右子树也都是 BST。
根据 BST 的约束条件可以得到一条重要的性质:如果对 BST 进行中序遍历,那么将会得到 BST 中节点值升序的一个序列。
思路
我们以示例 1 为例来说明我们是如何利用 BST 的性质来解决本题的。
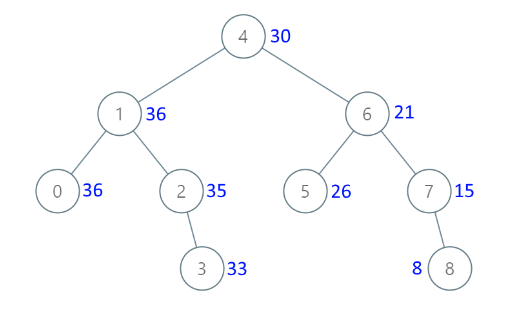
比如,为了计算根节点修改后的值,应该先遍历右子树的所有节点,因为 BST 的右子树的节点值都大于根节点的值,得有所有右子树的节点值之后,再加上根节点的值,即
8 + 7 + 6 + 5 + 4 = 30 8+7+6+5+4=30 8+7+6+5+4=30
这便是根节点修改后的值。我们在计算某个节点(后文称之为 “计算节点”)的大于等于该节点的所有节点之和是利用递归来实现的。
“递”:一直 “递” 到叶子节点,也就是到达了递归边界。
“归”:在归的过程中自底向上的将叶子节点到 “计算节点” 这一路上的所有节点值都修改了,修改为递归上来的 s(当前节点的右子树的所有节点之和)加上当前节点的值。
在更新了 “计算节点” 的值之后,递归修改 “计算节点” 的左子树。
算法
初始化全局变量 s = 0,从根节点开始递归修改,递归函数为:
- 递归出口为当前节点到达了叶子节点即
node == nullptr; - 递归修改右子树;
- 把当前节点的值加到
s中,接着修改当前节点的值; - 递归修改左子树。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
private: int s = 0;void dfs(TreeNode* node) {if (node == nullptr) {return;}dfs(node->right);s += node->val;node->val = s;dfs(node->left);}public:TreeNode* bstToGst(TreeNode* root) {dfs(root);return root;}
};
复杂度分析
时间复杂度: O ( n ) O(n) O(n), n n n 为 BST 的节点个数。
空间复杂度: O ( n ) O(n) O(n),最坏情况下,BST 退化成一条链,此时递归需要的栈空间为 O ( n ) O(n) O(n)。
方法二:后缀数组
熟悉 “如果对 BST 进行中序遍历,那么将会得到 BST 中节点值升序的一个序列” 这条性质的读者还可以有另一种解题思路。
首先将 BST 按中序遍历的顺序输出到数组中,得到升序数组 nums。数组中的数加上其后的所有数之和就是 BST 中的 “大于等于该节点值的所有节点值之和”。
于是需要维护一个后缀数组,最后将更新好的后缀数组中的值还原到二叉搜索树上。
该方法实现起来有些繁琐,感兴趣的读者可以自行实现。
写在最后
如果文章内容有任何错误或者您对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度方法,欢迎评论区交流。
最后,感谢您的阅读,如果感到有所收获的话可以给博主点一个 👍 哦。
