C++笔试训练day_1
文章目录
- 选择题
- 编程题
选择题

编程题

#include <iostream>
#include <algorithm>
#include <vector>using namespace std;int main() {int n = 0;cin >> n;vector<int> v;v.resize(3 * n);int x = 0;for(int i = 0; i < v.size(); i++){cin >> v[i];}sort(v.begin(), v.end());//int sum = 0;long long sum = 0;for(int j = 0; j < n; j++){sum += v[v.size() - (j + 1) * 2];}cout << sum << endl;return 0;
}
// 64 位输出请用 printf("%lld")
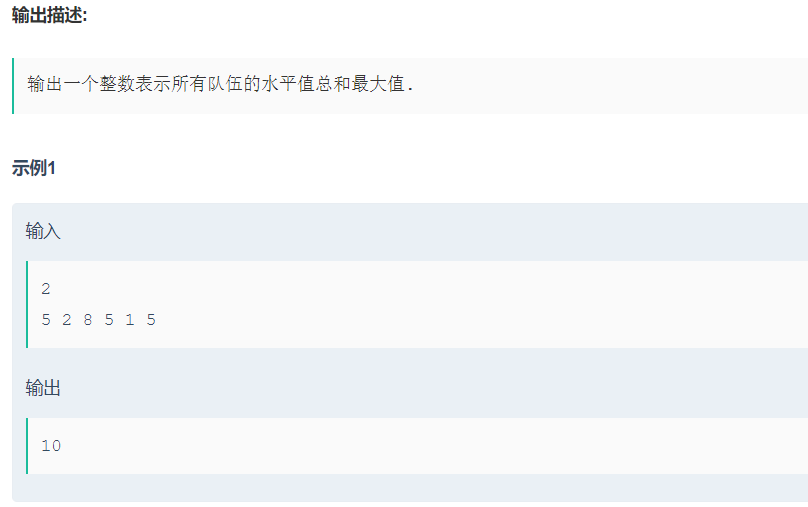
在本题中最重要的就是怎么进行分组,然后怎么取到每组里面的中位数:我们选择通过resize扩容vector然后输入数据,去对这组数据进行排序,而分组方式是第一组取一个最小值和最大的两个值,第二组取次小值和次大的两个值,一次类推,这样就保证了我们一定可以去取到次大的值。

因此中位数就是和6,结果sum就是9
而在已经排好序的vector中怎么直接去取到这两组中的中位数呢?
此时就要借助一个公式:**v.size() - 2 * (i + 1)**其中i表示第几组
第0组也就是第1组:中位数下标为6 - 2 = 4
第1组也就是第2组:中位数下标为6 - 4 = 2
其实这个公式也就是从后向前依次取倒数第2个值,size - 2,size - 4就是倒数第二个值和倒数第4个值,注意size值比下标多1
2.

#include <iostream>
using namespace std;int main() {string str1, str2;getline(cin, str1);getline(cin, str2);int hash[256] = {0};for(int i = 0; i < str2.size(); i++){hash[str2[i]]++;}string s;for(int j = 0; j < str1.size(); j++){if(hash[str1[j]] == 0){s += str1[j];}}cout << s << endl;return 0;
}
// 64 位输出请用 printf("%lld")
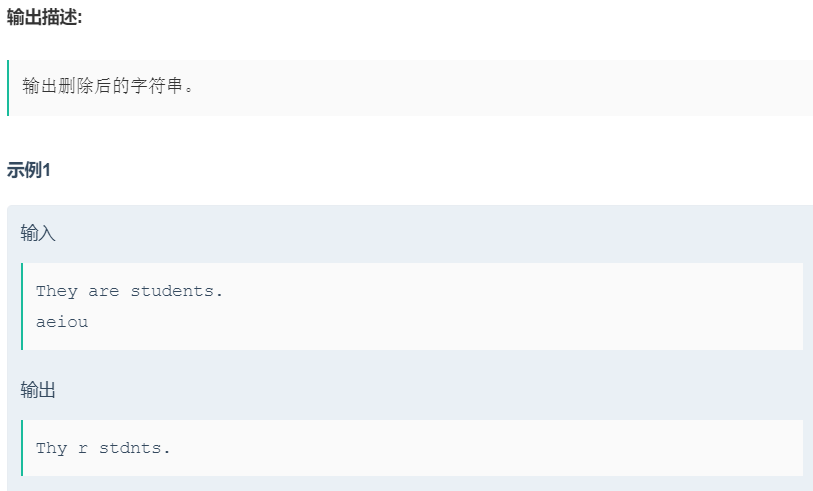
解题思路:利用哈希映射的特性来解决上述问题,就可以以O(n)的复杂度解决问题,先把不能出现的字符映射到hash表上,在对str1进行遍历,如果它在hash上对应的字符为0,就证明这个字符能出现。注意本题使用getline输入一行字符串
