算法练习-排序(一)
算法练习-排序(一)
文章目录
- 算法练习-排序(一)
- 1 排序算法
- 1.1 冒泡排序
- 1.1.1代码
- 1.2插入排序
- 1.2.1代码
- 1.3 选择排序
- 1.3.1代码
- 1.4归并排序
- 1.4.1代码
- 1.5 快速排序
- 1.5.1 思路
- 1.5.2 代码
- 2 题目
- 2.1 特殊排序
- 2.1.1 题目
- 2.1.2 题解
- 2.2 数组中的第k个最大元素
- 2.2.1 题目
- 2.2.2 题解
- 2.3 对链表进行插入排序
- 2.3.1 题目
- 2.3.2 题解
- 2.4 排序预处理
- 2.4.1 题目
1 排序算法
1.1 冒泡排序
1.1.1代码
void bubbleSort(int[] a, int n) {if (n <= 1) return;for (int i = 0; i < n; i++) { // 第几趟冒泡boolean flag = false;for (int j = 0; j < n - i - 1; j++) {if (a[j] > a[j + 1]) {int tmp = a[j];a[j] = a[j + 1];a[j + 1] = tmp;flag = true; // 表示有数据交换}}if (!flag) break;}
}
1.2插入排序
1.2.1代码
public static void InsertSort(int[] a, int n) {if (n <= 1) return;for (int i = 1; i < n; i++) {int value = a[i];for (int j = i - 1; j >= 0; --j) {if (a[j] > value) {a[j + 1] = a[j];} else {break;}}a[j + 1] = value;}
}1.3 选择排序
1.3.1代码
public void selectionSort(int[] a, int n) {if (n <= 1) return;for (int i = 0; i < n - 1; i++) {int minPos = i;for (int j = i; j < n; j++) {if (a[j] < a[minPos]) {minPos = j;}}int tmp = a[i];a[i] = a[minPos];a[minPos] = tmp;}
}
1.4归并排序
1.4.1代码
public void mergeSort(int[] a, int n) {mergeSort_r(a, 0, n - 1);
}private void mergeSort_r(int[] a, int p, int r) {if (p >= r) return;int q = p + (r - q) / 2;mergeSort_r(a, p, q);mergeSort_r(a, q + 1, r);merge(a, p, q, r);
}private void merge(int[] a, int p, int q, int r) {int i = p;int j = q + 1;int k = 0;int[] tmp = new int[r - q + 1];while (i <= q && j <= r) {if (a[i] <= a[j]) {tmp[k++] = a[i++];} else {tmp[k++] = a[j++];}}while (i <= q) {tmp[k++] = a[i++];}while (j <= r) {tmp[k++] = a[j++];}for (int i = 0; i < r - p; i++) {a[p + i] = tmp[i];}
}
1.5 快速排序
1.5.1 思路
先把数组中的一个数当作基准数,一般把数组最左面的数当作基准数,然后从两边进行检索。
先从右边检索比基准数小的,再从左边检索比基准数大的。
如果检索到了,就停下,交换这两个元素,然后继续检索
两个指针一旦相遇就停止检索,将基准数和相遇位置进行交换
1.5.2 代码
public static void quickSort(int[] a, int n) {quickSort_r(a, 0, n - 1);
}private void swap(int[] nums, int i ,int j) {int tmp = nums[i];nums[i] = nums[j];nums[j] = tmp;
}public static void quickSort_r(int[] arr, int left, int right) {if (left >= right) return;// 定义变量保存基准数int base = arr[left];// 定义变量i,指向最左边int i = left;// 定义变量j,指向最右边int j = right;// 当i和j不相遇时,在循环中进行检索while (i != j) {// 现由j从右往左检索while (arr[j] >= base && i < j) j--;while (arr[i] <= base && i < j) i++;// i 和 j都停下了,交换 i 和 j 位置的元素swap(arr, i, j);}swap(arr, left, i);quickSort_r(arr, left, i - 1);quickSort_r(arr, j + 1, right);}
public static void quickSort(int[] a, int n) {quickSort_r(a, 0, n - 1);
}private static void quickSort_r(int[] a, int p, int r) {if (p >= r) return;int q = partition(a, p, r);quickSort_r(a, p, q - 1);quickSort_r(a, q + 1, r);
}private static int partition(int[] a, int p, int r) {int i = p - 1; // [p, i]表示小于pivot值的元素for (int j = p; j < r; j++) {if (a[j] < a[r]) {swap(a, i + 1, j);i++;}}swap(a, i + 1, r);return i + 1;
}private void swap(int[] nums, int i, int j) {int tmp = nums[i];nums[i] = nums[j];nums[j] = tmp;
}
2 题目
2.1 特殊排序
2.1.1 题目
输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有奇数位于数组的前半部分,所有偶数位于数组的后半部分
2.1.2 题解
class Solution {public int[] exchange(int[] nums) {int i = 0;int j = nums.length - 1;while (i < j) {if (nums[i] % 2 == 1) {i++;continue;}if (nums[j] % 2 == 0) {j--;continue;}int tmp = nums[j];nums[i] = nums[j];nums[j] = tmp;i++;j--;}return nums;}
}
2.2 数组中的第k个最大元素
链接:https://leetcode.cn/problems/kth-largest-element-in-an-array
2.2.1 题目
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入: [3,2,1,5,6,4], k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4
2.2.2 题解
class Solution {public int findKthLargest(int[] nums, int k) {if (nums.length < k) return -1;return quickSort(nums, 0, nums.length - 1, k);}private int quickSort(int[] nums, int p, int r, int k) {if (p > r) return -1;int q = partition(nums, p ,r);if (q - p + 1 == k) {return nums[q];} else if (q - p + 1 < k) {return quickSort(nums, q + 1, r, k - (q - p + 1));} else {return quickSort(nums, p, q - 1, k);}}private int partition(int[] nums, int p, int r) {int i = p;int j = r - 1;while (i < j) {while (i < j && nums[i] > nums[r]) {i++;}while (i < j && nums[j] <= nums[r]) {j--;}if (i < j) {swap(nums, i, j);i++;j--;}}if (j >= p && nums[j] < nums[r]) {swap(nums, j , r);return j;} else {swap(nums, j + 1, r);return j + 1;}}private void swap(int[] arr, int i, int j) {int tmp = arr[i];arr[i] = arr[j];arr[j] = tmp;}
}
class Solution {public int findKthLargest(int[] nums, int k) {if (nums.length < k) return -1;return quickSort(nums, 0, nums.length - 1, k);}private int quickSort(int[] nums, int p, int r, int k) {if (p > r) return -1;int q = partition(nums, p ,r);if (q - p + 1 == k) {return nums[q];} else if (q - p + 1 < k) {return quickSort(nums, q + 1, r, k - (q - p + 1));} else {return quickSort(nums, p, q - 1, k);}}private int partition(int[] nums, int p, int r) {int i = p - 1; // [p, i]表示小于pivot值的元素for (int j = p; j < r; j++) {if (nums[j] > nums[r]) {swap(nums, i + 1, j);i++;}}swap(nums, i + 1, r);return i + 1;}private void swap(int[] arr, int i, int j) {int tmp = arr[i];arr[i] = arr[j];arr[j] = tmp;}
}
2.3 对链表进行插入排序
链接:https://leetcode.cn/problems/insertion-sort-list
2.3.1 题目
给定单个链表的头 head ,使用 插入排序 对链表进行排序,并返回 排序后链表的头 。
插入排序 算法的步骤:
插入排序是迭代的,每次只移动一个元素,直到所有元素可以形成一个有序的输出列表。
每次迭代中,插入排序只从输入数据中移除一个待排序的元素,找到它在序列中适当的位置,并将其插入。
重复直到所有输入数据插入完为止。
下面是插入排序算法的一个图形示例。部分排序的列表(黑色)最初只包含列表中的第一个元素。每次迭代时,从输入数据中删除一个元素(红色),并就地插入已排序的列表中。
对链表进行插入排序。
示例 1:
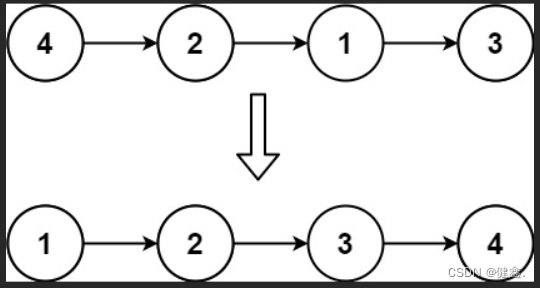
输入: head = [4,2,1,3]
输出: [1,2,3,4]
示例 2:

输入: head = [-1,5,3,4,0]
输出: [-1,0,3,4,5]
2.3.2 题解
class Solution {public ListNode insertionSortList(ListNode head) {if (head == null) return null;// 存储已经排序好的节点ListNode newHead = new ListNode(Integer.MIN_VALUE, null);// 遍历节点ListNode p = head;while (p != null) {ListNode tmp = p.next;// 寻找p节点插入的位置,插入到哪个节点后面ListNode q = newHead;while (q.next != null && q.next.val <= p.val) {q = q.next;}p.next = q.next;q.next = p;p = tmp;}return newHead.next;}
}
2.4 排序预处理
2.4.1 题目
有一组无序数据,找到出现次数最多的数据
public int maxCount(int[] data) {Arrays.sort(data);int n = data.length;int pre = -1;int count = 0;int max = -1;for (int i = 0; i < n; ++i) {if (data[i] == pre) {count++;if (max < count) max = count;} else {count = 1;pre = data[i];if (max < count) max = count;}}return max;
}
