Programming Contest 2023(AtCoder Beginner Contest 331)D题 Tile Pattern --- 题解
目录
D - Tile Pattern
题目大意:
思路:
代码:
D - Tile Pattern
D - Tile Pattern (atcoder.jp)
题目大意:
给你一个n和q,n为局部棋盘大小(n*n) 并且给出局部棋盘中黑白子位置的放置情况,q为查询次数,然后使用局部棋盘填充整个棋盘,全局棋盘大小为(10^9 * 10^9),然后一次查询会给出a b c d,(a,b)表示选中棋盘的左上角,(c,d)表示选中棋盘的右上角,然后问在这个选中区域中有多少个黑色棋子。
思路:
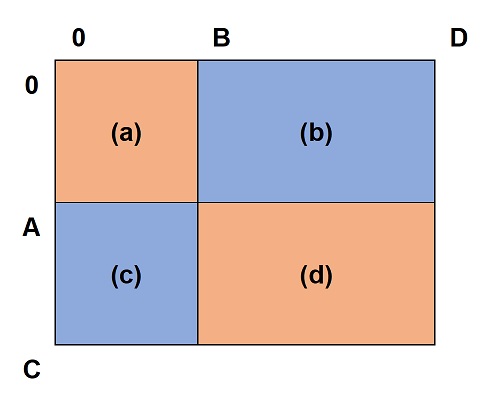
我们其实可以通过预处理这个局部棋盘矩阵,得到任意以(0,0)为左上角的矩阵的含有黑色棋子的个数,即dp[i][j]表示 (0,0) -> (i,j)的矩阵含有黑色棋子的个数。
如果把这个选中矩阵填充成 (0,0) -> (c,d). 那么答案就为 dp[c][d] - dp[c][b-1] - dp[a-1][d] + dp[a-1][b-1].
但是如果a b c d 都大于n,那么其实我们可以沿着这个思路,将d区看作是完整的m*n个局部棋盘,c区看作是列不全的m个局部棋盘,b区看作是行不全的n个局部棋盘,a区看作是列不全和行不全的棋盘,然后d区可以直接通过 m*m*dp[n][n]求得,c区和b区都分别等于m个列不全和行不全的局部棋盘和n个列不全和行不全的局部棋盘,然后这些局部棋盘又可以通过 dp[c][d] - dp[c][b-1] - dp[a-1][d] + dp[a-1][b-1]得到。
代码:
import java.io.*;
import java.math.BigInteger;
import java.util.StringTokenizer;/*** @ProjectName: study3* @FileName: Ex37* @author:HWJ* @Data: 2023/12/2 20:50*/
public class Ex37 {static long[][] dp;static int n;public static void main(String[] args) {n = input.nextInt();int q = input.nextInt();long[][] map = new long[n][n];dp = new long[n + 1][n + 1];for (int i = 0; i < n; i++) {String str = input.next();char[] s = str.toCharArray();for (int j = 0; j < n; j++) {if (s[j] == 'B') {map[i][j] = 1;}}}for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + map[i - 1][j - 1];}}for (int i = 0; i < q; i++) {int a = input.nextInt();int b = input.nextInt();int c = input.nextInt();int d = input.nextInt();long ans = f(a, b, c+1, d+1);out.println(ans);}out.flush();out.close();}public static long f(int a, int b, int c, int d){return g(c,d) - g(c,b) - g(a,d) + g(a,b);}public static long g(int a, int b){if (a <= n && b <= n) return dp[a][b];int Hq = a / n, Hr = a % n;int Wq = b / n, Wr = b % n;long ret = 0;ret += g(n, n) * Hq * Wq;ret += g(Hr, n) * Wq;ret += g(n, Wr) * Hq;ret += g(Hr, Wr);return ret;}static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));static Input input = new Input(System.in);static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static class Input {public BufferedReader reader;public StringTokenizer tokenizer;public Input(InputStream stream) {reader = new BufferedReader(new InputStreamReader(stream), 32768);tokenizer = null;}public String next() {while (tokenizer == null || !tokenizer.hasMoreTokens()) {try {tokenizer = new StringTokenizer(reader.readLine());} catch (IOException e) {throw new RuntimeException(e);}}return tokenizer.nextToken();}public String nextLine() {String str = null;try {str = reader.readLine();} catch (IOException e) {// TODO 自动生成的 catch 块e.printStackTrace();}return str;}public int nextInt() {return Integer.parseInt(next());}public long nextLong() {return Long.parseLong(next());}public Double nextDouble() {return Double.parseDouble(next());}public BigInteger nextBigInteger() {return new BigInteger(next());}}
}
/*
10 1
BBBWWWBBBW
WWWWWBBBWB
BBBWBBWBBB
BBBWWBWWWW
WWWWBWBWBW
WBBWBWBBBB
WWBBBWWBWB
WBWBWWBBBB
WBWBWBBWWW
WWWBWWBWWB
5 21 21 93*/
