当前位置： 首页 > news >正文

索莫菲模型的一些理解 Smomerfeld Model

news 2025/8/23 4:41:46

 

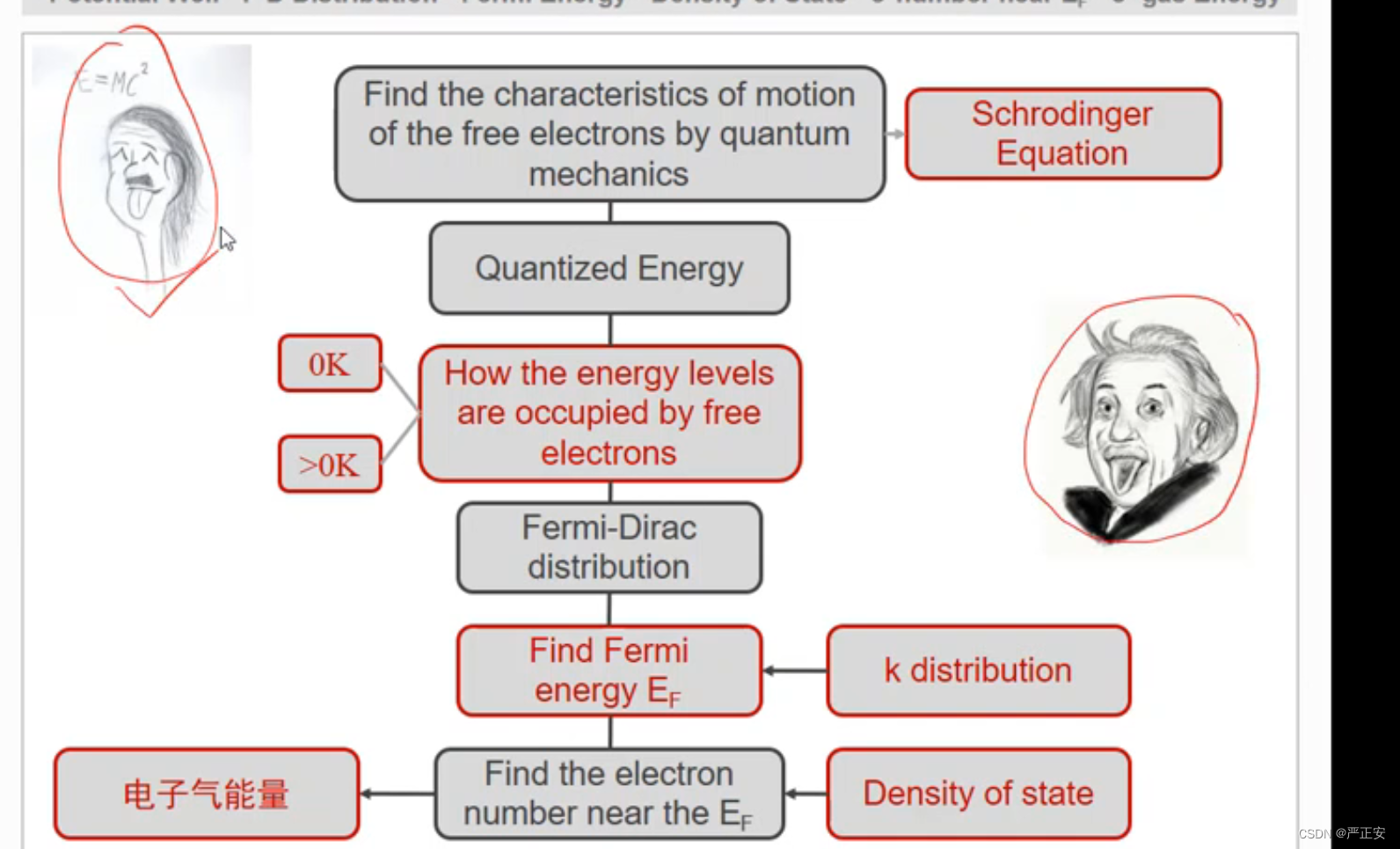
如何解释传统热容算出来的数值与量子模型下的区别？

CFE \ model \ predicts-> C_v =\frac{3}{2}R\\ \ \ experiments \ show -> C_v=10^{-4}RT

因为只有费米能附近的电子才能够进行移动，这个是问题的差别所在

我们下面就来介绍如何求费米能（费米能的计算）

既然费米能附近的电子很重要，那么附近的电子有多少很重要

我们需要波矢的分布和态密度

我们知道了

E=\frac{h^2 k^2}{2m}=\frac{h^2}{2m}(k_x^2+k_y^2+k_z^2) 

\vec k=k_x \vec i +k_y \vec j+k_z \vec l

k_x=\frac{2 \pi}{L} n_x,k_y=\frac{2 \pi}{L} n_y,k_z=\frac{2 \pi}{L} n_z

E=(n_x^2+n_y^2+n_z^2)E_0 =n^2 E_0,E_0=\frac{\pi^2 h^2}{2 m L^2}

如果落在一个球面上都具有相同的能量，K空间存在一个等能面

我们求解薛定谔方程的时候能量时量子化的

费米能在k空间的形状是一个球面，费米球的表面我们称之为费米面

费米球的半径称为费米波矢E_F=\frac{(hk_F)^2}{2m}

我们把

\rho (k)*V_{Fermi sphere}=N_{k}

\rho(k)=\frac{V}{8 \pi^3}

V_{F}\cdot \rho(k)=(\frac{4 \pi k_F^3}{3})(\frac{V}{8 \pi^3})=\frac{k_F^3}{6 \pi^2}V

Number \ of \ e^{-} N=2 \cdot \frac{k_F^3}{6 \pi^2}V

Density \ of \ e^{-} \ n=\frac{N}{V}=\frac{k_F^3}{3 \pi^2}

k_F = (3 \pi^2 n)^{\frac{1}{3}}

E_{F}^{0}=\frac{(\hbar k_F)^2}{2m}= \frac{ \hbar^2}{2m}(3 \pi^2 n)^{\frac{2}{3}}

n是自由电子密度，是一个本征量

 

我们下面找到费米能附近的电子数量，也就是电子随能量的分布情况

DOS:单位频率间隔独立格波的数目

在自由电子理论里面定义有所不同

DOS:单位能能量间隔电子的能态数量，用g(E)来表示

g(E)=\frac{dZ}{dE}

在半径k里面总的能态数量

Z(E)=2 \cdot \rho(k) \cdot \frac{4}{3} \pi k^3=\frac{Vk^3}{3 \pi^2}

g(E)=\frac{dZ}{dE}=\frac{dZ}{dk}\cdot \frac{dk}{dE}

g(E)=\frac{dZ}{dk}\cdot \frac{dk}{dE}=\frac{V}{ 2 \pi^2}\cdot \frac{2m}{\hbar^2}^{\frac{3}{2}} \cdot E^{\frac{1}{2}}

g(E)= C \cdot E^{\frac{1}{2}}

电子能量分布函数

N (E) 电子能量分布函数

N(E)=g(E) f(E)

g(E)是电子能态的数量，f(E)是占据该能态的概率

N=\int_{0}^{+\infty}g(E)f(E)dE

 

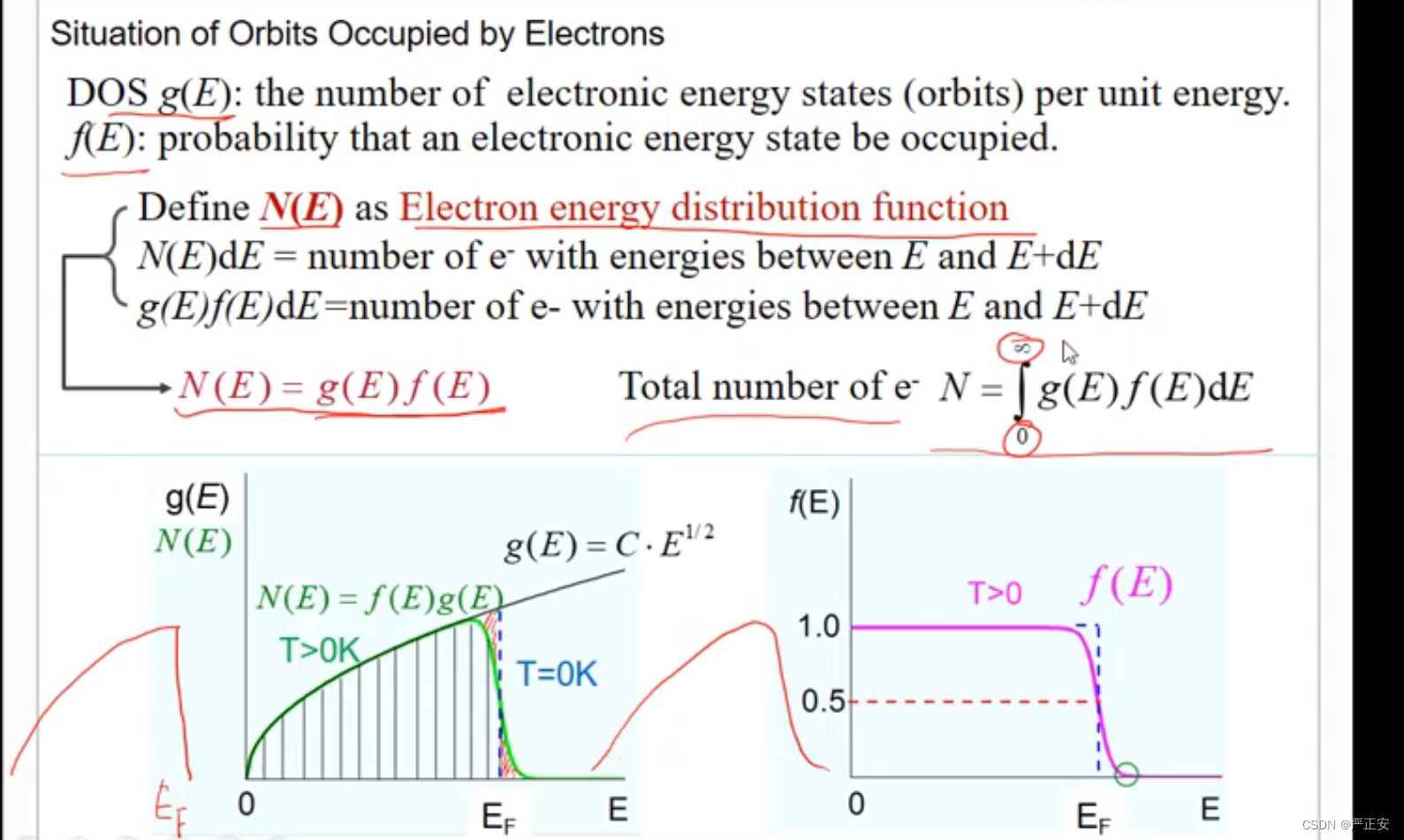
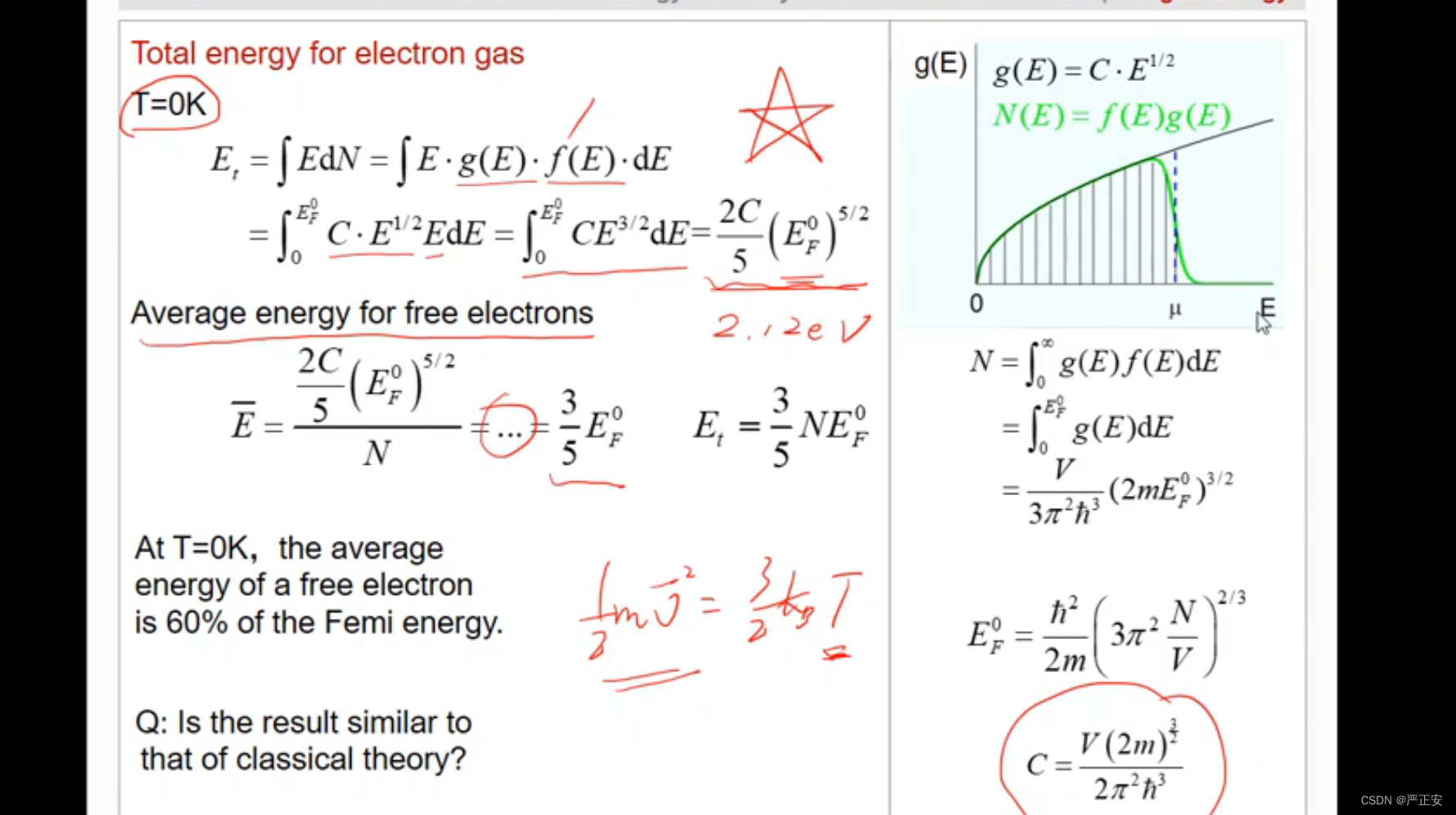
 T=0k的时候

E_t=\int E dN=\int E \cdot g(E) \cdot f(E)\cdot dE

=\frac{2C}{5}(E_F^0)^{\frac{5}{2}}

平均能量\overline E = \frac{3}{5} E_{F}^{0}

温度不为0k的时候，情况会变得稍微复杂一些

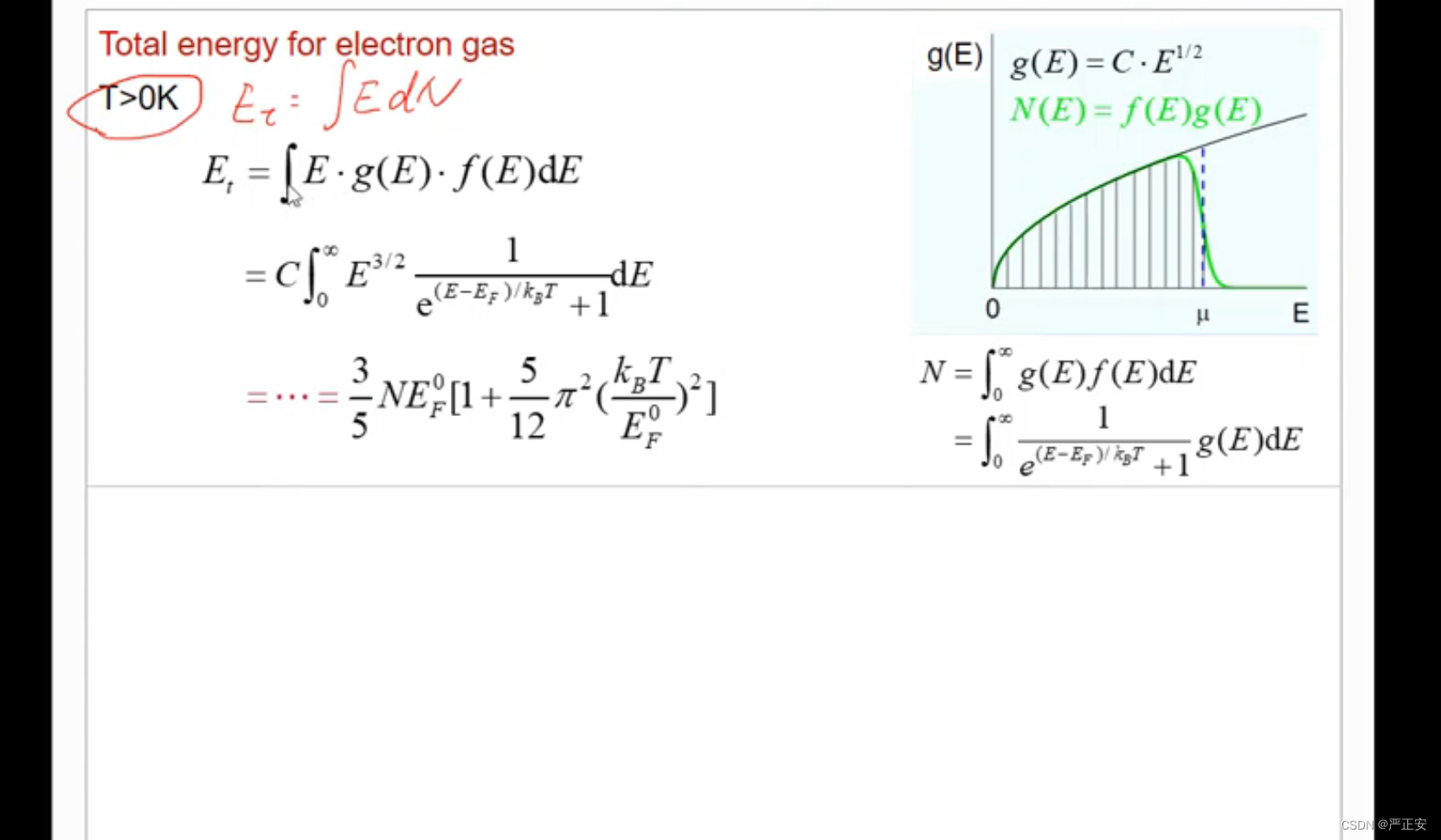
 我们可以把前面的称为零点能，随着温度的升高，电子气能量的增加都体现在后面的因子上面了

http://www.lryc.cn/news/25030.html

相关文章：

  • SAP ERP系统MM模块常用增强之四：采购申请输入字段的校验检查
  • STM32C0介绍(1)----概述
  • windows无盘启动技术开发之传统BIOS(Legacy BIOS)引导程序开发之一
  • mysql实现if语句判断功能的六种使用形式
  • 在Vue3这样子写页面更快更高效
  • 做软件测试，如何才能实现月入20K？
  • mysql last lesson
  • 一、Redis入门概述（是什么，能干嘛，去哪下，怎么玩）
  • （六十二）当我们在SQL里进行分组的时候，如何才能使用索引？
  • python字符串练习
  • Java-封装、继承、多态
  • 问题三十二：离散二维傅立叶变换（Discrete Fourier Transformation）
  • 恢复谷歌翻译的究极方法
  • string函数以及string常用接口
  • 分享一篇由C语言实现《数据结构》无头无循环单链表
  • C盘爆满？两个超简单的解决办法
  • ThreadLocal
  • Java基础:JDK7-时间Date
  • 什么是IP地址？
  • 4年经验之谈，什么是接口测试？怎样做接口测试？
  • 普通指针扫盲
  • 深度学习笔记：神经网络权重确定初始值方法
  • 关于 python 的异常使用说明 (python 的文件和异常)
  • Spark RDD持久化
  • 【Linux】Linux系统安装Python3和pip3
  • 用java进行base64加密
  • torch函数合集
  • AcWing算法提高课-3.1.2信使
  • Paddle OCR Win 11下的安装和简单使用教程
  • 杂谈：数组index问题和对象key问题