数据结构 -- 图论之最小生成树

目录

1.最小生成树算法

1.Kruskal算法

2.Prim算法

1.最小生成树算法

定义:最小生成树算法:连通图有n个顶点组成,那么此时的图的每一个点都能相互连接并且边的个数为n-1条,那么此时该图就是最小生成树.

下面量算法有几个共同的特点:

1.只能使用图中权值最小的边来构造生成树

2.只能使用恰好n-1条边构造生成树

3.n-1条边的图不能存在回路

4.Kruskal和Prim两个算法都采用了逐步求解的贪心策略

1.Kruskal算法

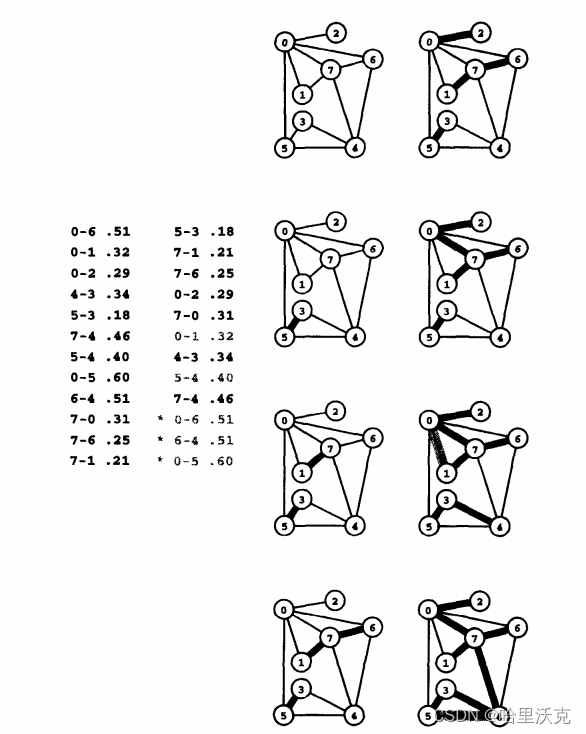
任给一个有n个顶点的连通网络N={V,E}，首先构造一个由这n个顶点组成、不含任何边的图G={V,NULL}，其中每个顶点自成一个连通分量，其次不断从E中取出权值最小的一条边(若有多条任取其一)，若该边的两个顶点来自不同的连通分量，则将此边加入到G中。如此重复，直到所有顶点在同一个连通分量上为止。核心：每次迭代时，选出一条具有最小权值，且两端点不在同一连通分量上的边，加入生成树。

		//数组的下标添加边void _AddEdge(size_t srci, size_t dsti, const W& w){_matrix[srci][dsti] = w;// 无向图if (Direction == false){_matrix[dsti][srci] = w;}}struct Edge{size_t _srci;size_t _dsti;W _w;Edge(size_t srci, size_t dsti, const W& w):_srci(srci), _dsti(dsti), _w(w){}bool operator>(const Edge _edge)const{return _w > e._w;}};W Kruskal(Self& minTree){size_t n = _vertexs.size();minTree._vertexs = _vertexs;minTree._indexMap = _indexMap;minTree._matrix.resize(n);for (size_t i = 0; i < n; ++i){minTree._matrix[i].resize(n, MAX_W);}priority_queue<Edge, vector<Edge>, greater<Edge>> minque;for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){if (i < j && _matrix[i][j] != MAX_W){minque.push(Edge(i, j, _matrix[i][j]));}}}int size = 0;W totalW = W();UnionFindSet ufs(n);while (!minque.empty()){Edge min = minque.top();minque.pop();if (!ufs.InSet(min._srci, min._dsti)){minTree._AddEdge(min._srci, min._dsti, min._w);ufs.Union(min._srci, min._dsti);++size;totalW += min._w;}}if (size == n - 1)return totalW;elsereturn W();}

2.Prim算法

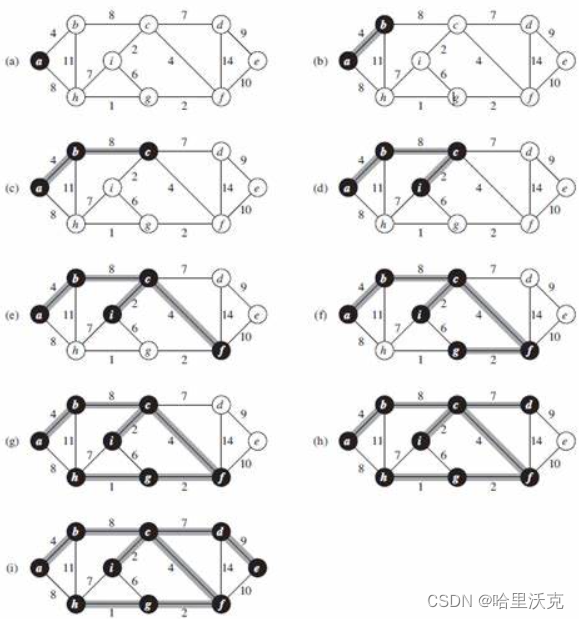
1.从源点出发，将所有与源点连接的点加入一个待处理的集合中

2.从集合中找出与源点的边中权重最小的点，从待处理的集合中移除标记为确定的点

3.将找到的点按照步骤1的方式处理

4.重复2，3步直到所有的点都被标记

(重点是不需要并查集来判断是否成环,因为两个集合就天然区分是否成环的因素)

		W Prim(Self& minTree,const V& src){size_t srci = GetVertexIndex(src);size_t n = _vertexs.size();minTree._vertexs = _vertexs;minTree._indexMap = _indexMap;minTree._matrix.resize(n);for (size_t i = 0; i < n; ++i){minTree._matrix[i].resize(n, MAX_W);}vector<bool> X(n, false);vector<bool> Y(n, true);X[srci] = true;Y[srci] = false;priority_queue<Edge, vector<Edge>, greater<Edge>> minq;for (int i = 0; i < n; ++i){if (_matrix[srci][i] != MAX_W){minq.push(Edge(srci, i, _matrix[srci][i]);}}size_t num = 0;W sum = W();while (!minq.empty()){Edge min = minq.top();minq.pop();if (!X[min._dsti]){minTree.AddEdge(min._srci, min._dsti, min._w);X.insert(min._dsti);Y.erase(min._dsti);++num;sum += min._w;if (num == n - 1) break;for (int i = 0; i < n; ++i){if (_matrix[min._dsti][i] != MAX_W && Y[i]){minq.push(Edge(min._dsti, i, _matrix[min._dsti][i]);}}}}if (num == n - 1)return sum;elsereturn W();}