当前位置：首页 > news >正文

leetCode 1080.根到叶路径上的不足节点 + 递归 + 图解

news 2025/9/15 21:33:17

给你二叉树的根节点 root 和一个整数 limit ，请你同时删除树中所有 不足节点 ，并返回最终二叉树的根节点。假如通过节点 node 的每种可能的 “根-叶” 路径上值的总和全都小于给定的 limit，则该节点被称之为 不足节点 ，需要被删除。叶子节点，就是没有子节点的节点。

示例 1：

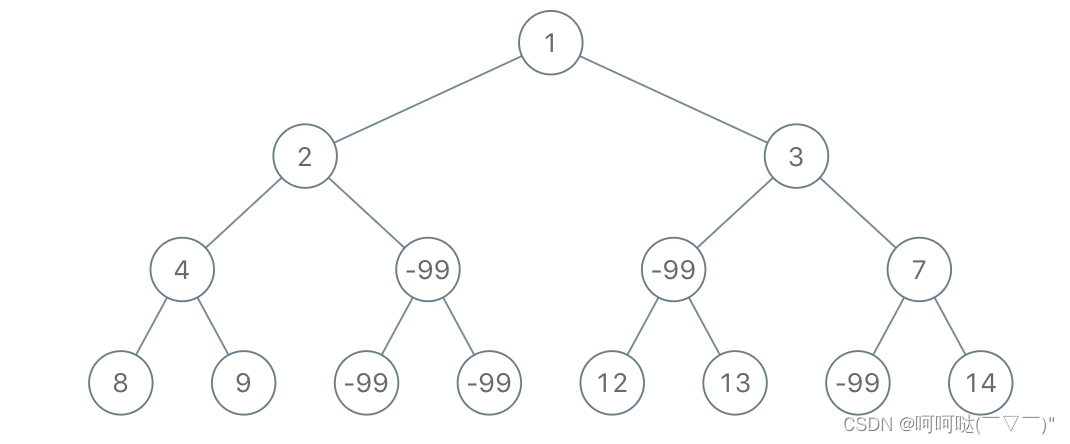
输入：root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1
输出：[1,2,3,4,null,null,7,8,9,null,14]

示例 2：

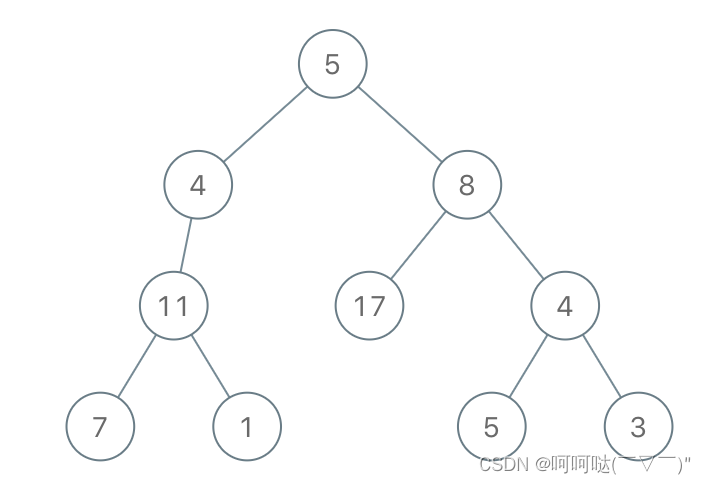
输入：root = [5,4,8,11,null,17,4,7,1,null,null,5,3], limit = 22
输出：[5,4,8,11,null,17,4,7,null,null,null,5]

示例 3：

输入：root = [1,2,-3,-5,null,4,null], limit = -1
输出：[1,null,-3,4]

方式1.添加一个递归参数 sumPath，表示从根到当前节点的路径和

(O_O)?疑惑：

① 叶子节点什么时候能删除？
② 非叶子节点若还有儿子未被删除，它能否被删除？
③ 非叶子节点的儿子都被删除，意味着什么？

思路和分析：

① 对于一个叶子节点（node），从根到这个叶子节点（leaf）的路径仅有一条，那么这条路径的元素和小于limit，就删掉该叶子节点
② 对于一个非叶子节点（node），若 node 还有儿子未被删除，那么 node 就不能被删除
- 反证法证明：设把 node 删除，那么经过 node 的所有路径和都小于 limit，这意味着经过 node 的儿子路径和也是小于 limit，那么 node 的儿子也应当被删除，矛盾！故 node 不能被删除
③ 对于一个非叶子节点（node）的儿子都被删除，意味着经过 node 的所有儿子的路径和都小于 limit。这等价于经过 node 的所有路径和都小于 limit，故 node 也应当被删除。
- 总结：当且仅当 node 的所有儿子都被删除，才可删除非叶节点 node

算法1：添加一个递归参数 sumPath,表示从根到当前节点的路径和

① 如果当前节点是叶子节点（leaf），且此时 sumPath < limit（说明从根到这个叶子节点的路径和小于limit），那么删除这个叶子节点
② 如果当前节点是非叶子节点（node），继续往下递归，node的左儿子（为leaf）时且经过 node 的左儿子路径和也是小于limit，就删除这个儿子；node的右儿子（为leaf）时且经过 node 的右儿子路径和也是小于limit，就删除这个儿子；

if(node->left && dfs(node->left,limit,sumPath)==false)  { // 左node->left = nullptr;
}

if(node->right && dfs(node->right,limit,sumPath)==false)  { // 右node->right = nullptr;
}

③ 如果当前节点是非叶子节点（node），且左右儿子都为空，那么就删除 node，返回 false ；否则，返回 true

return node->left || node->right;

C++代码：

class Solution {
public:bool dfs(TreeNode* node,int limit,int sumPath) {sumPath += node->val;if(node->left == node->right) {return sumPath>=limit;} if(node->left && dfs(node->left,limit,sumPath)==false)  { // 左node->left = nullptr;}if(node->right && dfs(node->right,limit,sumPath)==false)  { // 右node->right = nullptr;}return node->left || node->right;}TreeNode* sufficientSubset(TreeNode* root, int limit) {return dfs(root,limit,0) ?root:nullptr;}
};

① 图解示例一：

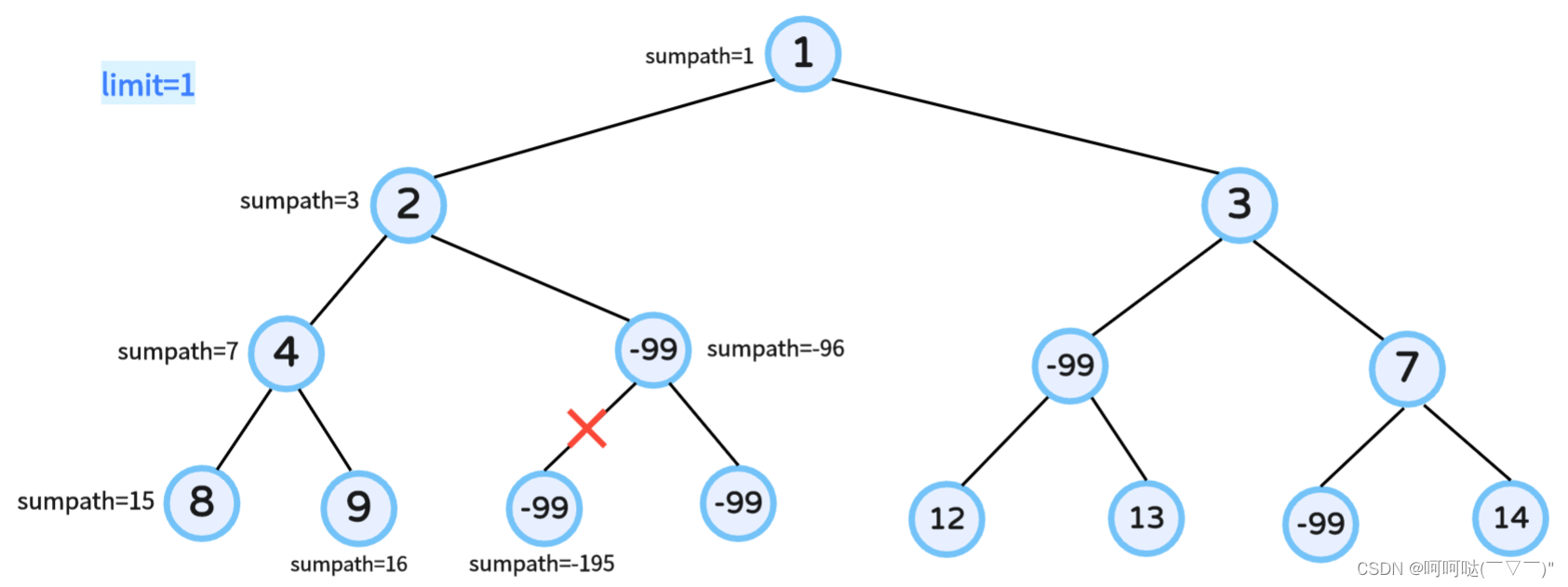
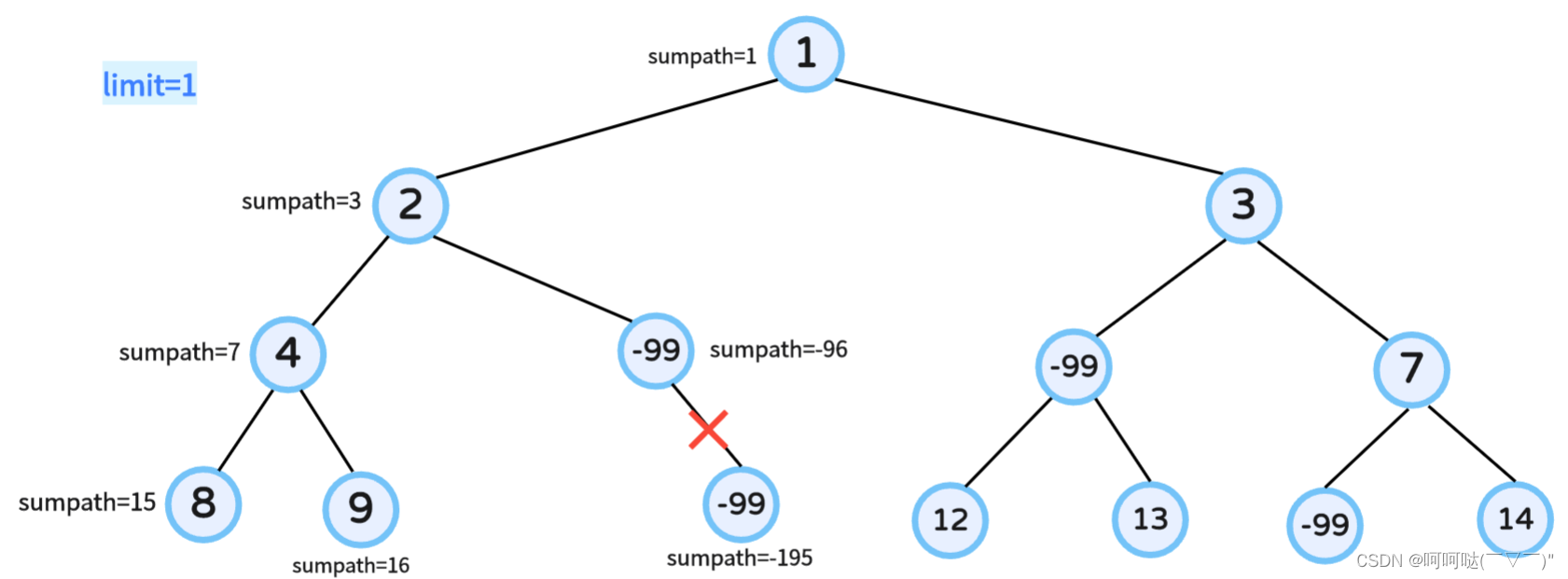
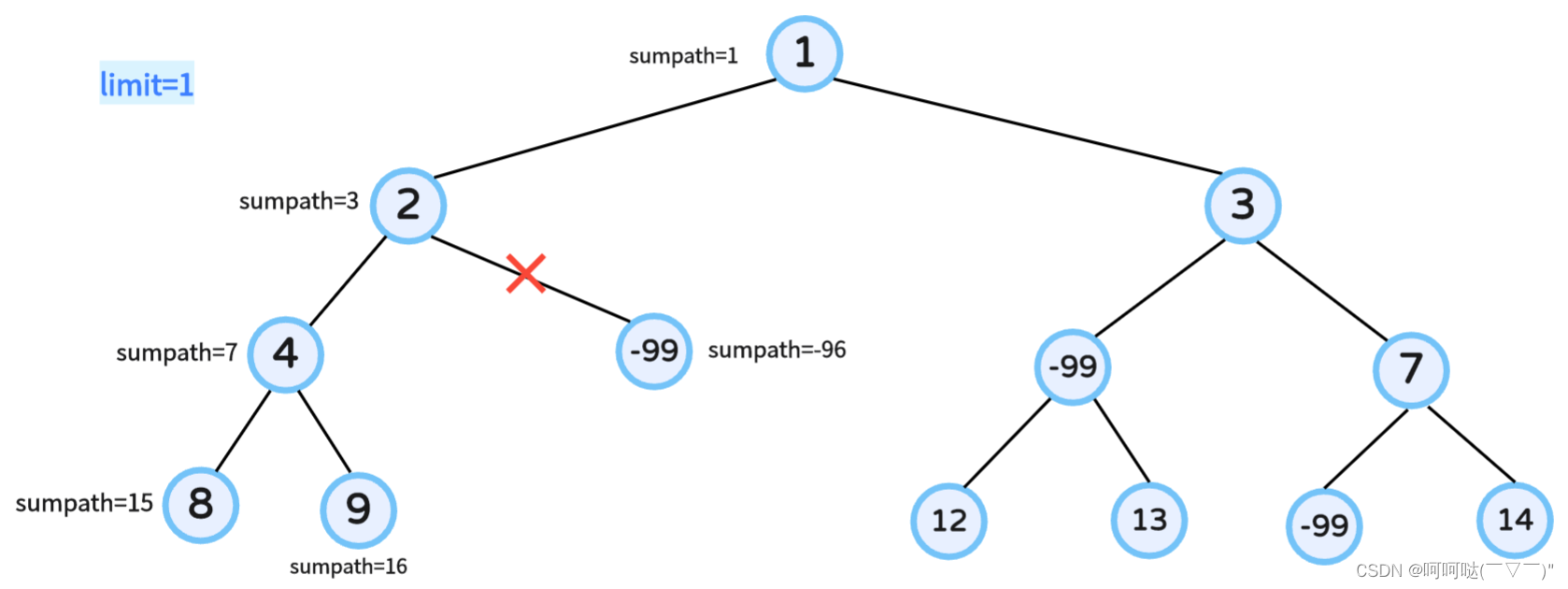
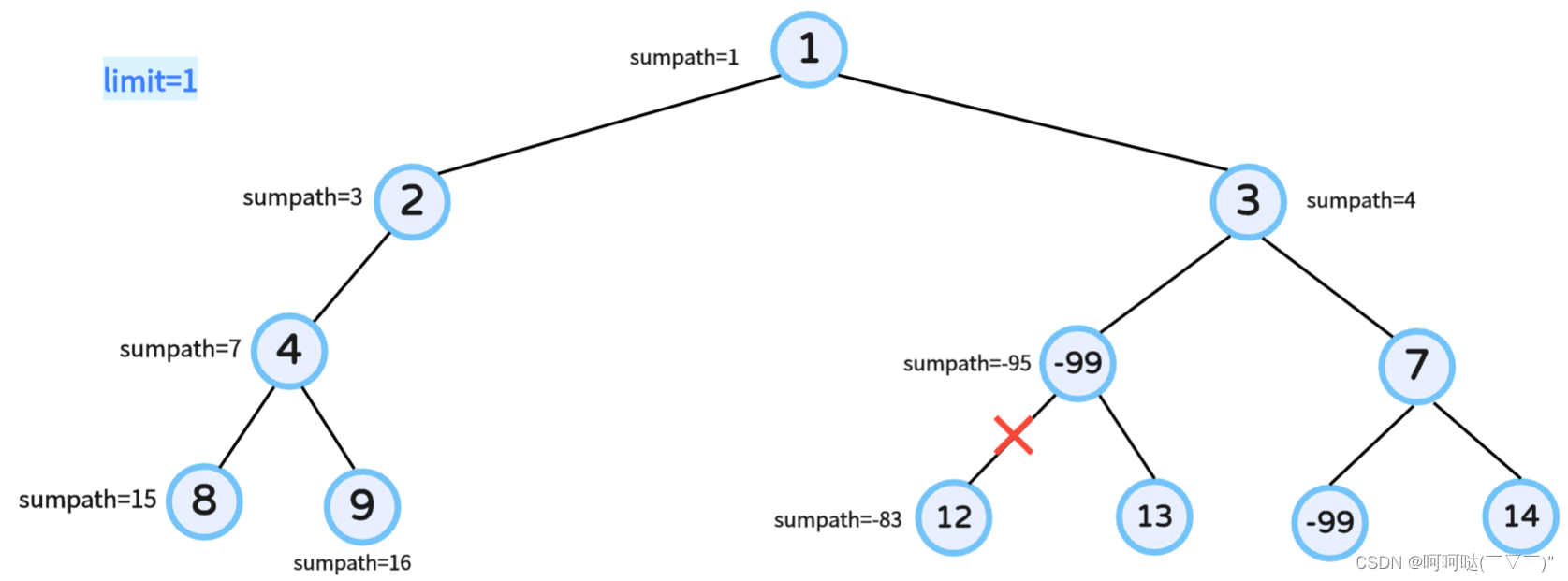
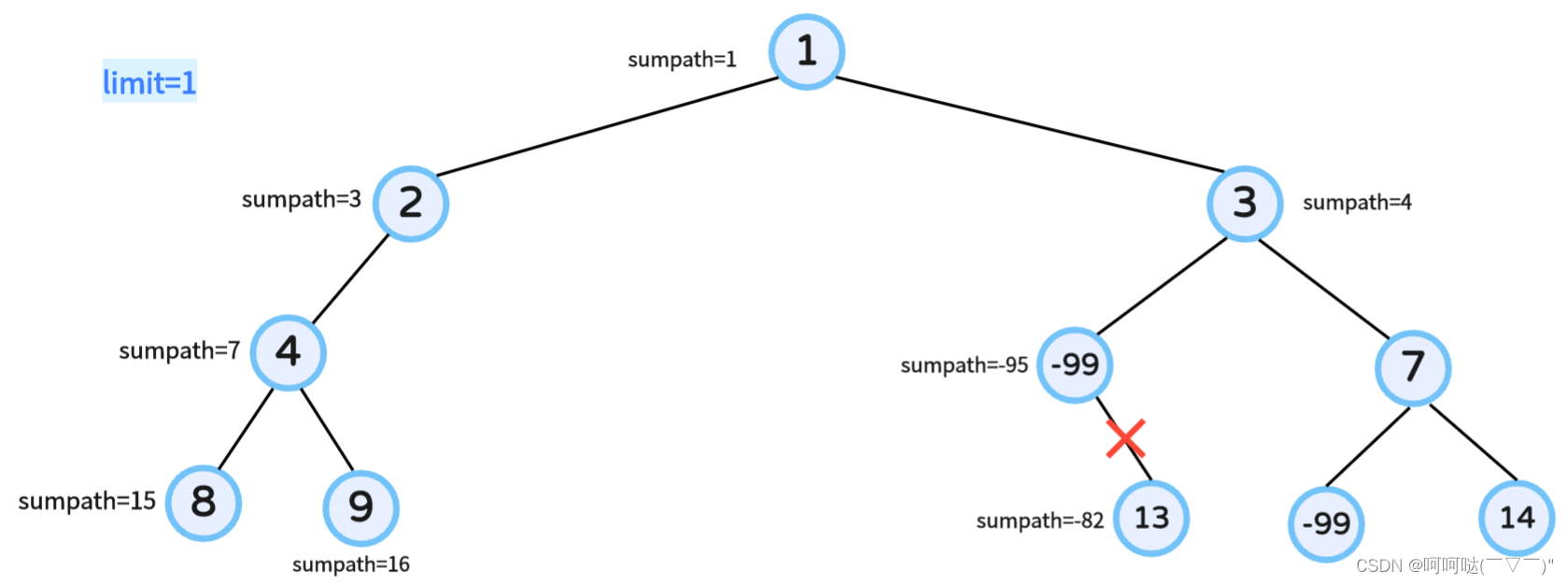
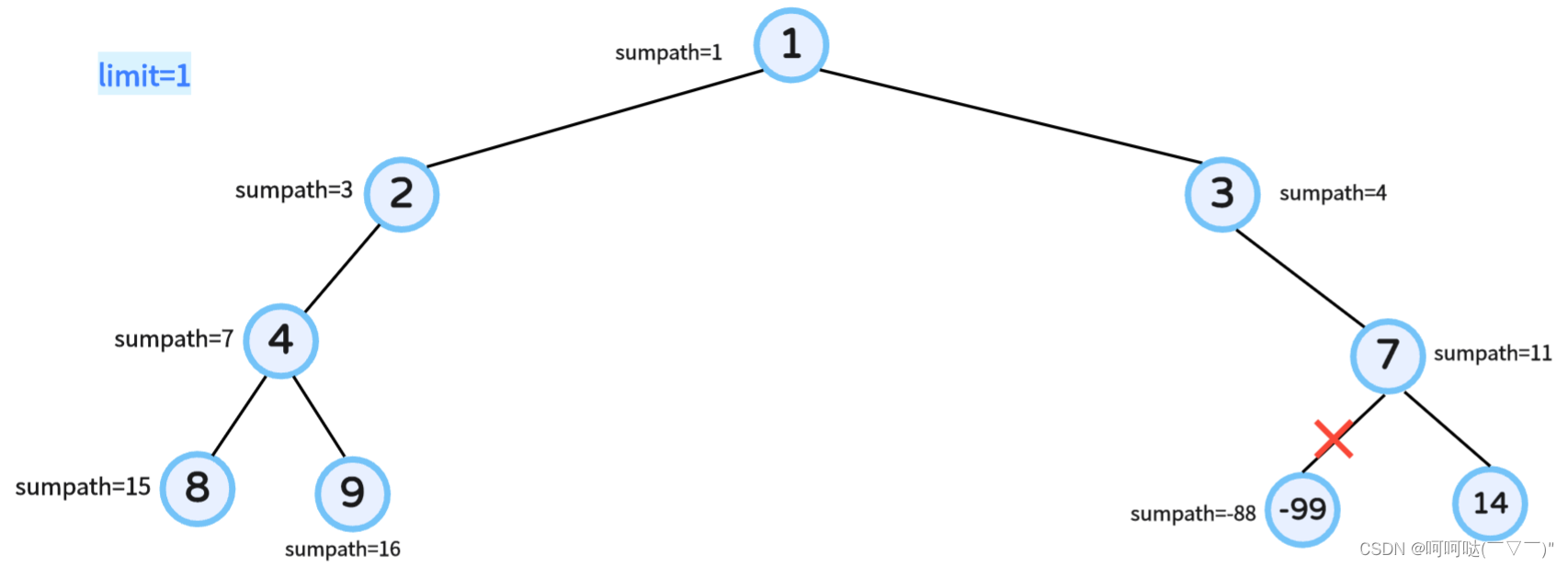
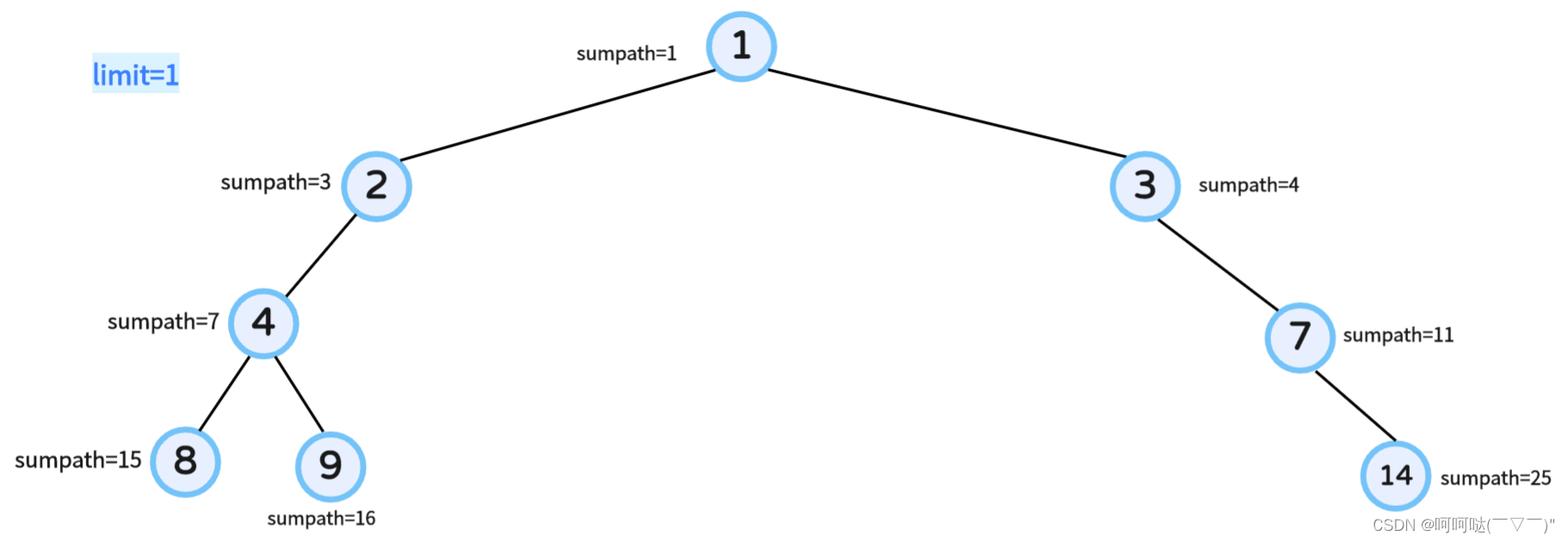
② 图解示例三：

方式2.从 limit 中减去当前节点值

先比方式1可以少一个参数 sumPath

class Solution {
public:bool dfs(TreeNode* node,int limit) {limit-=node->val;if(node->left == node->right) {return limit>0?false:true;} if(node->left && dfs(node->left,limit)==false)  { // 左node->left = nullptr;}if(node->right && dfs(node->right,limit)==false)  { // 右node->right = nullptr;}return node->left || node->right;}TreeNode* sufficientSubset(TreeNode* root, int limit) {return dfs(root,limit) ?root:nullptr;}
};

方式3. 从 limit 中减去当前节点值（直接调用 sufficientSubset）

如果当前节点是叶子，且此时 limit > 0，说明从根到这个叶子的路径和小于 limit ，那么删除这个叶子
如果当前节点不是叶子，那么往下递归，更新它的左儿子为对左儿子调用 sufficientSubset 的结果，更新它的右儿子为对右儿子调用 sufficientSubset 的结果
如果左右儿子都为空，那么就删除当前节点，返回空；否则不删，返回当前节点

此段文字来自以下作者

作者：灵茶山艾府
链接：https://leetcode.cn/problems/insufficient-nodes-in-root-to-leaf-paths/description/

class Solution {
public:TreeNode* sufficientSubset(TreeNode* root, int limit) {limit-=root->val;if(root->left == root->right) { // root 是叶子return limit > 0 ? nullptr : root;} if(root->left)  { // 左root->left = sufficientSubset(root->left,limit);}if(root->right)  { // 右root->right = sufficientSubset(root->right,limit);}// 如果有儿子没被删除，就不删 root，否则删 rootreturn root->left || root->right ?root:nullptr;}
};

（嘻嘻，仅供参考）自己又写了一个版本：

class Solution {
public:TreeNode* dfs(TreeNode* node,int limit,int sumPath) {sumPath += node->val;if(node->left == node->right) {return sumPath>=limit? node : nullptr;} if(node->left)  { // 左node->left = dfs(node->left,limit,sumPath);}if(node->right)  { // 右node->right = dfs(node->right,limit,sumPath);}return node->left || node->right ?node:nullptr;}TreeNode* sufficientSubset(TreeNode* root, int limit) {return dfs(root,limit,0) ? root:nullptr;}
};

参考和推荐文章：

1080. 根到叶路径上的不足节点 - 力扣（LeetCode）https://leetcode.cn/problems/insufficient-nodes-in-root-to-leaf-paths/solutions/2278769/jian-ji-xie-fa-diao-yong-zi-shen-pythonj-64lf/