6.15合并二叉树(LC617-E)
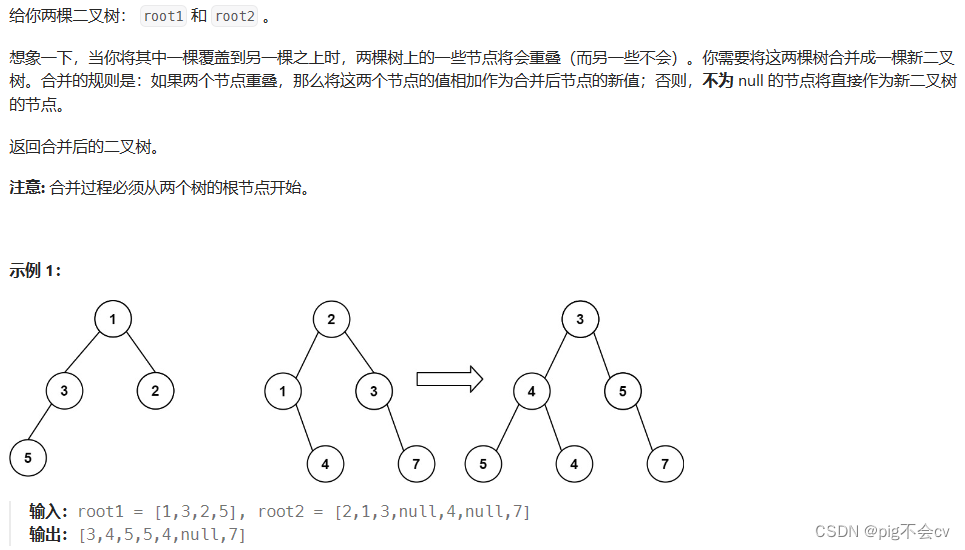
算法:
前序、中序、后序都可以,这道题正常逻辑一般都是用前序
正确代码:
这里就是在root1这颗树上改的,也可以新建一个树。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {if (root1 == null) return root2;if (root2 == null) return root1;root1.val += root2.val;root1.left = mergeTrees(root1.left, root2.left);root1.right = mergeTrees(root1.right, root2.right);return root1;}
}时间空间复杂度:
时间复杂度分析
- 在每个节点上,只进行了常数时间的操作,比如节点值的相加和指针的赋值。因此,每个节点的操作时间复杂度为 O(1)。
- 在最坏情况下,需要遍历两棵树的所有节点。因此,整个合并过程的时间复杂度为O(n),其中 n 是两棵树中节点的总数。
空间复杂度分析
- 递归调用的深度最坏情况下为树的高度,因此空间复杂度为O(ℎ),其中 ℎ 是树的高度。
- 在最坏情况下,如果树是完全不平衡的,高度可以达到 n,其中 n 是树中节点的总数。因此,空间复杂度为O(n)。
因此,该算法的时间复杂度为O(n),空间复杂度为O(n)。
