【Day02数据结构 空间复杂度】
最近太忙了都好久没有更新博客了,太难了
,抽空水一篇文章,大佬们多多支持.
上篇:时间复杂度分析
目录
前言
一、空间复杂度概念?
二、实例展示
三、.有复杂度要求的算法题练习
1.题目链接:力扣--消失的数字
2.题目链接:力扣--旋转数组
总结:
1.空间复杂度
2.有关空间复杂度的OJ题
前言
上节我们学习了算法的时间复杂度,今天来学习空间复杂度.
一、空间复杂度概念?
老规矩先上定义:
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。前一篇关于时间复杂度我们知道 计算空间复杂度并不是计算算法的执行时间,算的是算法的执行次数,而空间复杂度同理,不算空间,算的是变量的个数.它同样和时间复杂度一样是一个估算,与时间复杂度的规定大同小异.
二、实例展示
1.冒泡排序:
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}解析:空间复杂度也是用大O渐进法,类似于时间复杂度的方式,是去计算变量的个数, 如上冒泡排序的空间复杂度是O(1) ,变量有 a,n,szie_t end,size_t i,exchange.总共是常数5个,常数都看作是 1,所以空间复杂度是O(1).
这里我们要注意,时间是可以累计的,而空间是不累计的,也就是说时间用完了还存在,而空间被开辟后用完可以丢弃销毁,比如:一个循环走了N次,它重复利用的是一个空间.用不到了就可以被销毁;递归同样也是一个道理,在递归时开辟了一块又一块的空间,当计算往下走时,保留空间,返回时,用不到的空间就会被销毁.
2.斐波那契数:
// 计算Fibonacci的空间复杂度?
long long* Fibonacci(size_t n)
{if(n==0)return NULL;long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; ++i){fibArray[i ] = fibArray[ i - 1] + fibArray [i - 2];}return fibArray ;
}解析:(malloc的意思是开辟了 n+1 个 long long 类型变量的数组).
计算变量个数有 n, fibArray, fibArray[0], fibArray[1], i 一共 5 个,但是我们还看见 malloc 函数中有 (n+1) ,所以空间复杂度是 O(N+6) ,随着N的增大, +6 的影响对其影响不大,所以可以忽略不计,最后斐波那契数的空间复杂度是 O(N) .
(大多数情况下,算法的空间复杂度都是O(1),都是常数个变量,此代码中 malloc 是开辟了一个数组.)
3.阶乘递归:
// 计算阶乘递归Factorial的空间复杂度?
long long Factorial(size_t N)
{return N < 2 ? N : Factorial(N-1)*N;
}解析: 这个代码我们知道,递归调用了 N 次,每一次都调用建立一个栈帧,每个栈帧使用了常数个空间,也就是一次递归的空间复杂度是 O(1) ,而调用了 N 次递归,空间复杂度就是 O(N) .
(虽然递归调用返回时空间销毁,但是我们仍要计算它,可以理解为计算时间复杂度的最坏情况,)
三、.有复杂度要求的算法题练习
1.题目链接:力扣--消失的数字

思路一:
数组nums包含 0 ~ n 的所有整数,要找出其中缺的那一个数字,我们按将其数组元素进行排序,例如: [2 ,3, 1, 4, 5, 7, 6, 9],将其排序之后就会变成[1,2,3,4,5,6,7,9].然后就很简单了,要找到消失的数就可以将排序后的元素遍历一遍,看后一个数是不是比前一个数大1,如果不是那就直接找到了.
代码如下:
int missingNumber(int* nums, int numsSize){for(int i = numsSize - 1; i > 0; i--){//冒泡排序flag = 1;for(int j = 0; j < i; j++){if(nums[i] > nums[i + 1]){int tmp = nums[i];nums[i] = nums[i + 1];nums[i + 1] = tmp;if(flag)flag = 0;}if(flag)break;}}//检查每个元素前后是否相差为1for(int z = 0; z < numsSize - 2; z++){if(nums[z + 1] - nums[z] != 1)return nums[z + 1] - 1;} //考虑头尾if(nums[0])return 0;return numsSize;
}但是题目要求算法的时间复杂度要求是 O(N) ,如果使用最快的排序只能达到O(N*logN),所以排序并不合适.
思路二:
要求 0 ~ n 中缺失的那个,可以将 0 ~ n 的所有元素相加,得到的结果再与原数组里元素的和相减,结果就得到消失的数字.
代码如下:
int missingNumber(int* nums, int numsSize){int misNum = 0;for(int j = 0; j < numsSize + 1; j++)misNum += j;for(int i = 0; i < numsSize; i++)misNum -= nums[i];return misNum;
}思路三:
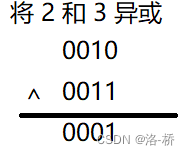
异或:将数组中的数依次跟 0 ~ n 的所有数异或,最后剩下的数据就是缺的那个数字(异或:按位异或相同为 0 ,不同为 1 ).
举例如下:
我们知道相同的数异或到一起就没了,是0. 此题如果把 0 ~ n 的数与原数组里的元素进行异或,然后相同的两个数异或没了,那么剩下的就是消失的那个数,(两数组进行异或时不需要有序,因为异或满足交换律,相同的会消失,最后剩下的就是要求的数)
举例验证:
这个例子我们可以看到虽然数据没有有序,但是相同的两个数被相互消去,得到的是不同的那个数.
代码如下:
int missingNumber(int* nums, int numsSize){int x = 0;//用for循环求出数组中的异或之和for(int i = 0; i < numsSize; i++)x ^= nums[i];for(int j = 0; j < numsSize + 1; j++)//原数组比0~n少1个数,要+1//再和(0~n)之间的数异或x ^= j;return x;
}2.题目链接:力扣--旋转数组
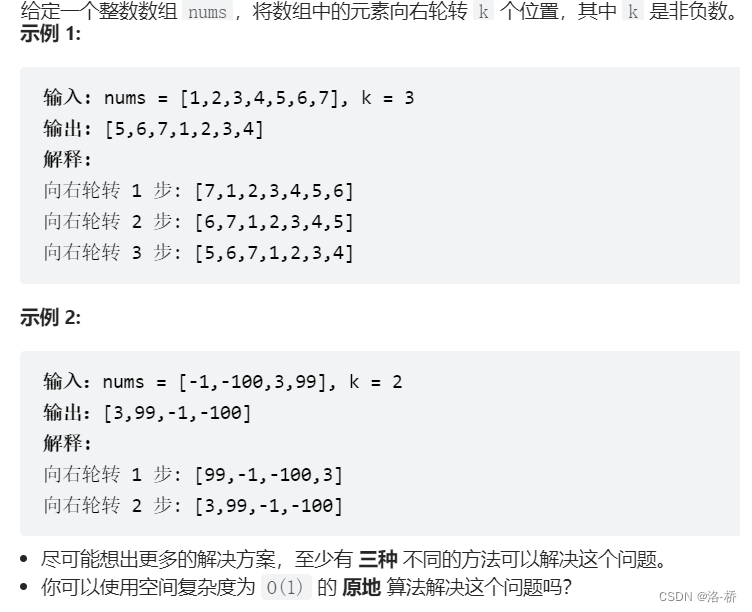
思路一:
如果要进行一次旋转,有数组 [1,2,3,4,5,6,7,8,9] ,可以先将数组中的最后末尾元素 9 存放到一个变量中,然后将最后一个元素之前的数据依次向后挪动,我们可以定义一个变量 end ,将它依次减减,就可以将元素依次挪动,直到最后首元素空出,再将 9 放进去,这样就完成了旋转了一次,
代码如下:
void rotate(int* nums, int numsSize, int k)
{for(int i=0;i<k;++i ){//旋转一次int tmp=0;tmp=nums[numsSize-1];for(int end=numsSize-2;end>=0;end--){nums[end+1]=nums[end];}nums[0]=tmp;}
}当前代码的时间复杂度是O(N*K),效率太低.
思路二:
以空间换时间:创建一个新的数组,首先将后 k 个数放到新数组的前 k 项里面,然后再将剩下的数放到新数组里面,(也就是将原数组分两段存放到一个新的数组中)
最后第二个循环是将新数组的内容替换掉原数组中的内容
代码如下:
void rotate(int* nums, int numsSize, int k){int nums1[numsSize];for(int i=0;i<numsSize;i++){nums1[(i+k)%numsSize]=nums[i];}for(int j=0;j<numsSize;j++){nums[j]=nums1[j];}
}numsSize取余是为了防止k的大小长度超过numsSize, 这样的解法时间复杂度符合要求,但是需要额外的空间实现
思路三:
有数组 [1,2,3,4,5,6,7]
先将数组的后 k 个逆置: [1,2,3,4,7,6,5]
再将前 n - k 个逆置: [4,3,2,1,7,6,5]
再整体逆置:[5,6,7,1,2,3,4]
代码如下:
void Reverse(int* nums, int left, int right)
{while (left < right){int tmp = nums[left];nums[left] = nums[right];nums[right] = tmp;++left;--right;}
}
void rotate(int* nums, int numsSize, int k)
{if (k >= numsSize){k %= numsSize;}Reverse(nums, numsSize - k, numsSize - 1);Reverse(nums, 0 , numsSize -k - 1);Reverse(nums, 0 , numsSize - 1);}总结:
1.空间复杂度
2.有关空间复杂度的OJ题
仓促之下水的文章,码文不易,各位看官给个三连呗,如有不足还望指出.