数据挖掘之PCA-主成分分析
PCA的用处:找出反应数据中最大变差的投影(就是拉的最开)。
在减少需要分析的指标同时,尽量减少原指标包含信息的损失,以达到对所收集数据进行全面分析的目的
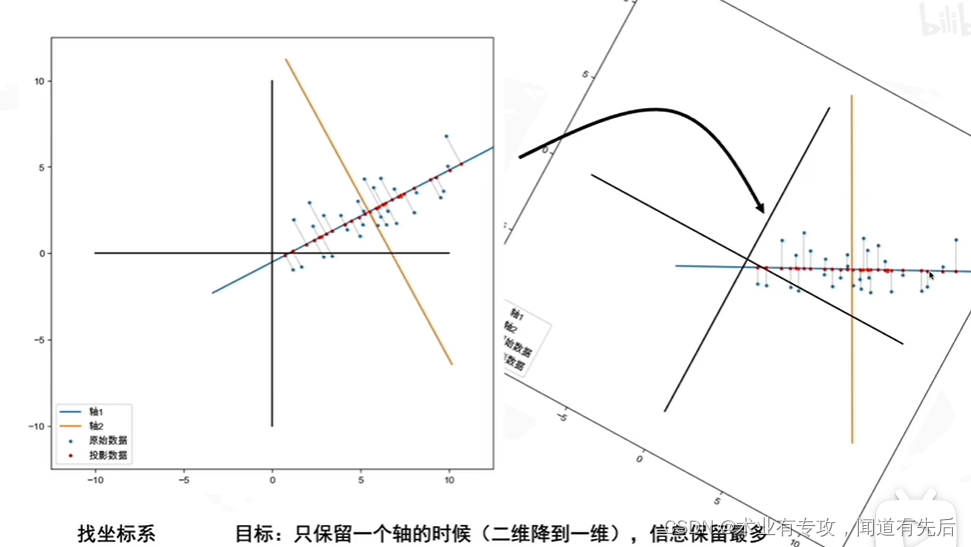
但是什么时候信息保留的最多呢?具体一点?

首先:去中心化(把坐标原点放到数据中心,如上图所示)
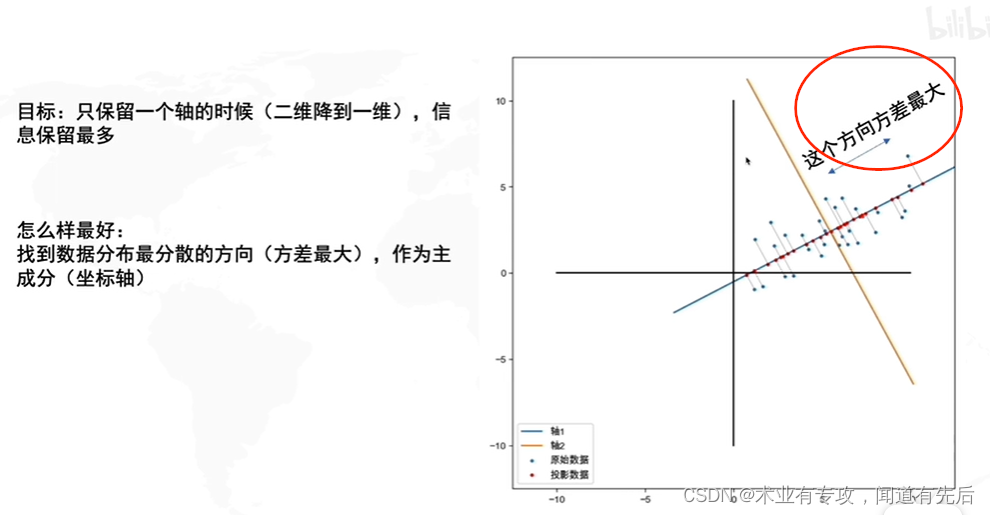
然后,找坐标系(找到方差最大的方向)
问题是:怎么找到方差最大的方向呢????????
一.引子
1.使用矩阵可以进行数据的线性变换(数据的拉伸)

2.使用矩阵可以进行数据的线性变换(数据的旋转)
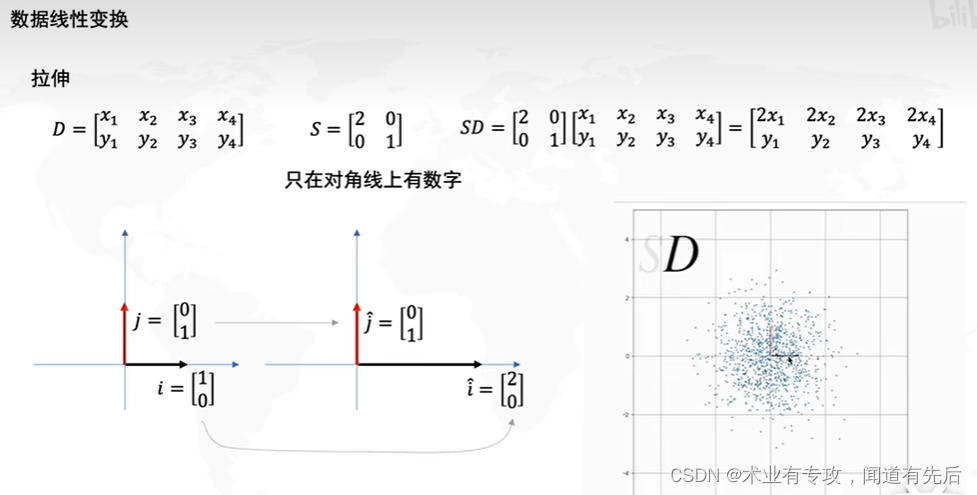
3.结合起来两种操作
拉伸决定了方差最大的方向是横或者纵
旋转决定了方差最大的方向的角度
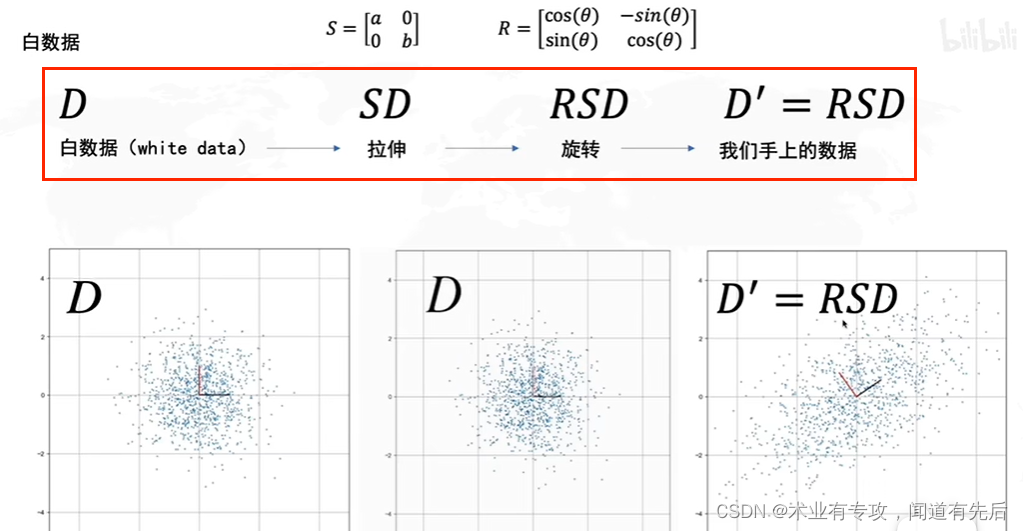
怎么求R?
协方差矩阵的特征向量就是R

二.数学原理:



三.PCA流程图:
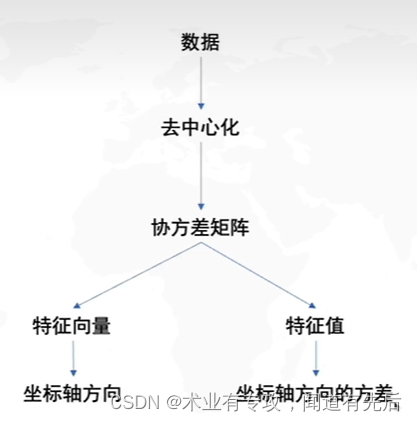
PCA与SVD的联系:

四.例子:



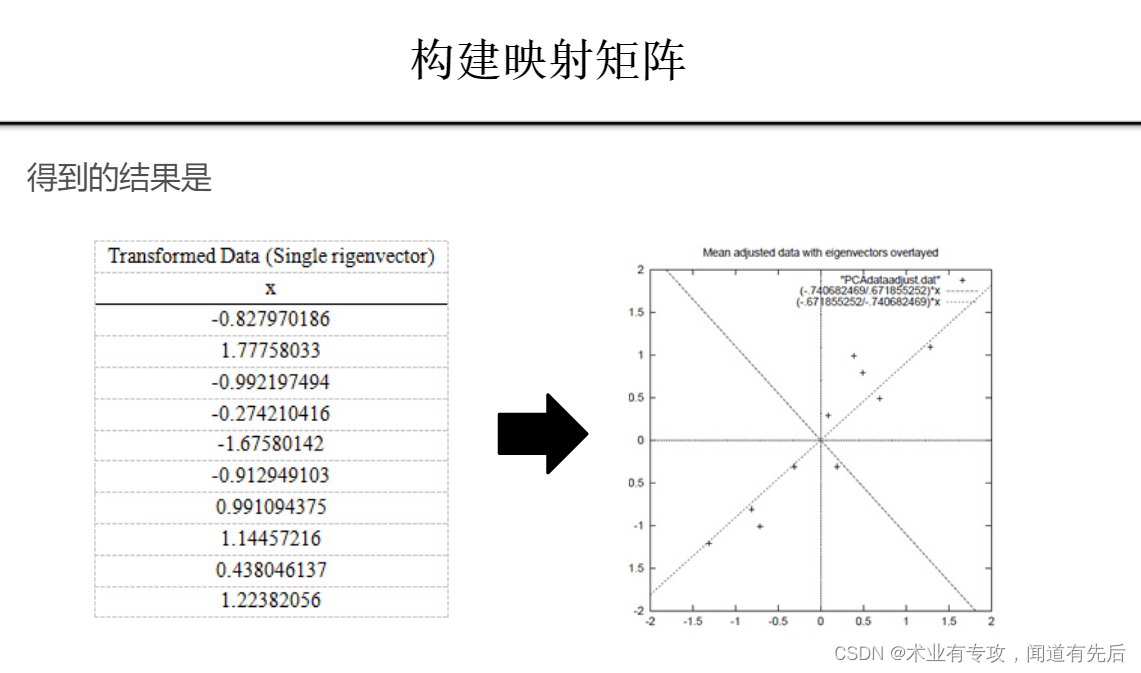
五.代码:
# -*- coding: utf-8 -*-
"""
Created on Tue Oct 13 11:12:24 2020@author: pc① 对原数据集零均值化。代码是:meanRemoved = dataMat - mean(dataMat,axis=0)② 求出均值化X的协方差矩阵:公式是:Cov(X)=\frac{1}{m-1}X^{T}X,代码是:covMat = cov(meanRemoved,rowvar=0)③ 求这个协方差矩阵的特征值,特征向量,代码是:eigVals, eigVects = linalg.eig(mat(covMat))④ 把这些特征值按从大到小排列,返回特征值的下标,代码是:eigValInd = argsort(-eigVals)⑤ 选出前topNfeat个特征值,返回这些选中的特征值的下标,并根据下标从特征向量矩阵eigVects中取出这些选中的特征向量组成矩阵P,这就是我们要找的变换矩阵P,代码是:redEigVects = eigVects[:,eigValInd[:topNfeat] ]⑥ 返回降维后的数据,公式是:Y=X•P,代码是:lowDDataMat = meanRemoved * redEigVects⑦ 原数据映射到新的空间中。公式是:X^{'}=Y\cdot P^{T}+mean,代码是:reconMat = (lowDDataMat * redEigVects.T) + meanValues
"""import numpy as np
import matplotlib.pyplot as pltdef pca(dataMat, topNfeat = 999999):meanValues = np.mean(dataMat,axis=0) # 竖着求平均值,数据格式是m×nmeanRemoved = dataMat - meanValues # 0均值化 m×n维covMat = np.cov(meanRemoved,rowvar=0) # 每一列作为一个独立变量求协方差 n×n维eigVals, eigVects = np.linalg.eig(np.mat(covMat)) # 求特征值和特征向量 eigVects是n×n维eigValInd = np.argsort(-eigVals) # 特征值由大到小排序,eigValInd十个arrary数组 1×n维eigValInd = eigValInd[:topNfeat] # 选取前topNfeat个特征值的序号 1×r维print(eigValInd)redEigVects = eigVects[:,eigValInd] # 把符合条件的几列特征筛选出来组成P n×r维lowDDataMat = meanRemoved * redEigVects # 矩阵点乘筛选的特征向量矩阵 m×r维 公式Y=X*PreconMat = (lowDDataMat * redEigVects.T) + meanValues # 转换新空间的数据 m×n维return lowDDataMat, reconMatdef drawPoints(dataset1,dataset2): # 画图,dataset1是没降维的数据,dataset2是数据映射到新空间的数据fig = plt.figure()ax1 = fig.add_subplot(211)ax2 = fig.add_subplot(212)ax1.scatter(dataset1[:,0],dataset1[:,1],marker='s',s=5,color='red')dataset2 = np.array(dataset2)ax2.scatter(dataset2[:,0],dataset2[:,1],s=5,color='blue')plt.show()if __name__ == '__main__':dataSetList = []fr = open('pca_data_set1.txt')for row in fr.readlines():cur_line = row.strip().split('\t')proce_line = list(map(float,cur_line))dataSetList.append(proce_line)dataSetList = np.array(dataSetList)data = dataSetListproccess_data, reconMat = pca(data,topNfeat = 1)drawPoints(data,reconMat)
