LeetCode 700. 二叉搜索树中的搜索
LeetCode 700. 二叉搜索树中的搜索
难度:easy\color{Green}{easy}easy
难度:middle\color{orange}{middle}middle
难度:hard\color{red}{hard}hard
题目描述
给定二叉搜索树(BST)的根节点 rootrootroot 和一个整数值 valvalval。
你需要在 BST 中找到节点值等于 valvalval 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 nullnullnull 。
示例 1:
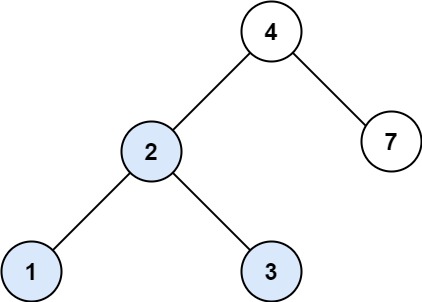
输入:root = [4,2,7,1,3], val = 2
输出:[2,1,3]
示例 2:
[外链图片转存中…(img-QAZGWobk-1677565545106)]
输入:root = [4,2,7,1,3], val = 5
输出:[]
提示:
- 数中节点数在 [1,5000][1, 5000][1,5000] 范围内
- 1<=Node.val<=1071 <= Node.val <= 10^{7}1<=Node.val<=107
- rootrootroot 是二叉搜索树
- 1<=val<=1071 <= val <= 10^{7}1<=val<=107
算法1
(递归)
二叉搜索树满足如下性质:
- 左子树所有节点的元素值均小于根的元素值;
- 右子树所有节点的元素值均大于根的元素值。
据此可以得到如下算法:
- 若 root 为空则返回空节点;
- 若 val=root.val,则返回 root;
- 若 val<root.val,递归左子树;
- 若 val>root.val,递归右子树。
复杂度分析
-
时间复杂度:O(n)O(n)O(n),其中 nnn 是二叉搜索树的节点数。
-
空间复杂度 : O(n)O(n)O(n)
C++ 代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {if (!root) return NULL;if (root->val == val) return root;if (root->val > val) return searchBST(root->left, val);else return searchBST(root->right, val);}
};
算法2
(迭代)
二叉搜索树满足如下性质:
- 左子树所有节点的元素值均小于根的元素值;
- 右子树所有节点的元素值均大于根的元素值。
据此可以得到如下算法:
- 若 root 为空则跳出循环,并返回空节点;
- 若 val=root.val,则返回 root;
- 若 val<root.val,将 root 置为 root.left;
- 若 val>root.val,将 root 置为 root.right。
复杂度分析
-
时间复杂度:O(n)O(n)O(n),其中 nnn 是二叉搜索树的节点数。
-
空间复杂度 : O(1)O(1)O(1)
C++ 代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {while (root) {if (root->val == val) return root;else if (root->val > val) root = root->left;else root = root->right;}return nullptr;}
};
