线性代数学习-2
线性代数学习-2
- 矩阵消元
- 消元
- 回代
- 消元矩阵
- 置换矩阵
- 逆矩阵
本文转载于https://herosunly.blog.csdn.net/article/details/88713747
该文章本人认为十分有用,便自己敲一遍笔记加固印象
原文链接 原文
这个笔记感觉比我老师讲的更加透彻,清晰。很好的展示了线性代数的原理,强烈推荐看原文
上篇文章讲的是如何从定型的方式(列向量)分析出对于任意的b,是的Ax=b有解。这片文章则具体讲解如何求Ax=b方程组的解。简单总结如下,主要是讲定性问题转换成定量解决
矩阵消元
消元
高斯消元法是计算机软件求解线性方程组最常用的方法。高斯消元法就是通过对方程组中的某两个方程进行适当的数乘和加法(线性空间的两大基本运算),以达到将某一个未知数系数变为零,从而削减未知数的目的。其中每一步的目标是消除未知数(保证主元不为零的前提下)。
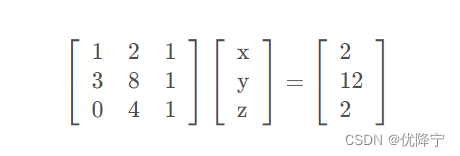
我们将矩阵左上角的1称之为**“主元一”(最好都是1),第一步要通过消元将第一列中除了住院之外的数字均变化为0.操作方法就是用之后的每一行减去第一行的适当倍数**,此例中第二行应减去第一行的3倍。之后应对第三行做类似操作,本例中三行第一列数字已经为0,故不用进行操作
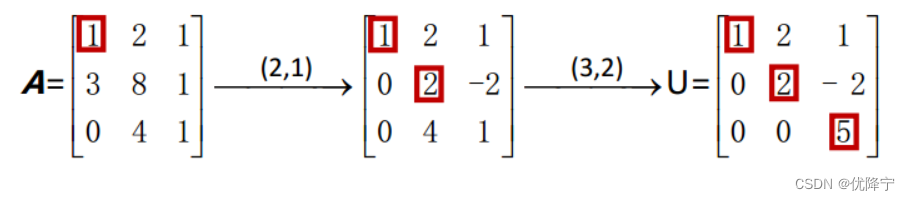
处在第二行第二列的主元为2,因此用第三行减去第二行的两倍进行消元,得到第三个主元为5.
矩阵A为可逆矩阵,消元结束后得到上三角阵U,即主对角线以下都是零的方阵成为上三角矩阵。
其左侧下半部分的元素均为0,而主元1、2、5分列在U的对角线上。主元之积即行列式的值(行列式只是方阵的一个性质)。
回代
做方程的高斯消元时,需要对等式右侧的b做同样的加法和数乘运算。手工计算时中比较有效率的方法是应用“增广矩阵”,将b插入矩阵的最后一列,然后进行相应的运算。
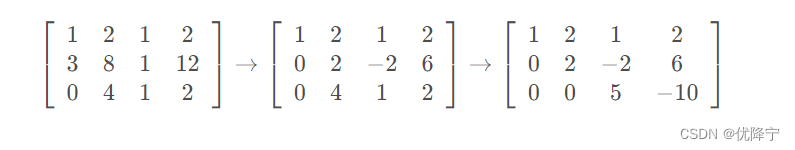
此时我们将原方程Ax=b转化成了新的方程Ux=从,其中c=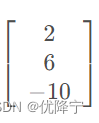
从最后一行得到z=-2,依次回代可以得到x=2和y=1。以上高斯消元的求解线性方程步骤。在线性代数中比较重要的就是将之前所说的“第二行减去第一行的3倍”这种操作条例变为矩阵化的数学语言。
消元矩阵
矩阵运算的核心内容就是对“行”或者“列”进行独立操作
如前文“列图像”,系数矩阵乘以未知数向量,相当于对系数矩阵的列向量进行线性组合。矩阵乘以列向量
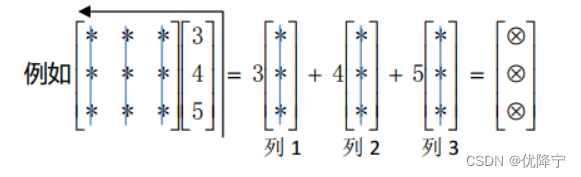
与之相对称,矩阵左乘行向量则是对矩阵的行向量进行线性组合。
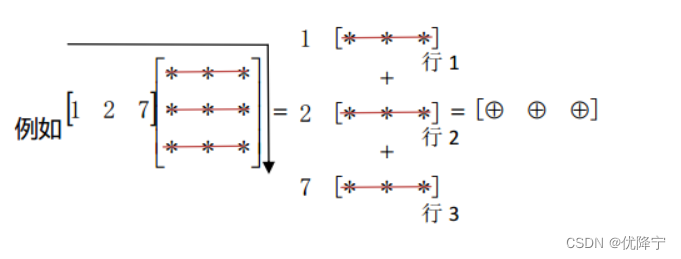
“列”操作就像是把向量开进矩阵,而“行操作”这个就像把向量倒车进入矩阵(如图中箭头所示)
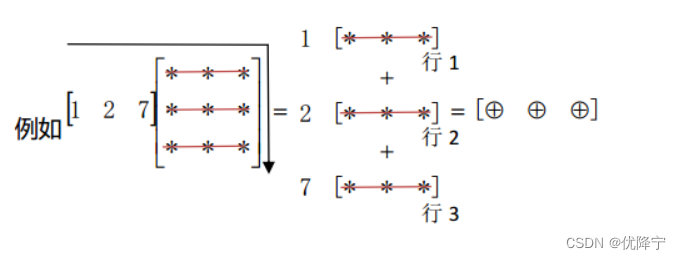



本质一样,但是这个计算介绍理解方法与教科书上相比简单很多
置换矩阵
置换矩阵的本质就是左乘或者右乘某个矩阵,从而完成行变换或者列变换
左乘置换矩阵可以完成原矩阵的行变换,右乘置换矩阵则为列变换
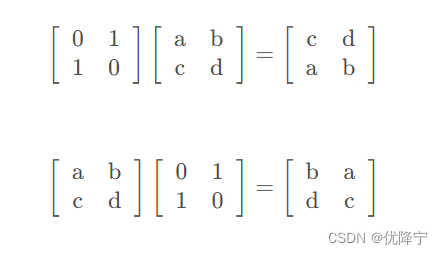
上述变换简称左行右列。左边是行变换比较容易理解的话,则转置之后就可以理解右边是列变换
逆矩阵
这里主要讨论消元矩阵的逆矩阵。消元矩阵之逆矩阵的实施效果就是抵消原矩阵的校园操作。消元矩阵实现了原矩阵A的操作,使第二行行向量[3,8,1]减掉了第一行的[1,2,1]的三倍变为[0,2,-2],则逆向操作就应该是把现在的第二行行向量[0,2,-2]加上第一行[1,2,1]的3倍,从而变回原来的第二行[3,8,1]。

