集合的自反关系和对称关系
集合的自反关系和对称关系
- 一:集合的自反关系
- 1:原理:
- 2:代码实现
- 二:对称关系
- 1:原理:
- 2:代码实现
- 三:总结
一:集合的自反关系
1:原理:
从给定的关系矩阵来断判关系R是否为自反是很容易的。若M(R的关系矩阵)的主对角线元素均为1,则R是自反关系;若M(R的关系矩阵)的主对角线元素均为0,则R是反自反关系;若M(R的关系矩阵)的主对角线元素既有1又有0,则R既不是自反关系也不是反自反关系。
2:代码实现
#include <stdio.h>
//判断自反关系
int fun1(int R[][4]) {for (int i = 0; i < 4; i++) {if (R[i][i] != 1) {return 0;}}return 1;
}
//判断反自反关系
int fun2(int R[][4]) {for (int i = 0; i < 4; i++) {if (R[i][i] != 0) {return 0;}}return 1;}#include <stdio.h>
//判断自反关系
int fun1(int R[][4]) {for (int i = 0; i < 4; i++) {if (R[i][i] != 1) {return 0;}}return 1;
}
//判断反自反关系
int fun2(int R[][4]) {for (int i = 0; i < 4; i++) {if (R[i][i] != 0) {return 0;}}return 1;二:对称关系
1:原理:
若M(R的关系矩阵)为对称矩阵,则R是对称关系;若M为反对称矩阵,则R是反对称关系。
2:代码实现
//判断对称关系
int fun3(int R[][4]) {for (int i = 0; i < 4; i++) {for (int j = 0; j < 4; j++) {if (R[i][j] != R[j][i]) {return 0;}}}return 1;
}
//判断反对称关系
int fun4(int R[][4]) {for (int i = 0; i < 4; i++) {for (int j = 0; j < 4; j++) {if (R[i][j] == 1 && R[j][i] == 1 && i != j) {return 0;}}}return 1;
}
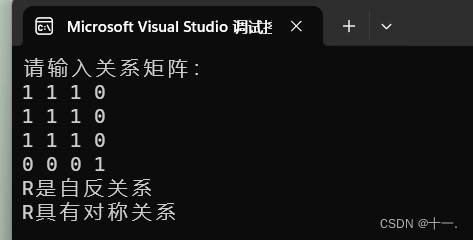
int main() {int R[4][4] = { 0 };printf("请输入关系矩阵:\n");for (int i = 0; i < 4; i++) {for (int j = 0; j < 4; j++) {scanf("%d", &R[i][j]);}}if ((fun1(R) + fun2(R))==0) {printf("R既不是自反关系也不是反自反关系\n");}if (fun3(R)) {printf("R具有对称关系\n");}if (fun4(R)) {printf("R具有反对称关系\n");}if (fun3(R) + fun4(R) == 2) {printf("R既具有对称关系又具有反对称关系\n");}if (fun3(R) + fun4(R) == 0) {printf("R既不具有对称关系又不具有反对称关系\n");}return 0;
}
三:总结
#include <stdio.h>
//判断自反关系
int fun1(int R[][4]) {for (int i = 0; i < 4; i++) {if (R[i][i] != 1) {return 0;}}return 1;
}
//判断反自反关系
int fun2(int R[][4]) {for (int i = 0; i < 4; i++) {if (R[i][i] != 0) {return 0;}}return 1;
}
//判断对称关系
int fun3(int R[][4]) {for (int i = 0; i < 4; i++) {for (int j = 0; j < 4; j++) {if (R[i][j] != R[j][i]) {return 0;}}}return 1;
}
//判断反对称关系
int fun4(int R[][4]) {for (int i = 0; i < 4; i++) {for (int j = 0; j < 4; j++) {if (R[i][j] == 1 && R[j][i] == 1 && i != j) {return 0;}}}return 1;
}
int main() {int R[4][4] = { 0 };printf("请输入关系矩阵:\n");for (int i = 0; i < 4; i++) {for (int j = 0; j < 4; j++) {scanf("%d", &R[i][j]);}}if (fun1(R)) {printf("R是自反关系\n");}if (fun2(R)) {printf("R是反自反关系\n");}if ((fun1(R) + fun2(R))==0) {printf("R既不是自反关系也不是反自反关系\n");}if (fun3(R)) {printf("R具有对称关系\n");}if (fun4(R)) {printf("R具有反对称关系\n");}if (fun3(R) + fun4(R) == 2) {printf("R既具有对称关系又具有反对称关系\n");}if (fun3(R) + fun4(R) == 0) {printf("R既不具有对称关系又不具有反对称关系\n");}return 0;
}