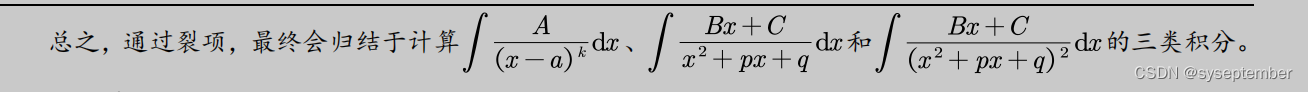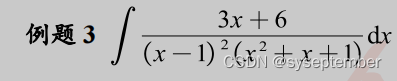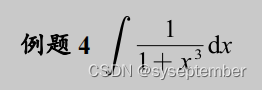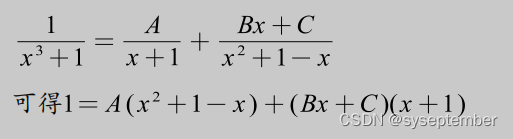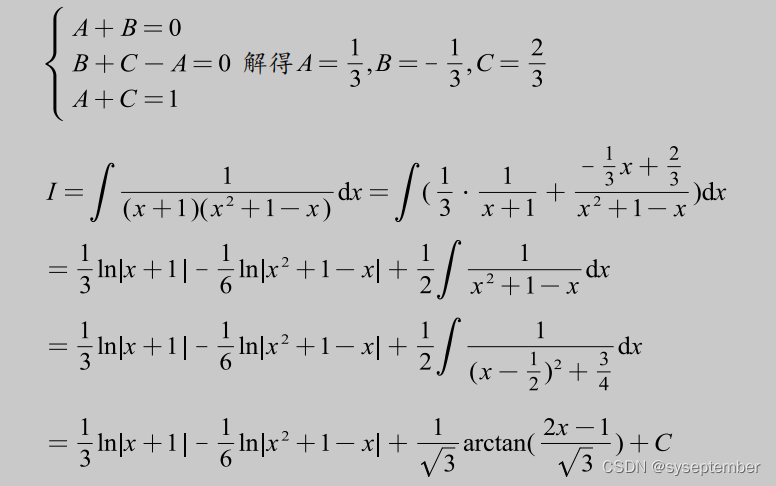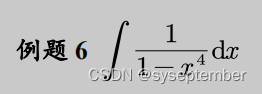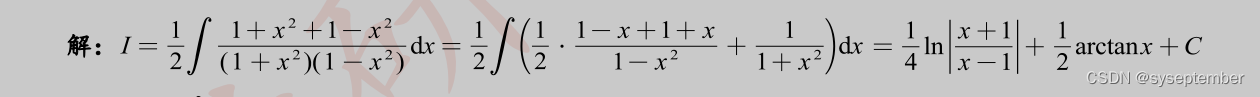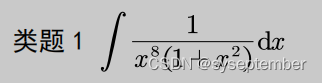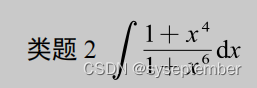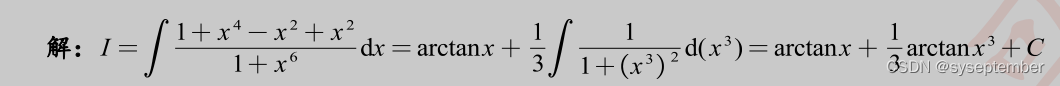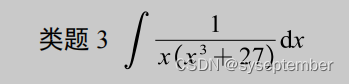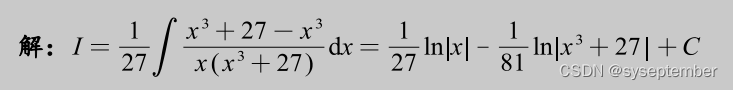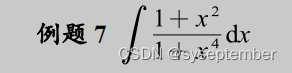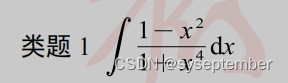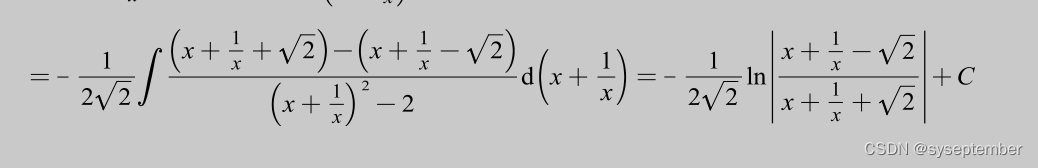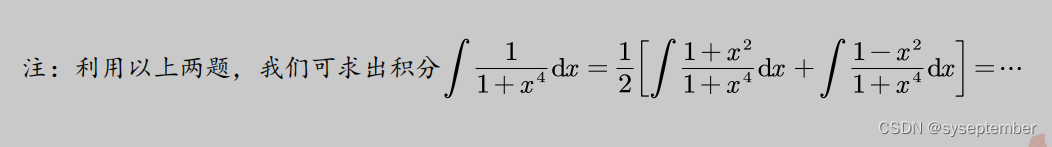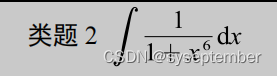【高数】不定积分之有理函数的积分
文章目录
- 前言
- 有理函数积分的通用解法
- 有理函数的特殊解法
前言
这个专栏开始更新高等数学的解题方法,本专栏没有特别强调概念,主要是让大家熟悉考研中的一些题型以及如何求解
关键步骤用蓝色高亮提示
总结方法用红色高亮提示
注意事项用绿色高亮提示
希望大家多多点赞,多多支持 ✨ ✨ ✨
有理函数积分的通用解法
当遇到题目是有理函数的积分时,我们一般采用有理函数积分的标准解法——“裂项+待定系数法”,对于某些特定有理函数的积分,也许有更加“巧妙”的方法,我们后面的例题也会涉及;但是希望大家不要过于追求这种巧妙的解法,还是应当以基本方法为主;
简要总结如下——我们将有理函数从宏观上分为真分式和假分式,而任何一个假分式都可以通过多项式的除法变成多项式与真分式之和,由于多项式的积分是简单的,所以解决有理函数的积分,本质上就变成了解决有理真分式的积分。 而对于真分式的积分,我们有如下固定套路
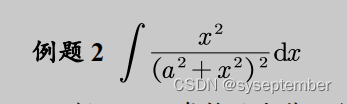
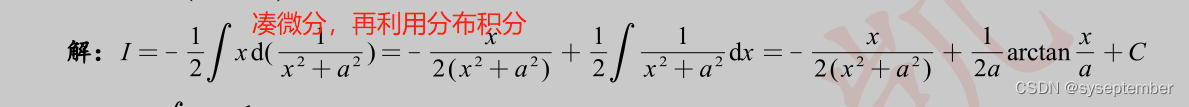
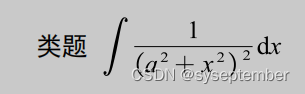




有理函数的特殊解法
从理论上而言,一切有理函数积分都可以用上面的待定系数法去硬肛,但是,通法不一定是最优解法,待定系数法的工作量往往很大。很多有理函数的积分都有着自己独特的解法,这些解法不能一概而论,需要我们仔细分析被积函数的结构,具体问题具体分析。大家一定要记住,学数学是一个“积累的过程,下面的很多解法都比较灵活,但希望大家不要产生畏难情绪。
注:我们在进行有理函数积分时,有时候会根据分母的形式,去改造分子同样可以实现“裂项”的目的。类似的题目还有以下几道