当前位置：首页 > news >正文

模型解释性：PFI、PDP、ICE等包的用法

news 2025/7/19 5:32:27

本篇主要介绍几种其他较常用的模型解释性方法。

1. Permutation Feature Importance(PFI)

1.1 算法原理

置换特征重要性(Permutation Feature Importance)的概念很简单，其衡量特征重要性的方法如下：计算特征改变后模型预测误差的增加。如果打乱该特征的值增加了模型的误差，那么一个特征就是重要的；如果打乱之后模型误差不变，那就认为该特征不重要。

1.2 Python实现

使用Wine酒数据来训练模型。其模型训练代码如下：

import pandas as pd
import numpy as np
from sklearn.datasets import load_wine
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
from matplotlib import pyplot as plt
import seaborn as snswine=load_wine()
X=pd.DataFrame(wine.data,columns=wine.feature_names)
y=wine.targetrfc=RandomForestClassifier(max_depth=4,random_state=0)
rfc.fit(X,y)
y_pred=rfc.predict(X)accuracy=accuracy_score(y,y_pred)

1.2.1 sklearn包实现

&ems;常用的机器学习包sklearn中也集成了这种方法，但是需要单独写代码来实现可视化。其具体代码如下：

from sklearn.inspection import permutation_importance
result=permutation_importance(rfc,X,y,n_repeats=10,random_state=42)feat=pd.DataFrame(np.hstack(([[col] for col in wine.feature_names],[[item] for item in result['importances_mean']])),columns=['Feat','Imp'])
feat['Imp']=feat['Imp'].astype(float)
feat=feat.sort_values('Imp',ascending=False)
sns.barplot(x='Imp',y='Feat',data=feat)
plt.show()

其结果如下：
在这里插入图片描述

1.2.2 eli5包实现

import eli5
from eli5.sklearn import PermutationImportance
perm=PermutationImportance(rfc,n_iter=10)
perm.fit(X,y)
eli5.show_weights(perm,feature_names=wine.feature_names)

其结果如下：
在这里插入图片描述

1.3 参考资料

https://blog.csdn.net/weixin_39653948/article/details/110731460
https://blog.csdn.net/qq_41185868/article/details/126046956

2 Partial Dependency Plots(部分依赖图,PDP)

2.1 算法原理

部分依赖图(PDP)展示了一个或两个特征对机器学习模型预测结果的边际效应。部分依赖图可以显示目标和特征之间的关系是线性的、单调的还是更复杂的关系。PDP假设所有特征两两不相关。其具体步骤如下：

训练一个机器学习模型(假设特征依次为 $F1…Fn,yF_{1} \dots F_{n},y$ 为目标变量);
假设需要探究特征 $F_{1}$ 对目标变量 $y$ 的边际效应;
特征 $F_{1}$ 的取值依次为 $(a1,a2,…,an)(a_{1},a_{2},\dots,a_{n})$ ; 依次用 $a1,a2,…,ana_{1},a_{2},\dots,a_{n}$ 代替 $F_{1}$ 列，其他特征保持不变。利用训练好的模型对这些数据进行预测，计算所有样本的预测平均值。
以特征 $F_{1}$ 的不同取值为X轴，其对应的预测样本平均值为Y轴进行作图即可。

2.2 Python实现

2.2.1 安装PDPbox包

使用如下代码直接安装PDPbox包的时候经常报错。报错的原因在于matplotlib V3.1.1无法正确安装。

pip install PDPbox

在网上查了很多资料也没有解决，所以在相关网站：https://pypi.tuna.tsinghua.edu.cn/simple/pdpbox/ 直接下载了pdpbox的压缩包，解压之后将以下两个文件直接放到python安装路径的lib/site-packages文件夹下即可。
在这里插入图片描述

2.2.2 PDPbox实现

单变量的边际效用

from pdpbox import pdppdp_goals=pdp.pdp_isolate(model=rfc,dataset=X,model_features=wine.feature_names,feature=wine.feature_names[0])
pdp.pdp_plot(pdp_goals,wine.feature_names[0])
plt.show()

在这里插入图片描述

交叉特征的边际效用

pdp_goals=pdp.pdp_interact(model=rfc,dataset=X,model_features=wine.feature_names,features=wine.feature_names[3:5])
pdp.pdp_interact_plot(pdp_goals,feature_names=wine.feature_names[3:5])
plt.show()

在这里插入图片描述

2.2.3 sklearn实现

除了使用专用的PDPbox箱之外，还可以使用sklearn包来实现部分依赖图。具体使用方法如下：

from sklearn.inspection import plot_partial_dependence
plot_partial_dependence(rfc,X,features=wine.feature_names[0:1],feature_names=wine.feature_names,target=0)
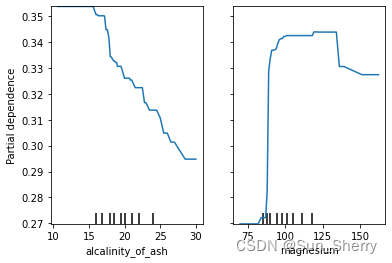
plt.show()plot_partial_dependence(rfc,X,features=wine.feature_names[3:5],feature_names=wine.feature_names,target=0)
plt.show()