1334. 阈值距离内邻居最少的城市
分析题目两点“阈值距离”、“邻居最少”。
“阈值距离”相当于定了个上界,求节点之间的最短距离。
“邻居最少”相当于能连接的点的数量。
求节点之间的最短距离有以下几种方法:
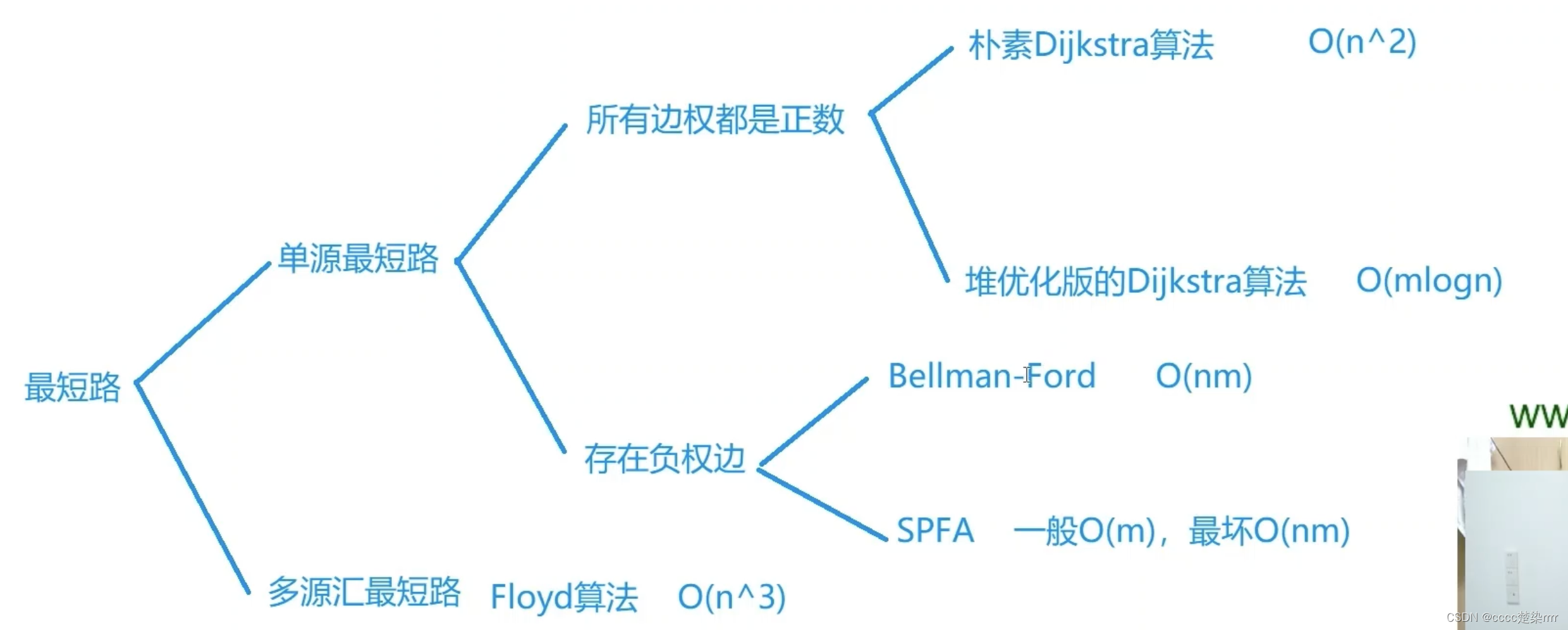
在这道题当中,n的范围是100以内,所以可以考虑O(n^3)的复杂度的算法
如果使用朴素Dijkstra算法,遍历所有点的算法复杂度为O(n*n^2)
如果使用堆优化版的Dijkstra算法,m=n^2,还不如朴素Dijkstra算法。
因此可以使用Floyd算法。
大致思路就是:先初始化一个最短距离矩阵d,然后每个节点一次遍历,对d值进行更新。
在这道题中,使用Floyd算法找到每个节点到其他节点的最短路径,然后遍历每个节点,找到在阈值距离内且可连接点数最少的节点。
class Solution {
public:int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {vector<vector<int>> d(n, vector<int>(n, 1e8)); // 这里的边值最大为1e4for (int i = 0; i < n; i++) d[i][i] = 0;for (auto v: edges) {int a = v[0], b = v[1], w = v[2];d[a][b] = d[b][a] = min(d[a][b], w); // 注意这里对边值的初始化要去最小值}for (int k = 0; k < n; k++) {for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {d[i][j] = min(d[i][j], d[i][k] + d[k][j]);}}}int res = -1, min_cnt = n + 1; // 初始下标和初始最小连接节点个数for (int i = 0; i < n; i++) {int cnt = 0;for (int j = 0; j < n; j++) {if (i != j && d[i][j] <= distanceThreshold) {cnt++;}}if (cnt <= min_cnt) {min_cnt = cnt;res = i;}}return res;}
};
