算法笔记-第七章-栈的应用(未完成)
算法笔记-第七章-栈的应用
- 栈的基本常识
- 栈的解释一
- 栈的解释二
- 栈的操作序列
- 合法的出栈序列
- 可能的出栈序列
- 补充知识点
- 后缀表达式(无优先级)
栈的基本常识
栈(Stack)是只允许在一端进行插入或删除操作的线性表。
栈的解释一
栈的解释二
栈的操作序列
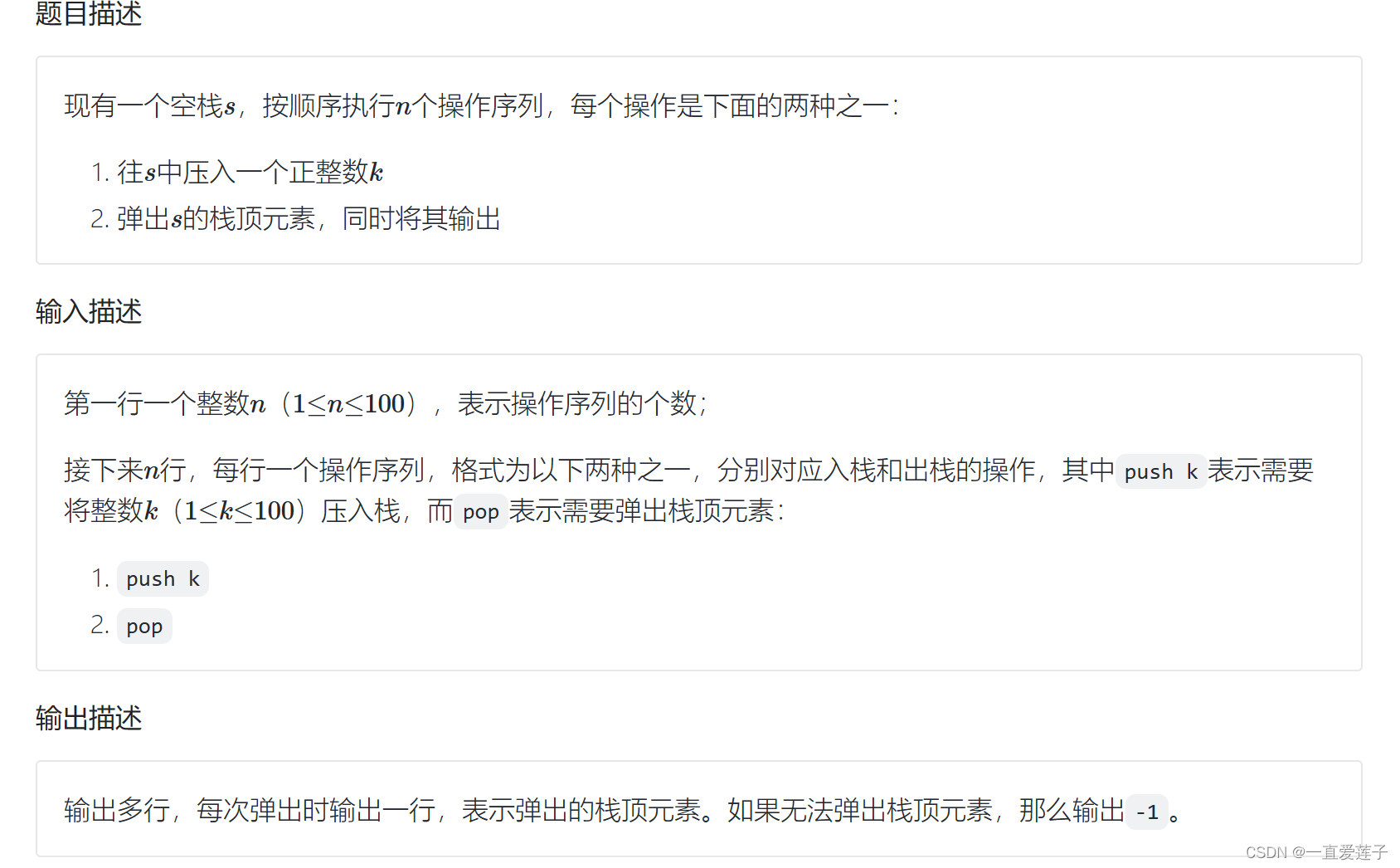
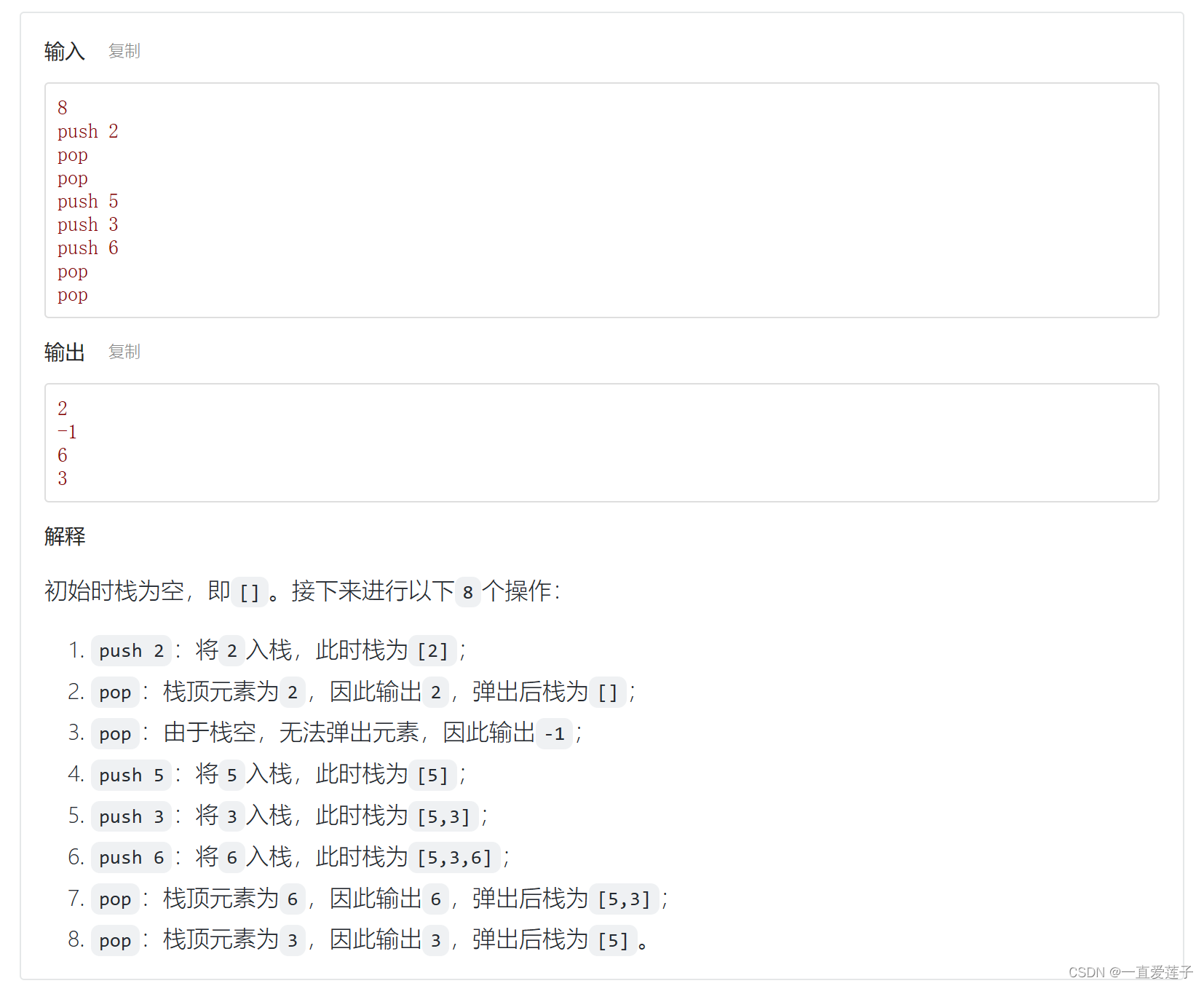
//栈的压入和输出
#include<iostream>
#include<stack>
#include<string>
using namespace std;
int main()
{int n, x;string action;//字符串的定义cin >> n;stack<int> s;//栈sfor (int i = 0; i < n; i++){cin >> action;if (action == "push")//如果输入的是push则压入栈中{cin >> x;s.push(x);}else {if (s.empty()) {cout <<-1 << endl; }else {cout << s.top() << endl; s.pop(); }}}return 0; }
合法的出栈序列
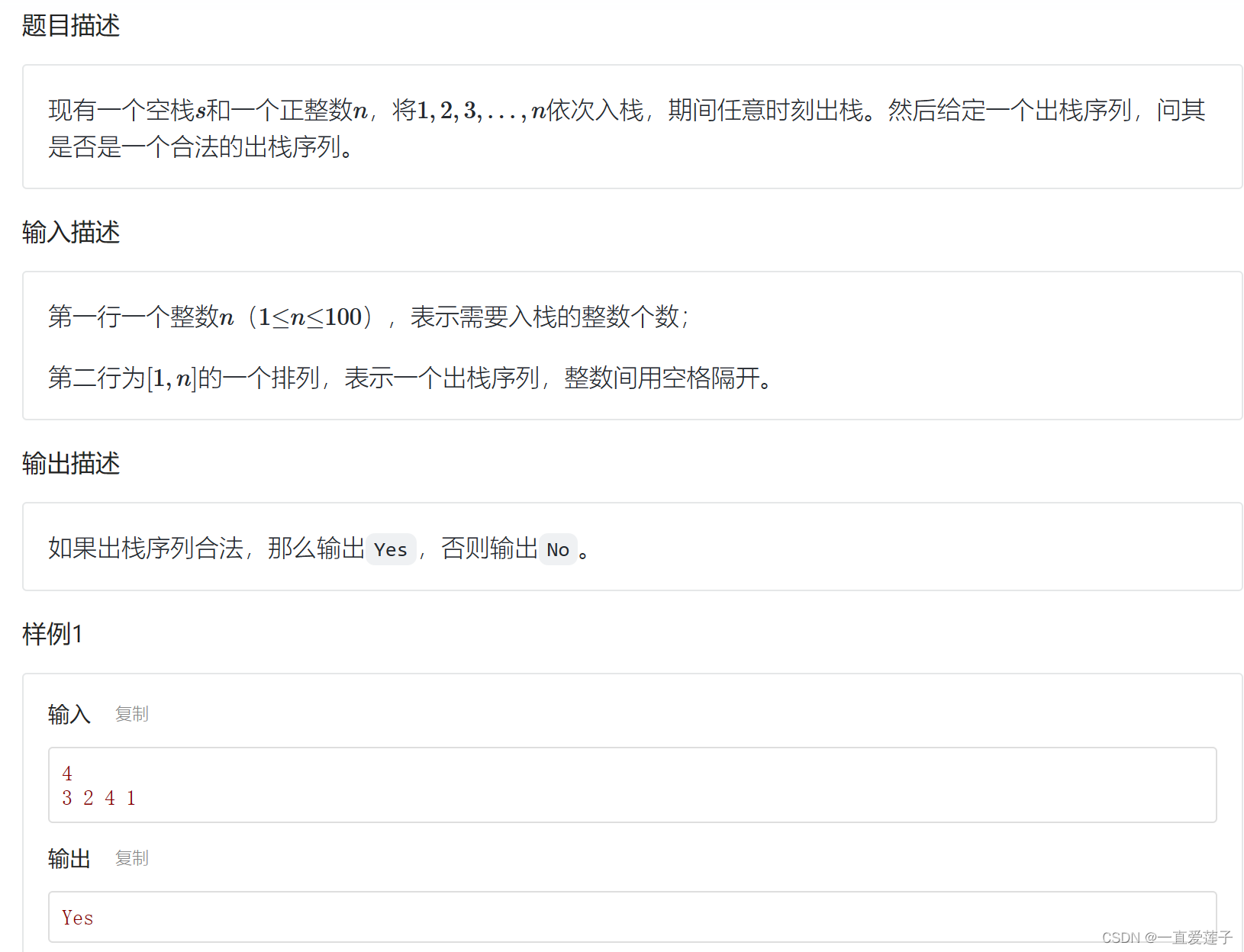
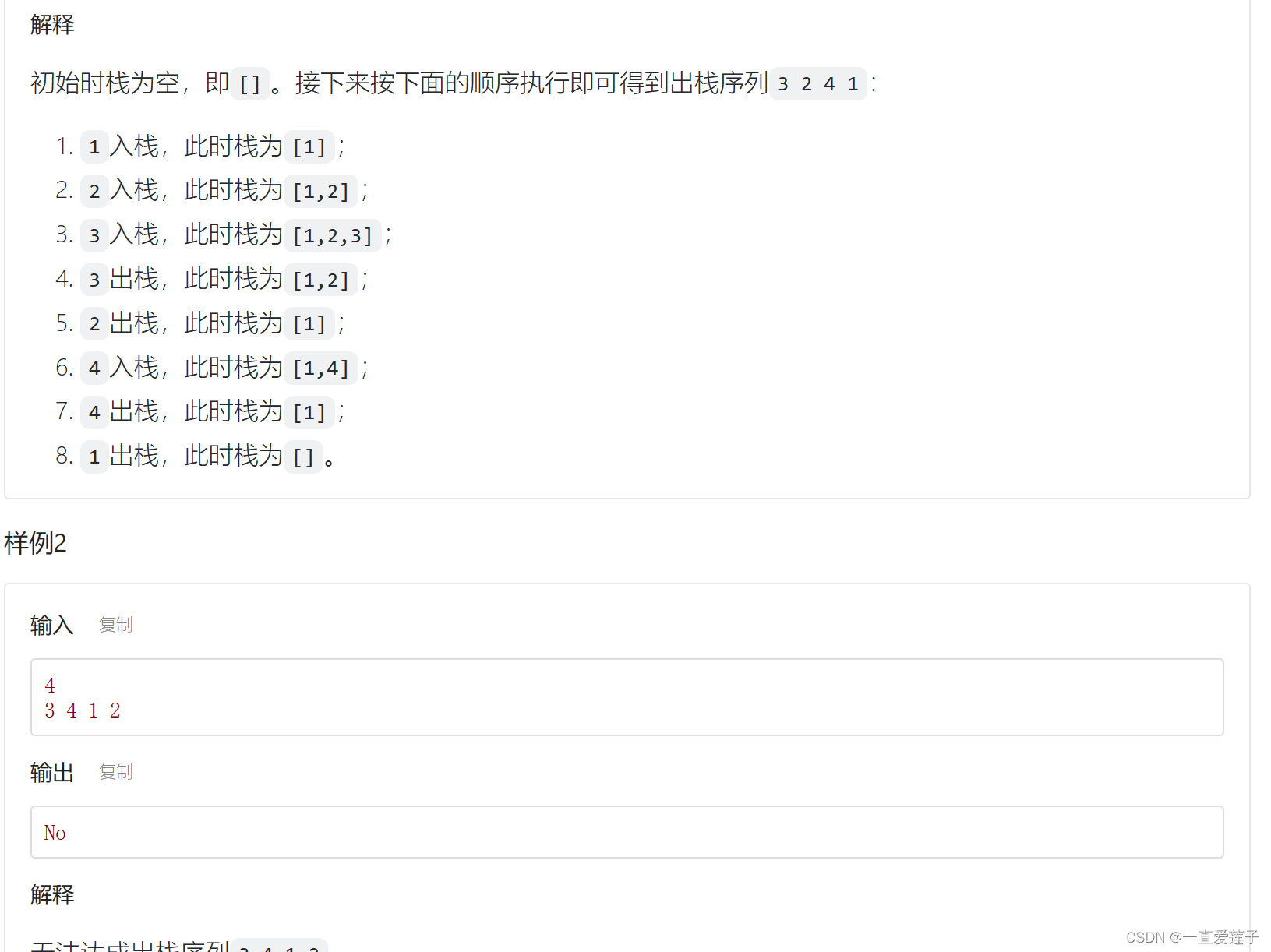
//合法的出栈序列#include <cstdio>
#include <stack>
using namespace std;int main()
{int n;scanf("%d", &n);stack<int> s;//栈int x, nowMax = 0;bool isValid = true;//布尔函数//已知:在入栈的时候任意 时刻都可以出栈,所以判断的条件为://是否为合理出栈序列:在出栈的时候是否序列是合理的//如果合理则出栈,否则直接就是false(直接布尔函数判定为No)for (int i = 0; i < n; i++) {scanf("%d", &x);if (x > nowMax) {for (int j = nowMax + 1; j <= x; j++) {s.push(j);}nowMax = x;}if (s.top() != x) {isValid = false; break; }else {s.pop(); }}printf(isValid ? "Yes" : "No"); return 0;
}
可能的出栈序列
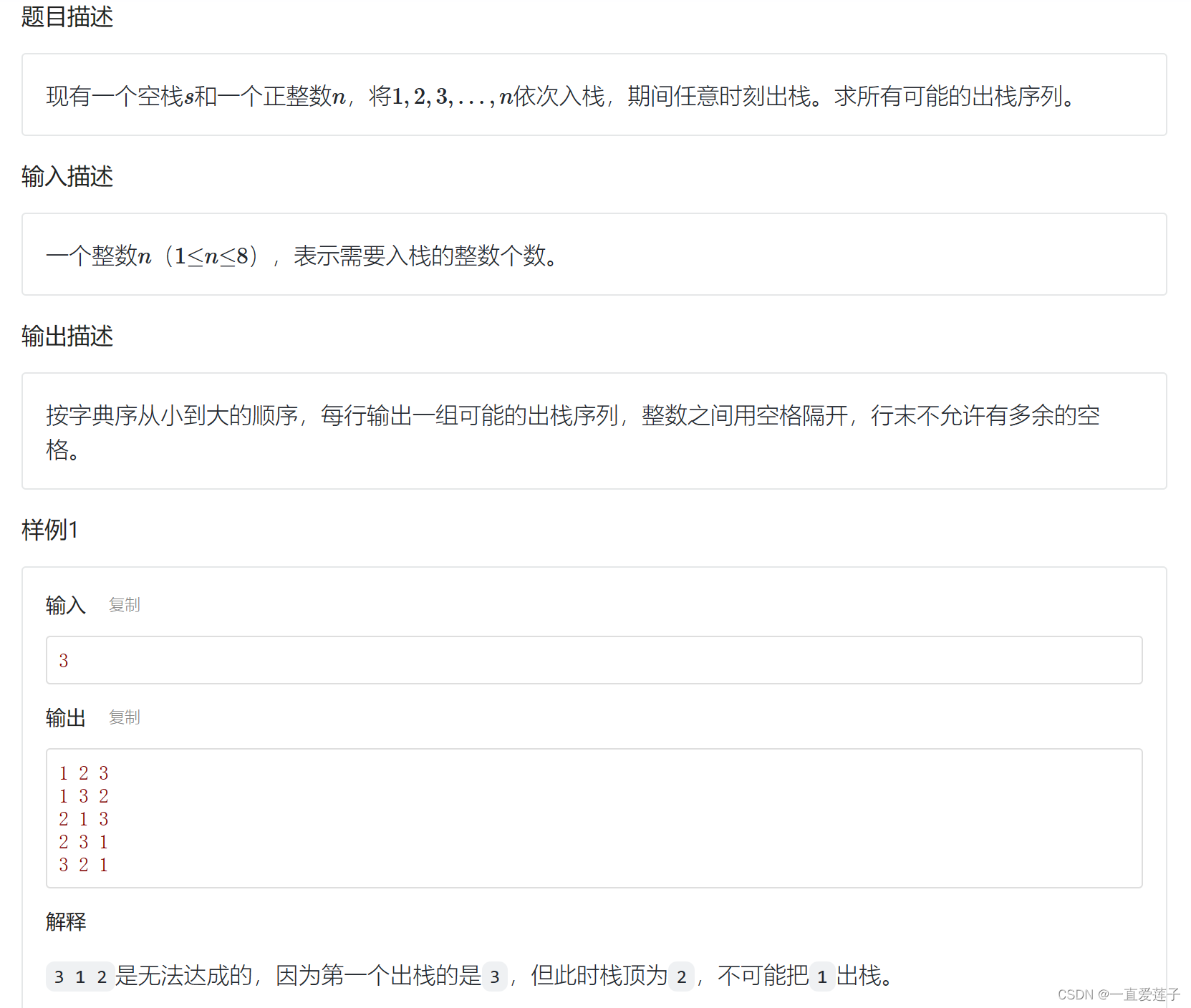
补充知识点
一:C++用vector来表示二维数组;必须先将vector定义为二维数组:vector A
二:定义
vector<vector<int> >a(n);
初始化一个n*m的二维数组
for (int i = 0; i < n; i++)
{a[i].resize(m);
}二:赋值操作
//现在像二维数组那样赋值即可;
for(int i=0;i<m;i++) {for(int j=0;j<n;j++) {a[i][j] = (3*i+j+1); }}(抄录)-两个矩阵之和
//计算两个二维数组之和
#include <iostream>
#include <vector>
#include<cmath>
using namespace std;
vector<vector<int> > sum(vector<vector<int> > b, vector<vector<int> > c)
{//此处同样需要先将a定义为二维数组结构; vector<vector<int> > a(4);for (int i = 0; i < 4; i++){a[i].resize(3);}// vector<int> a2;for (int i = 0; i < b.size(); i++){for (int j = 0; j < b[i].size(); j++){a[i][j] = b[i][j] + c[i][j];}}return a;
}int main()
{//要先定义好二维数组结构,才能直接像二维数组一样赋值; 否则程序没办法往后面运行的; vector<vector<int> > b1(4);vector<vector<int> > c1(4);//不能直接写 vector<vector<int> > a1;需要初始化大小; vector<vector<int> > a1(4);for (int i = 0; i < 4; i++){b1[i].resize(3);}for (int i = 0; i < 4; i++){c1[i].resize(3);}for (int i = 0; i < 4; i++){a1[i].resize(3);}//vector<vector<int> >赋值: for (int i = 0; i < 4; i++){for (int j = 0; j < 3; j++){b1[i][j] = (3 * i + j + 1);}}for (int i = 0; i < 4; i++){for (int j = 0; j < 3; j++){c1[i][j] = 3 * i + j + 1;}}//显示vector<vector<int> >; printf("Array b1: \n");for (int i = 0; i < 4; i++){for (int j = 0; j < 3; j++){printf("b1[%d][%d] = %d\t", i, j, b1[i][j]);}cout << endl;}printf("Array c1: \n");for (int i = 0; i < 4; i++){for (int j = 0; j < 3; j++){printf("c1[%d][%d] = %d\t", i, j, c1[i][j]);}cout << endl;}a1 = sum(b1, c1);printf("Array a1: \n");for (int i = 0; i < 4; i++){for (int j = 0; j < 3; j++){printf("a1[%d][%d] = %d\t", i, j, a1[i][j]); }cout << endl; }system("pause"); return 0;
}
后缀表达式(无优先级)
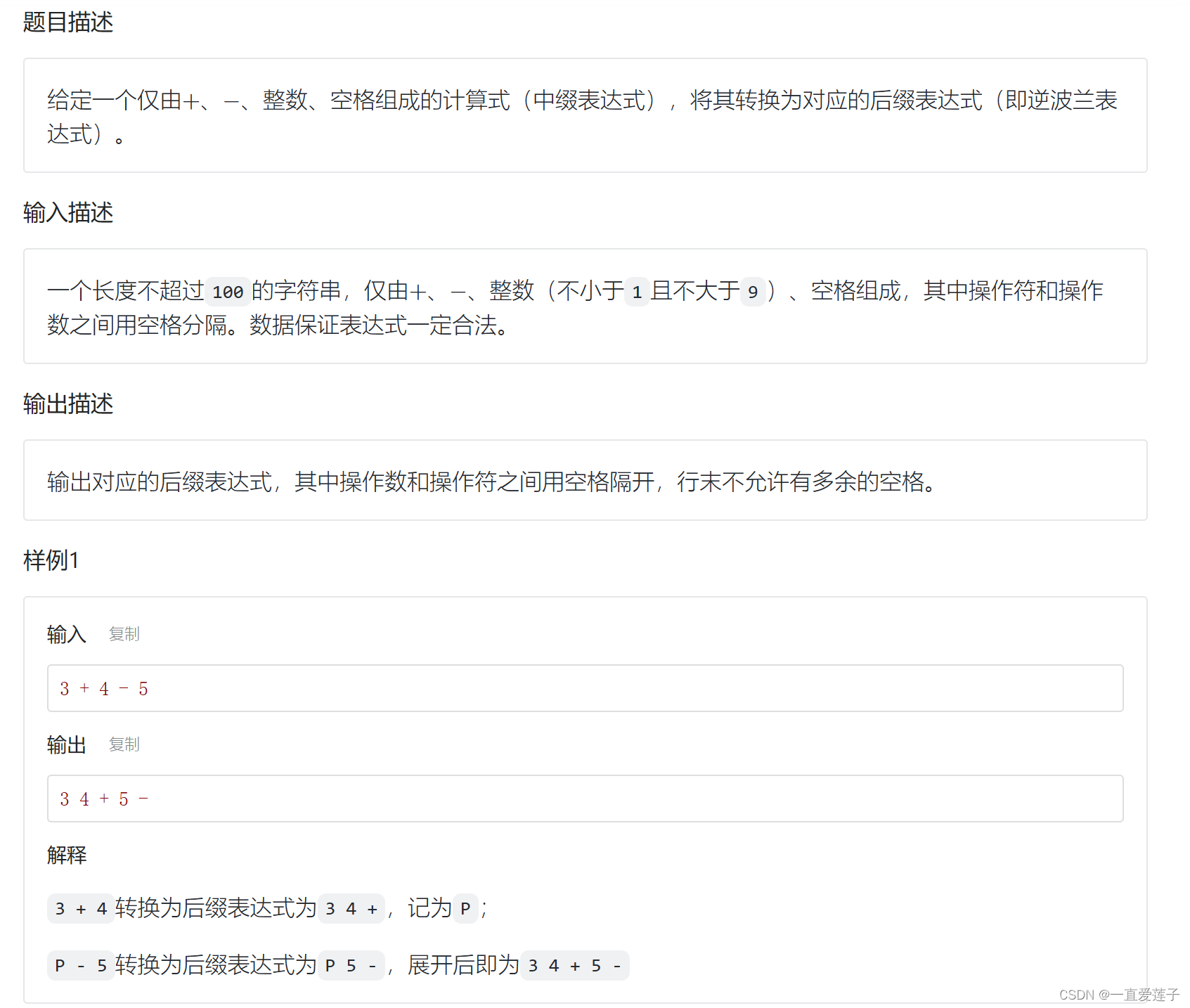
注意点:
答案是这样的:
#include <iostream>
#include <string>
using namespace std;string toPostfixExpr(string infixExpr) {string result = "";result += infixExpr[0];for (int i = 2; i < infixExpr.length(); i += 4) {result += " ";result += infixExpr[i + 2];result += " ";result += infixExpr[i];}return result;
}int main() {string expr;getline(cin, expr);cout << toPostfixExpr(expr);return 0;
}
但是我认为有一些问题**************************
正常的表达式子;
参考大佬讲解
中缀转换成后缀表达式
