【C语言数据结构————————二叉树】
文章目录
-
文章目录
-
一、什么是树
-
树的定义
-
树的种类
-
树的深度
-
树的基本术语
-
-
二、满二叉树
-
定义
-
满二叉树的特点
-
-
三、完全二叉树
-
定义
-
特点
-
-
四、二叉树的性质
-
五、二叉树的存储结构
-
顺序存储结构
-
链式存储结构
-
-
六、二叉树的基本操作
-
七、二叉树的创建
-
八、二叉树的遍历
-
前序遍历
-
中序遍历
-
后序遍历
-
-
九、二叉树的销毁
-
十、二叉树中节点的查找
欢迎阅读新一期的c语言数据结构模块————二叉树
✒️个人主页:-_Joker_-
🏷️专栏:C语言数据结构
📜代码仓库:c_code
🌹🌹欢迎大佬们的阅读和三连关注,顺着评论回访🌹🌹
一、什么是树
1.树的定义
树是n(n>=0)个结点的有限集。当n = 0时,称为空树。在任意一棵非空树中应满足:
- 有且仅有一个特定的称为根的结点。
- 当n>1时,其余节点可分为m(m>0)个互不相交的有限集T1,T2,…,Tm,其中每个集合本身又是一棵树,并且称为根的子树。
2.树的种类
树的种类可以分为以下几种
- 无序树:树中任意节点的子结点之间没有顺序关系,这种树称为无序树,也称为自由树;
- 有序树:树中任意节点的子结点之间有顺序关系,这种树称为有序树;
- 二叉树:每个节点最多含有两个子树的树称为二叉树;
- 满二叉树:叶节点除外的所有节点均含有两个子树的树被称为满二叉树;
- 完全二叉树:除最后一层外,所有层都是满节点,且最后一层缺右边连续节点的二叉树称为完全二叉树;
- 哈夫曼树(最优二叉树):带权路径最短的二叉树称为哈夫曼树或最优二叉树。
3.树的深度
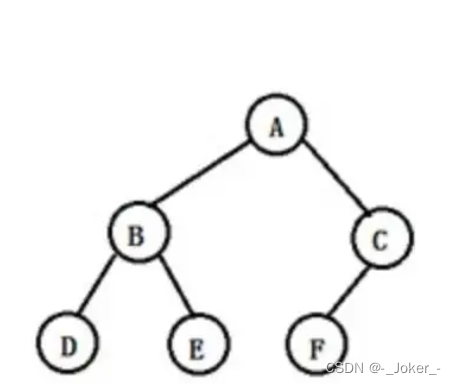
定义一棵树的根结点层次为1,其他结点的层次是其父节点层次加1。一棵树中所有结点的层次的最大值称为这棵树的深度。例如:
如图,图中的树的深度为:3
4.树的基本术语
- 结点的度:结点拥有的子树数目
- 叶子(终端)结点:度为0的结点
- 分支(非终端)结点:度不为0的结点
- 树的度:树的各结点度的最大值
- 内部结点:除根结点之外的分支结点
- 双亲与孩子结点:结点的子树的根称为该结点的孩子;该结点称为孩子的双亲
- 兄弟:属于同一双亲的孩子
- 结点的祖先:从根到该结点所经分支上的所有结点
- 结点的子孙:该结点为根的子树中的任一结点
- 结点的层次:表示该结点在树中的相对位置。根为第一层,其他的结点依次下推;若
- 结点在第L层上,则其孩子在第L+1层上
- 兄弟节点:双亲在同一层的结点互为兄弟节点
- 树的深(高)度:树中结点的最大层次
- 有序树:树中各结点的子树从左至右是有次序的,不能互换。否则,称为无序树
- 路径长度:从树中某结点Ni出发,能够“自上而下”通过树中结点到达结点Nj,则称Ni到Nj存在
- 一条路径,路径长度等于这两个结点之间的分支数
- 树的路径长度:从根到每个结点的路径长度之和。
- 森林:是m(m≥0)棵互不相交的树的集合
由于二叉树的使用在数据结构中更加广泛,所以我们以二叉树为主来进行讲解,下面介绍一下关于二叉树的基本知识。
二、满二叉树
定义:
二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子节点都在同一层上,这样的二叉树称为满二叉树。
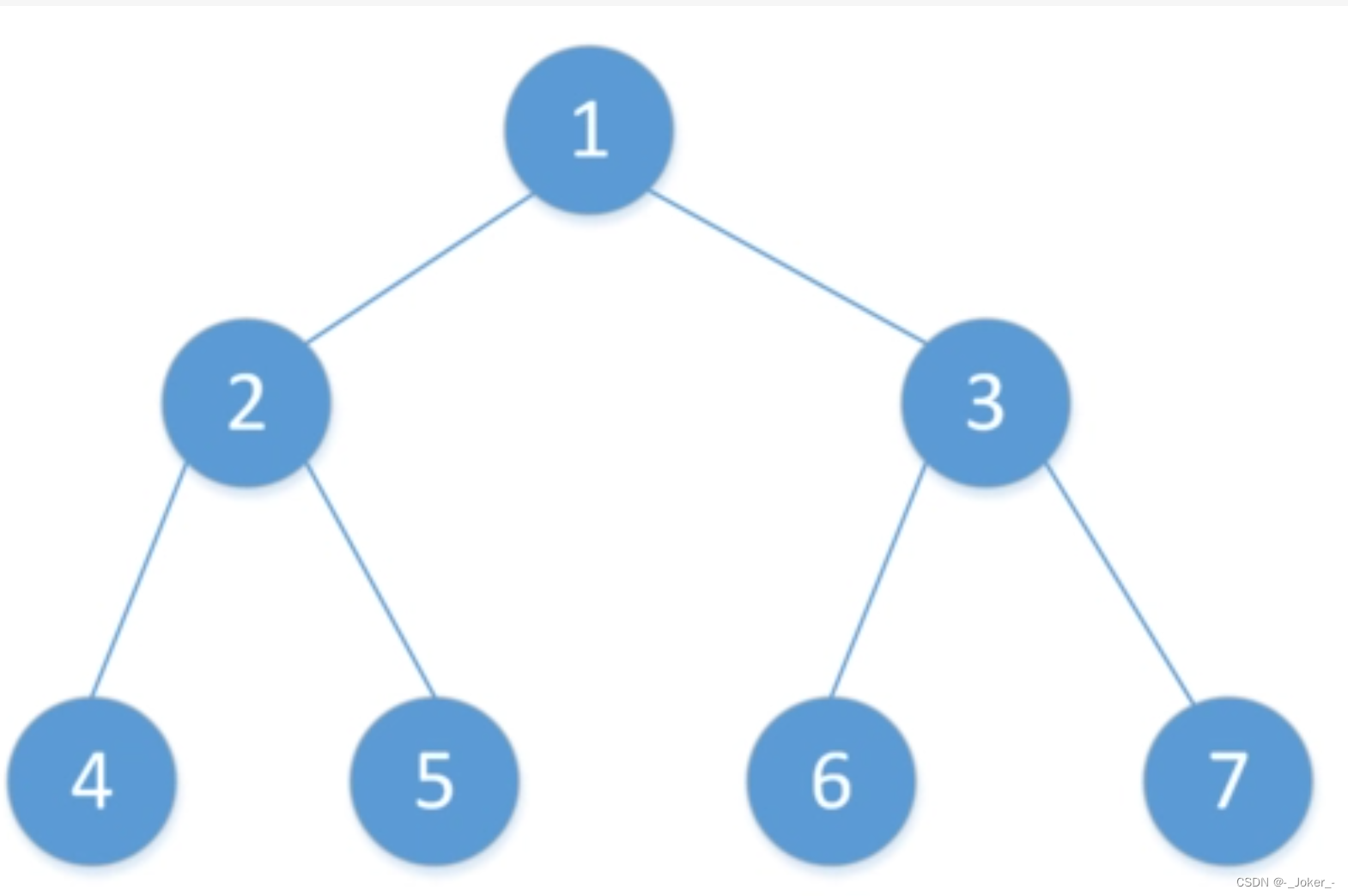
如图为一颗满二叉树
满二叉树的特点
满二叉树的特点有:
- 叶子节点只能出现在最下一层。
- 非叶子结点的度一定是2。
- 在同样深度的二叉树中,满二叉树的结点个数最多,叶子数最多。
- 设树的深度为i,则总结点数为 2^i -1
- 满二叉树是一种特殊的完全二叉树
- 若有双亲,则其双亲为i / 2,若有左孩子,则左孩子为2i ,若有右孩子,则右孩子为2i + 1 。
三、完全二叉树
定义
对二叉树节点由左至右由上至下的编号,如果编号为i的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这棵二叉树称为完全二叉树。
如图为一颗完全二叉树
特点
- 叶子结点只能出现在最下层和次下层。
- 最下层的叶子结点集中在树的左部。
- 倒数第二层若存在叶子结点,一定在右部连续位置。
- 如果结点度为1,则该结点只有左孩子,即没有右子树。
- 同样结点数目的二叉树,完全二叉树深度最小。
- 满二叉树一定是完全二叉树,但反过来不一定成立。
四、二叉树的性质
- 二叉树的第i层上至多有2^(i-1) (i≥1)个结点
- 深度为k的二叉树至多有2^k-1个结点(k≥1)
- 对任何一棵二叉树T,如果其终端结点数为N0,度为2的结点数为N2,则N0=N2+1
- 具有n个结点的完全二叉树的深度为[log2(n)]+1
- 一棵具有n个结点的完全二叉树(又称顺序二叉树)对其结点按层从上至下(每层从左至右)进行1-n的编号,则对任一结点i(1≤i≤n)有:
- 若i>1,则i的双亲是[i/2];若i=1,则i是根,无双亲。
- 若2i≤n,则i的左孩子是2i;否则,i无左孩子
- 若2i+1≤n,则i的右孩子是2i+1;否则,i无右孩子
五、二叉树的储存结构
二叉树的储存结构分为顺序存储结构和链式存储结构
顺序存储结构
二叉树的顺序存储是指用一组地址连续的存储单元依次自上而下、自左至右存储完全二叉树上的结点元素,即将完全二叉树上编号为i ii的结点元素存储在一维数组下标为 i − 1的分量中。
依据二叉树的性质,完全二叉树和满二叉树采用顺序存储比较合适,树中结点的序号可以唯一地反映结点之间的逻辑关系,这样既能最大可能地节省存储空间,又能利用数组元素的下标值确定结点在二叉树中的位置,以及结点之间的关系。
但对于一般的二叉树,为了让数组下标能反映二叉树中结点之间的逻辑关系,只能添加一些并不存在的空结点,让其每个结点与完全二叉树上的结点相对照,再存储到一维数组的相应分量中。然而,在最坏情况下,一个高度为h 且只有h 个结点的单支树却需要占据近2h-1个存储单元。二叉树的顺序存储结构如图所示,其中0表示并不存在的空结点。
链式存储结构
由于顺序储存结构非常不便,所以我们通常采用链式存储结构实现二叉树。链式存储结构通过开辟一块空间(节点),通过指针储存左孩子、右孩子节点以及数据。
由于顺序结构操作起来并不方便,所以我们通常都以链式存储结构通过递归来实现二叉树,定义如下
typedef struct BinaryTree
{int val;struct BinaryTree *left;struct BinaryTree *right;
}BT;六、二叉树的基本操作
- CreateTree() :创建二叉树
- PreOrder(BT* root):二叉树的前序遍历
- InOrder(BT* root): 二叉树的中序遍历
- BackOrder(BT* root): 二叉树的后序遍历
- DestoryTree(BT* root):销毁二叉树
- FindTree(BT* root, int x):查找二叉树中值为x的节点
七、二叉树的创建
如下是对二叉树进行创建的算法
BTNode* CreatNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");exit(-1);}node->val = x;node->left = NULL;node->right = NULL;return node;
}八、二叉树的遍历
前序遍历
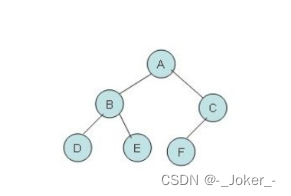
二叉树的前序遍历顺序为根 - 左 - 右
即先访问根节点
然后访问其左孩子节点
最后访问其右孩子节点
例如上图,前序遍历顺序为:A -> B -> D -> E -> C -> F
算法如下
void PreOrder(BT* root)
{if (root == NULL){return;}printf("%d",root->val);PreOrder(root->left);PreOrder(root->right);
}中序遍历
二叉树的前序遍历顺序为左 - 根 - 右
即先访问左孩子节点
然后访问其根节点
最后访问其右孩子节点
例如上图,前序遍历顺序为:D -> B -> E -> A -> F -> C
算法如下
void InOrder(BT* root)
{if (root == NULL){return;}InOrder(root->left);printf("%d ", root->val);InOrder(root->right);
}后序遍历
二叉树的前序遍历顺序为左 - 右 - 根
即先访问左孩子节点
然后访问其根节点
最后访问其右孩子节点
例如上图,前序遍历顺序为:D -> E -> B -> F -> C -> A
算法如下
void BackOrder(BT* root)
{if (root == NULL){return;}BackOrder(root->left);BackOrder(root->right);printf("%d ", root->val);
}九、二叉树的销毁
二叉树的销毁同样通过递归来实现:
void DestoryTree(BT* root)
{if (root == NULL){return;}DestoryTree(root->left);DestoryTree(root->right);free(root);
}
十、二叉树中节点的查找
BT* FindTree(BT* root, int x)
{if (root == NULL){return;}if (root->val == x)return root;FindTree(root->left, x);FindTree(root->right, x);return NULL;
}