第三章:人工智能深度学习教程-基础神经网络(第四节-从头开始的具有前向和反向传播的深度神经网络 – Python)
本文旨在从头开始实现深度神经网络。我们将实现一个深度神经网络,其中包含一个具有四个单元的隐藏层和一个输出层。实施将从头开始,并实施以下步骤。
算法:
1. 可视化输入数据
2. 确定权重和偏置矩阵的形状
3. 初始化矩阵、要使用的函数
4. 前向传播方法的实现
5. 实施成本计算
6. 反向传播和优化
7. 预测和可视化输出
模型架构:模型
架构如下图所示,其中隐藏层使用双曲正切作为激活函数,而输出层(即分类问题)使用 sigmoid 函数。

模型架构
权重和偏差:
首先必须声明两个层将使用的权重和偏差,并且其中的权重将随机声明,以避免所有单元的输出相同,而偏差将初始化为零。计算将从头开始并根据下面给出的规则进行,其中 W1、W2 和 b1、b2 分别是第一层和第二层的权重和偏差。这里A代表特定层的激活。
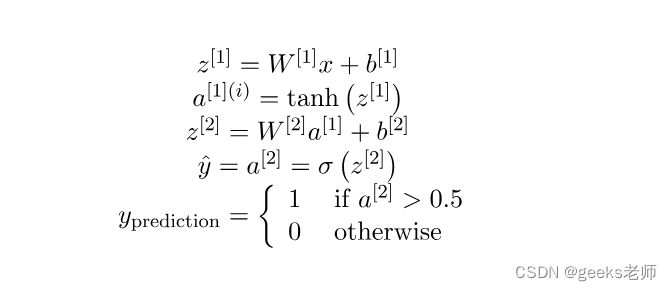
成本函数:
上述模型的成本函数将属于逻辑回归所使用的成本函数。因此,在本教程中我们将使用成本函数:
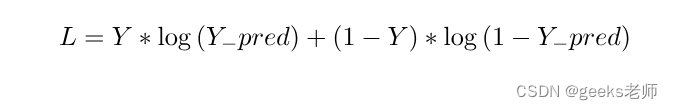
代码:可视化数据
# 导入包
import numpy as np
import matplotlib.pyplot as plt# 从 planar_utils.py 的 GitHub 仓库中导入所需函数和数据集
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset# 加载示例数据
X, Y = load_planar_dataset()# 可视化数据
plt.scatter(X[0, :], X[1, :], c=Y, s=40, cmap=plt.cm.Spectral)
这段代码执行以下操作:
- 导入了NumPy库和Matplotlib库,用于数值计算和数据可视化。
- 从
planar_utils.py的GitHub仓库中导入了一些自定义函数和示例数据集,包括plot_decision_boundary、sigmoid和load_planar_dataset。- 使用
load_planar_dataset函数加载了示例数据集,其中X是特征矩阵,Y是目标标签。- 使用
plt.scatter函数可视化了数据集,将数据点根据目标标签Y的值着色,使用不同的颜色展示不同类别的数据点。这段代码用于加载示例数据集并可视化数据,以便了解数据的分布和结构。
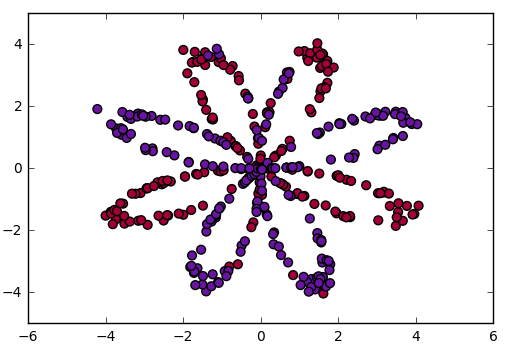
代码:初始化权重和偏差矩阵
这里隐藏单元的数量为4,因此,W1权重矩阵的形状为(4,特征数),偏差矩阵的形状为(4, 1),广播后根据上面的公式相加得到权重矩阵。同样的情况也适用于W2。
# X --> 输入数据集的形状 (输入大小, 样本数量)
# Y --> 标签的形状 (输出大小, 样本数量)# 初始化第一层权重和偏置
W1 = np.random.randn(4, X.shape[0]) * 0.01
b1 = np.zeros(shape=(4, 1))# 初始化第二层权重和偏置
W2 = np.random.randn(Y.shape[0], 4) * 0.01
b2 = np.zeros(shape=(Y.shape[0], 1))这段代码执行以下操作:
初始化了第一层权重
W1和偏置b1,这是一个神经网络的隐藏层。W1的形状为 (4, 输入大小),b1的形状为 (4, 1)。这些参数通常需要根据网络结构和问题进行初始化。初始化了第二层权重
W2和偏置b2,这是神经网络的输出层。W2的形状为 (输出大小, 4),b2的形状为 (输出大小, 1)。这些参数也需要根据网络结构和问题进行初始化。这些初始化的参数用于构建神经网络模型,并在训练过程中进行调整以适应数据。通常,它们的初始化值是小的随机值,以帮助网络在训练中学习有效的表示。
代码:前向传播:
现在我们将使用 W1、W2 和偏差 b1、b2 执行前向传播。在此步骤中,在定义为forward_prop的函数中计算相应的输出。
# X --> 输入数据集的形状 (输入大小, 样本数量)
# Y --> 标签的形状 (输出大小, 样本数量)# 初始化第一层权重和偏置
W1 = np.random.randn(4, X.shape[0]) * 0.01
b1 = np.zeros(shape=(4, 1))# 初始化第二层权重和偏置
W2 = np.random.randn(Y.shape[0], 4) * 0.01
b2 = np.zeros(shape=(Y.shape[0], 1))
这段代码执行以下操作:
初始化了第一层权重
W1和偏置b1,这是一个神经网络的隐藏层。W1的形状为 (4, 输入大小),b1的形状为 (4, 1)。这些参数通常需要根据网络结构和问题进行初始化。初始化了第二层权重
W2和偏置b2,这是神经网络的输出层。W2的形状为 (输出大小, 4),b2的形状为 (输出大小, 1)。这些参数也需要根据网络结构和问题进行初始化。这些初始化的参数用于构建神经网络模型,并在训练过程中进行调整以适应数据。通常,它们的初始化值是小的随机值,以帮助网络在训练中学习有效的表示。
代码:定义成本函数:
# 这里 Y 是实际输出
def 计算成本(A2, Y):m = Y.shape[1]# 实现上述公式成本总和 = np.multiply(np.log(A2), Y) + np.multiply((1 - Y), np.log(1 - A2))成本 = -np.sum(成本总和) / m# 压缩以避免不必要的维度成本 = np.squeeze(成本)return 成本
这段代码定义了一个函数,用于计算模型的成本。函数的输入参数包括模型的预测输出
A2和实际目标值Y。它使用交叉熵损失函数来计算成本。成本是根据模型的预测和实际目标值计算得出的,以衡量模型的性能。最后,通过np.squeeze压缩成本以避免不必要的维度。这个函数用于在训练神经网络时评估模型的性能,并根据成本来调整模型的参数以最小化损失。
代码:最后是反向传播函数:
这是非常关键的一步,因为它涉及大量线性代数来实现深度神经网络的反向传播。求导数的公式可以用线性代数的一些数学概念来推导,我们在这里不打算推导。请记住,dZ、dW、db 是成本函数关于各层的加权和、权重、偏差的导数。
def 反向传播(W1, b1, W2, b2, cache): # 从字典 "cache" 中获取 A1 和 A2A1 = cache['A1'] A2 = cache['A2'] # 反向传播:计算 dW1、db1、dW2 和 db2dZ2 = A2 - Y dW2 = (1 / m) * np.dot(dZ2, A1.T) db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True) dZ1 = np.multiply(np.dot(W2.T, dZ2), 1 - np.power(A1, 2)) dW1 = (1 / m) * np.dot(dZ1, X.T) db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True) # 根据算法更新参数W1 = W1 - 学习率 * dW1 b1 = b1 - 学习率 * db1 W2 = W2 - 学习率 * dW2 b2 = b2 - 学习率 * db2 return W1, W2, b1, b2
这段代码实现了神经网络的反向传播算法,根据损失函数的梯度来更新模型的参数。反向传播用于训练神经网络,通过计算梯度并根据学习率来更新权重和偏置,以最小化成本函数。这个函数返回更新后的参数
W1、W2、b1和b2。
代码:训练自定义模型现在我们将使用上面定义的函数来训练模型,可以根据处理单元的便利性和功能来放置历元。
# 请注意,权重和偏置是全局的
# 这里的 num_iterations 对应训练的周期数(epochs)
for i in range(0, num_iterations): # 正向传播。输入: "X, parameters",返回: "A2, cache"。A2, cache = forward_propagation(X, W1, W2, b1, b2) # 成本函数。输入: "A2, Y"。输出: "cost"。cost = compute_cost(A2, Y) # 反向传播。输入: "parameters, cache, X, Y"。输出: "grads"。W1, W2, b1, b2 = backward_propagation(W1, b1, W2, b2, cache) # 每隔 1000 次迭代打印成本if print_cost and i % 1000 == 0: print ("第 %i 次迭代后的成本: %f" % (i, cost))
这段代码执行以下操作:
通过循环(
for i in range(0, num_iterations)),进行多个训练周期(epochs)的迭代。在每个训练周期中,模型将数据进行正向传播(forward_propagation)、计算成本(compute_cost)并进行反向传播(backward_propagation)来更新参数。正向传播计算模型的预测输出
A2和缓存信息cache。成本函数计算模型的成本,用于评估模型的性能。
反向传播计算参数的梯度,然后使用梯度下降算法来更新权重和偏置。
如果
print_cost为真并且迭代次数能被 1000 整除,将打印出当前迭代次数和成本值,以监控训练进度。这个代码段用于训练神经网络,以便模型可以逐渐优化,以拟合训练数据并获得更好的性能。
使用学习参数进行
输出训练模型后,使用上面的forward_propagate函数获取权重并预测结果,然后使用这些值绘制输出图。您将得到类似的输出。
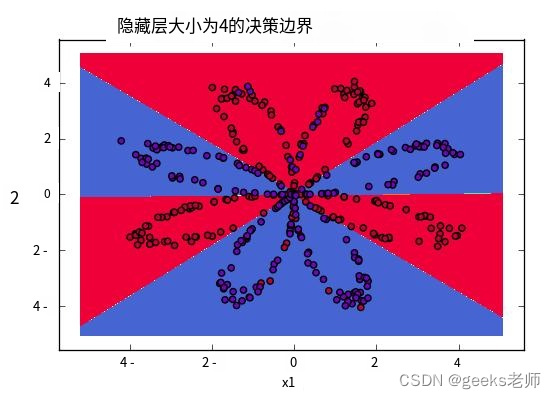
可视化数据边界
结论:
深度学习是一个掌握基础知识的人占据王座的世界,因此,尝试将基础知识发展得足够强大,以便之后,您可能成为新模型架构的开发人员,这可能会彻底改变社区。
