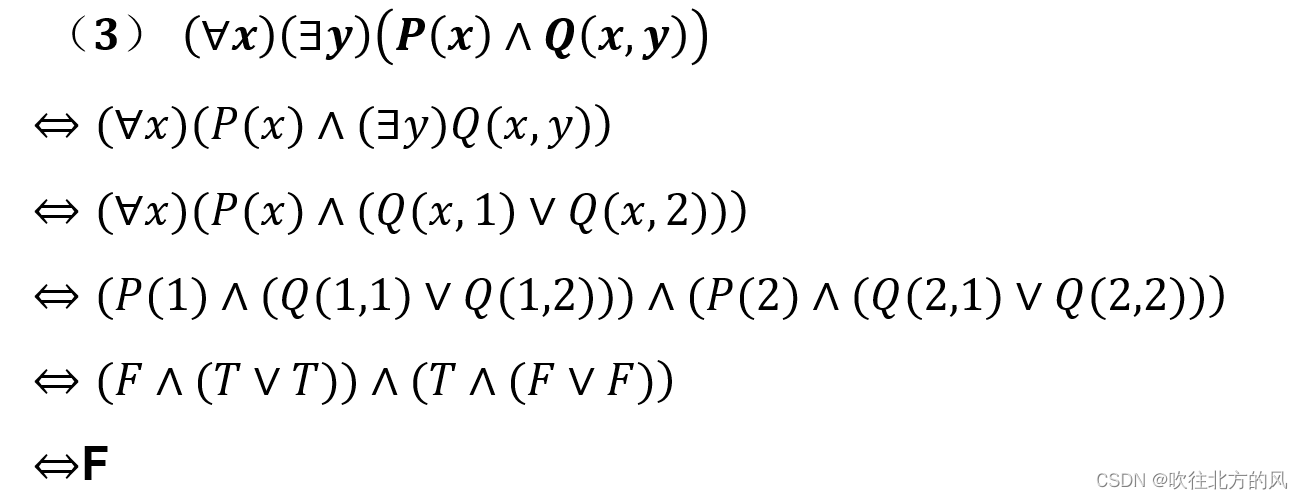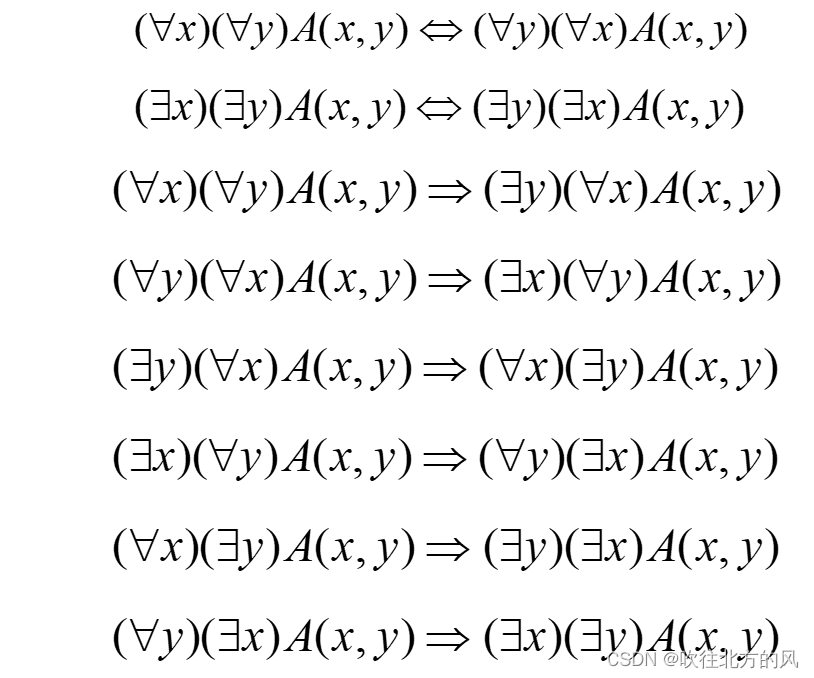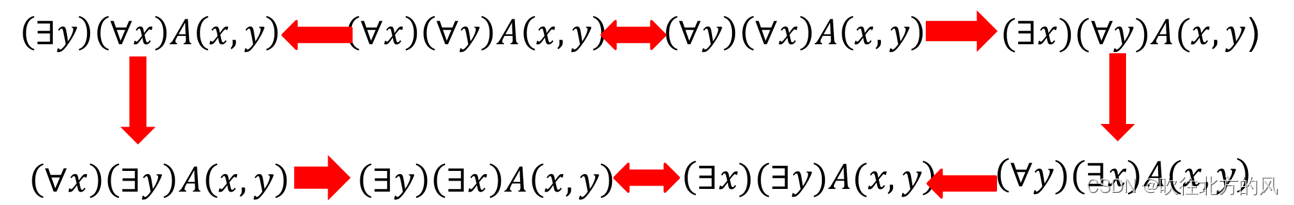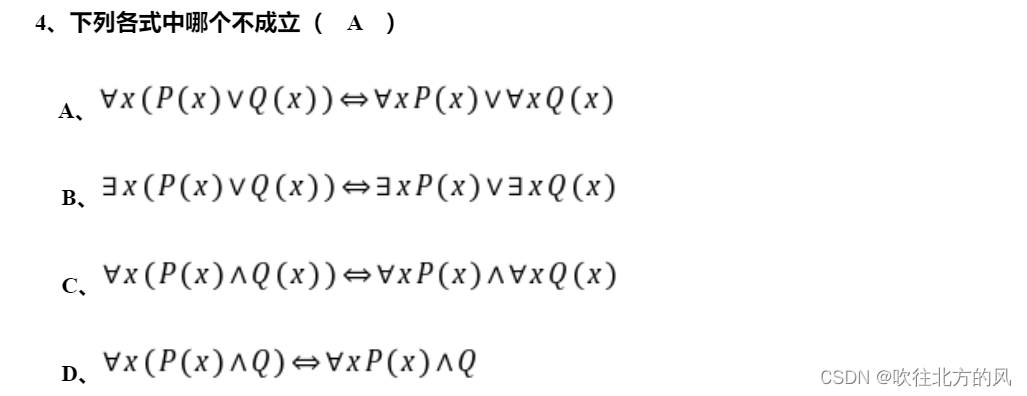当前位置：首页 > news >正文

【离散数学必刷题】谓词逻辑（第二章左孝凌版）刷完包过！

news 2025/8/16 14:46:08

专栏：离散数学必刷题

本章需要掌握的重要知识：

1.利用谓词表达式表示命题

2.变元的约束

3.谓词公式的定义、谓词公式的赋值

4.谓词公式的翻译（注意在全总个体域时使用特性谓词）

5.有限论域上量词的消去

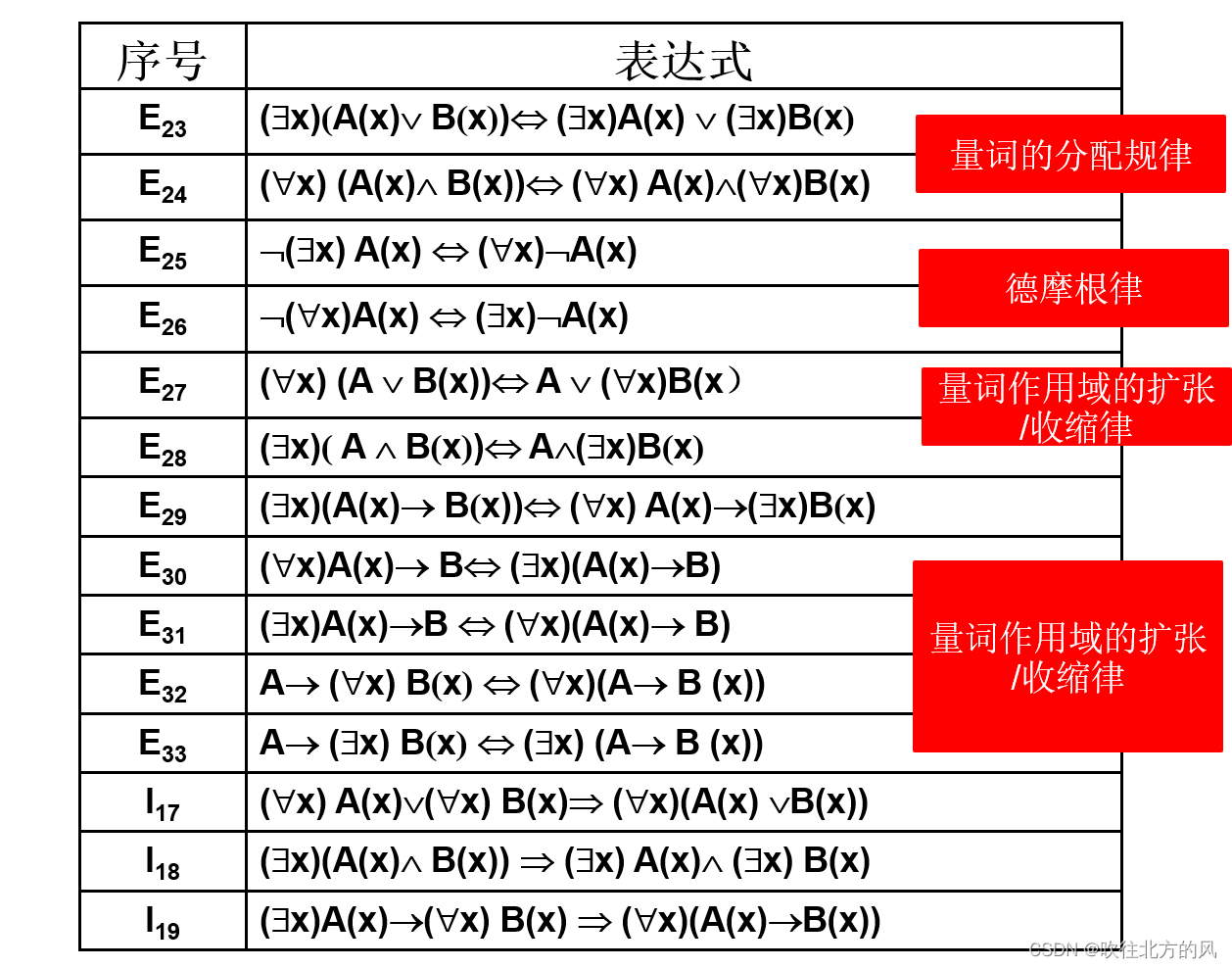
6.谓词公式中关于量词的等价公式和蕴含式（表2-5.1）

7.前束范式前束析取范式前束合取范式

8.谓词推理

8种题型（速通版）：

【1】用谓词表达式写出下面几个命题（都是容易写错的经典例题）：

1、某些大学生运动员是国家选手。

设 S(x) : x 是大学生。 L(x) : x 是运动员。C(x) : x 是国家选手。

则有： $(\exists x)(S(x) \wedge L(x)\wedge C(x))$

2、没有一个国家选手不是健壮的。

设 S(x) ：x 是国家选手。L(x)：x 是健壮的。

则有： $(\forall x)(S(x)\rightarrow L(x))$ 或者 $\rightharpoondown (\exists x)(S(x)\wedge \rightharpoondown L(x))$

3、所有老的国家选手都是运动员。

设 S(x) : x 是国家选手。P(x) : x 是老的。 L(x) : x 是运动员。

则有： $(\forall x)(P(x)\wedge S(x)\rightarrow L(x))$

4、没有一位女同志既是国家选手又是家庭妇女。

设 S(x) : x 是女同志。 P(x) : x 是国家选手。Q(x) : x 是家庭妇女。

则有： $\rightharpoondown (\exists x)(S(x)\wedge P(x)\wedge Q(x))$

5、所有运动员都钦佩某些教练。

设 S(x) : x 是运动员。 P(y) : y 是教练。A(x , y) : x 钦佩 y。

则有： $(\forall x)(S(x)\rightarrow (\exists y)(P(x) \wedge A(x,y)))$

6、有些大学生不钦佩运动员。

设 S(x) : x 是大学生。P(y) : y 是运动员。A(x , y) : x 钦佩 y。

则有： $(\exists x)(S(x)\wedge (\forall y)(P(x)\rightarrow \rightharpoondown A(x,y)))$

【例题】

【2】利用谓词公式翻译下面几个命题：

1、如果有限个数的乘积为零，那么至少有一个因子等于零。

设 N(x) : x 是有限个数的乘积。z(y) : y 等于零。P(x) : x 的乘积为零。F(y) : y 是乘积中的一个因子。

则有： (∀x)( N(x)∧P(x)→(∃y)( F(y)∧z(y) ) )

2、对于每个实数x，存在一个更大的实数y。

设 R(x)：x 是实数。Q(x,y)：y 大于 x 。

则有： (∀x)( R(x)→(∃y)( Q(x,y)∧R(y) ) )

3、存在实数x，y 和 z ，使得x 与 y之和大于 x 与 z 之积。

R(x): x 是实数。G(x,y) : x 大于 y 。

则有：(∃x)(∃y)(∃z)( R(x) ∧ R(y) ∧ R(z) ∧ G(x+y , x⋅z) )。

【3】对下列谓词公式中的约束变元进行换名：
1、(∀x)(∃y)(P(x,z)→Q(y)) $\leftrightarrow$ S(x,y)

则为：(∀u)(∃v)(P(u,z)→Q(v)) $\leftrightarrow$ S(x,y)

2、((∀x)(P(x)→(R(x)∨Q(x)))∧(∃x)R(x))→(∃z)S(x,z)

则为：((∀u)(P(u)→(R(u)∨Q(u)))∧(∃v)R(v))→(∃z)S(x,z)

这里可能有些同学会疑惑了，为什么第2题的 z 变元不换名啊？

首先我们要明确进行约束变元换名的前提：

换名是为了避免出现同一个变量既是约束变元，又是自由变元的情况出现。如果不是这种情况，可以不换。

【4】对下列谓词公式中的自由变元进行代入：

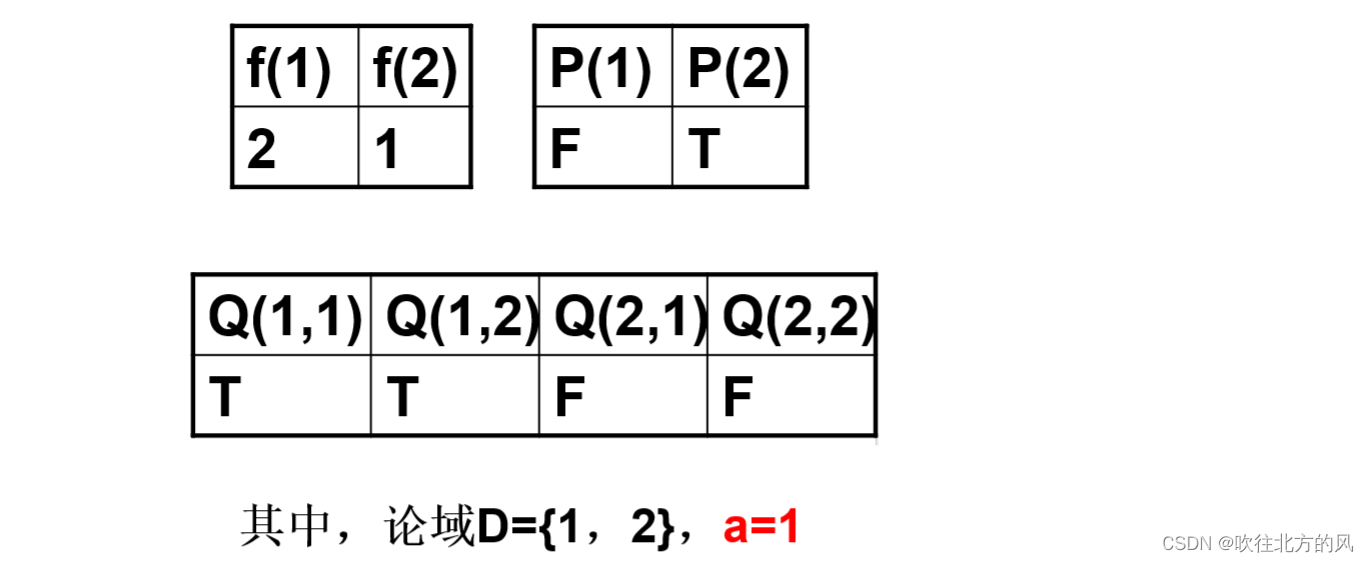
【5】 有限论域消去量词，并对以下公式赋值后求真值：

【6】请记住以下的谓词公式的等价式和蕴含式：

⚠️注意：全称量词与存在量词在公式中出现的次序，不能随意更换。

如果你想记下这个，可以通过如下图辅助性记忆：

用双向箭头表示等价，单向箭头表示蕴含，见它们之间的关系。

【例题】

【7】 求前束合取范式：

前束合取范式的定义：（注意：可以 $l_{1} = l_{2}$ ，也可以 $l_{1} != l_{2}$ ，所以我们只需要简单得满足合取范式、析取范式的结构就可以了，不用满足主合取范式和主析取范式得结构哦！）

前束析取范式定义：

做题时，可能遇到的三种情况：

假设求出的前束合取范式，它的每一个 $A_{ij}$ 都唯一，那么可以采用主合取范式和主析取范式的性质：

求出前束合取范式后，根据第一章主合取范式和主析取范式的知识：

在真值表中,一个公式的真值为T的指派所对应的小项的析取,即为此公式的主析取范式。

那剩下的真值为F的指派所对应的大项的合取,即为此公式的主合取范式。

我们可以直接通过前束合取范式求出前束析取范式：

【例题】

假设求出的前束合取范式，存在有 $A_{ij}$ 不唯一，那么就硬算呗！

例如求：(∀x)(P(x)→Q(x,y))→((∃y)P(y)∧(∃z)Q(y,z)) 它的前束合取范式和前束析取范式

答：先求其前束合取范式

(∀x)(P(x)→Q(x,y))→((∃y)P(y)∧(∃z)Q(y,z))

⇔¬(∀x)(¬P(x)∨Q(x,y))∨((∃y)P(y)∧(∃z)Q(y,z))

⇔(∃x)(P(x)∧¬Q(x,y))∨((∃u)P(u)∧(∃z)Q(y,z))

⇔(∃x)(∃u)(∃z)((P(x)∧¬Q(x,y))∨(P(u)∧Q(y,z)))

我们发现P(x) 和 p(u) ，Q(x,y) 和 Q(y,z)它们的 $A_{ij}$ 不唯一，所以当我们再求出它得前束析取范式时，就只能将其展开，表示前束析取范式：

(∃x)(∃u)(∃z)( (P(x)∨P(u))∧(P(x)∨Q(y,z))∧(¬Q(x,y)∨P(u))∧(¬Q(x,y)∨Q(y,z)))

⚠️注意:

当我们求一个wff的前束合取范式或析取范式时，有些可以直接求出了它的真值（T或F），

例如求：(∃x)P(x)∨(∃x)Q(x))→(∃x)(P(x)∨Q(x))的前束合取范式和前束析取范式

则：

((∃x)P(x)∨(∃x)Q(x))→(∃x)(P(x)∨Q(x))

⇔¬((∃x)P(x)∨(∃x)Q(x))∨(∃x)(P(x)∨Q(x))

⇔¬(∃x)(P(x)∨Q(x))∨(∃x)(P(x)∨Q(x))

⇔T

那么 T 既是前束析取范式，也是前束合取范式，这就是最终结果！！！

我们知道：

单个变元既是简单合取式，又是简单析取式。把T看成简单合取式，它就构成了一个析取范式，类似的，把T 看成一个简单析取式，它就构成了一个合取范式。

因此这是一种特殊的范式。

总之，前束合取范式 <= 前束主合取范式；前束析取范式 <= 前束主析取范式，